Weak adversarial networks for high-dimensional partial differential equations（WAN文献总结）

Weak adversarial networks for high-dimensional partial differential equations

本文讨论如上的文章。

由于基于有限差分和有限元的经典数值方法存在计算缓慢、不稳定和维数灾难的问题。同时因为有限元、有限差分网格点的数量相当于问题的维数d呈指数级快速增加，所以发展基于神经网络的方法。

首先考虑如下具有Dirichlet或者Neumann边界条件的二阶椭圆PDE：

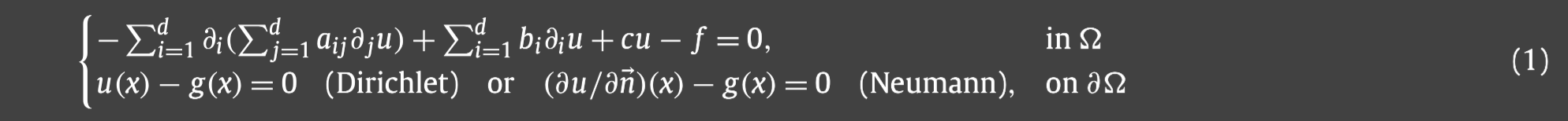
其中：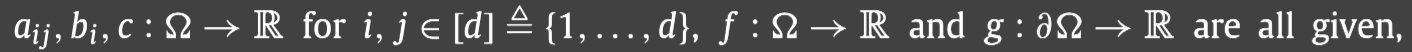

并且椭圆算子具有如下的强椭圆性：存在一个常数$\theta >0$，满足${\xi }^{T}A(x)\xi \ge 0$对于所有的$\xi =({\xi }_1,\cdots ,{\xi }_d)\in {\mathbb{R}}^d$

同时我们也考虑求解如下涉及时间的PDE：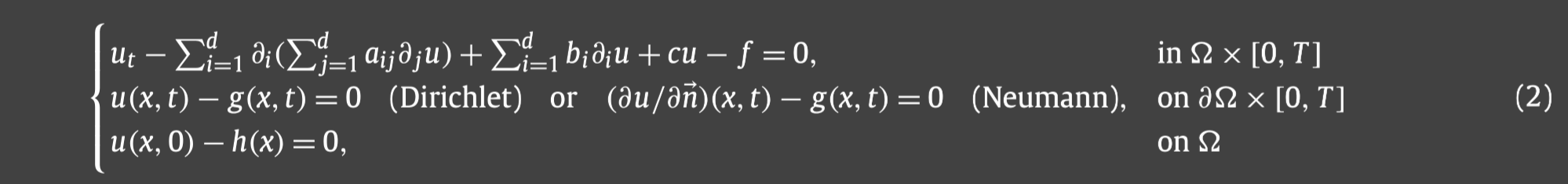

如下将弱解和测试函数分别参数化为原始和对抗神经网络，并采用无监督的形式训练他们，同时在配置点求对应误差。这种方法不需要离散空间，在求解一般高维PDE时快速稳定。同时该方法完全无网格，可以应用于任意形状区域上的PDE.

让我们首先关注边值问题（1）：

在方程（1）两端乘函数$\varphi \in H_0^1(\Omega ;\mathbb{R})$，分部积分得到：

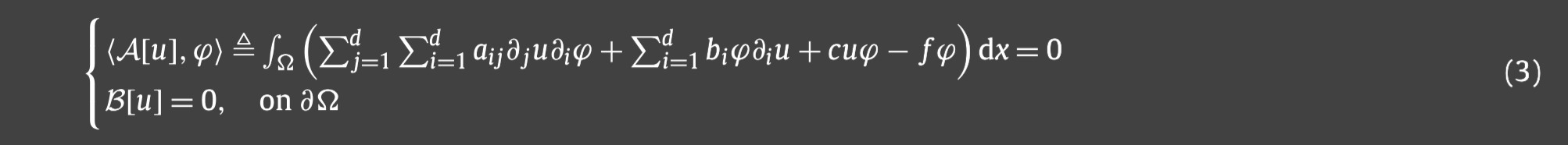
PDE（3）的解就是（1）的弱解，（1）的解称为强解。强解存在的话弱解一定存在，并且两者一定会相等，但弱解存在的话强解不一定存在。

我们可以这么考虑弱解：$\mathcal{A}[u]:H_0^1(\Omega )\to \mathbb{R}$作为一个泛函满足：$\mathcal{A}[u](\varphi ):=<\mathcal{A}[u],\varphi >$，就如（3）中定义的那样。那么泛函$\mathcal{A}[u]$的范数即为（由$L^2$范数诱导）：

所以$u$是（1）的弱解当且仅当$\Vert \mathcal{A}[u]{\Vert }_{op}=0$并且满足边界条件$\mathcal{B}[u]=0$。当$\Vert \mathcal{A}[u]{\Vert }_{op}\ge 0$时，利用弱解，我们可以得到如下的等价推论：

从而可以得到如下的定理：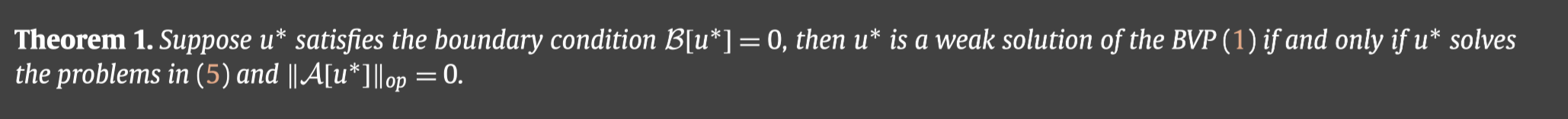

上述定理启发我们，为了得到（1）的弱解，我们可以寻找使得（5）达到最优值的最优解$u$.

同时（5）启发我们寻找函数$u_{\theta }:{\mathbb{R}}^d\to \mathbb{R}$，使得$\Vert \mathcal{A}[u_{\theta }]{\Vert }_{op}$最小，其中$\theta$是待学习的深度神经网络的参数；另一方面，测试函数$\varphi$是一个参数为$\eta$的深度对抗网络，它通过最大化$<\mathcal{A}[u_{\theta }],{\varphi }_{\eta }>$的范数来达到和$u_{\theta }$对抗的目的.

为了训练神经网络神经网络，我们首先需要构建关于$u_{\theta }$和${\varphi }_{\eta }$的目标函数。考虑到对数函数是单调而且严格递增的，所以我们可以重新公式化（5）为：

除此之外，弱解还需要满足（1）中的边界条件$\mathcal{B}[u]=0$，选取边界上$N_b$个配置点，那么Dirichlet边界条件可以刻画为：

同样地，对于Neumann边界条件，可以同样处理.

那么总目标函数就是两个目标（6）和（7）的加权和，为此我们需要寻找一个鞍点来解决如下的这个极小极大问题.

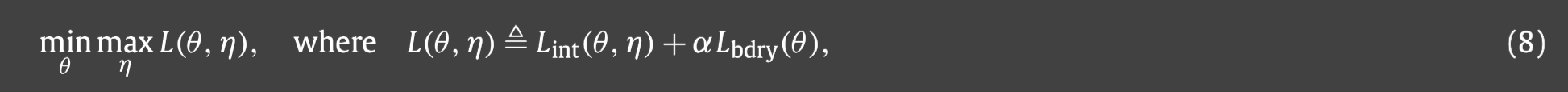
对于给定的目标函数（8），网络训练的关键要素是$L(\theta ,\eta )$关于参数$\theta ,\eta$的梯度，那么$\theta ,\eta$可以通过梯度下降和上升来优化.

为了获得（8）中的$L_{int}$的梯度，我们首先令$<\mathcal{A}[u],\varphi >$的被积函数是$I$，那么可以知道对于二阶椭圆PDE方程（1），$I$的梯度即为：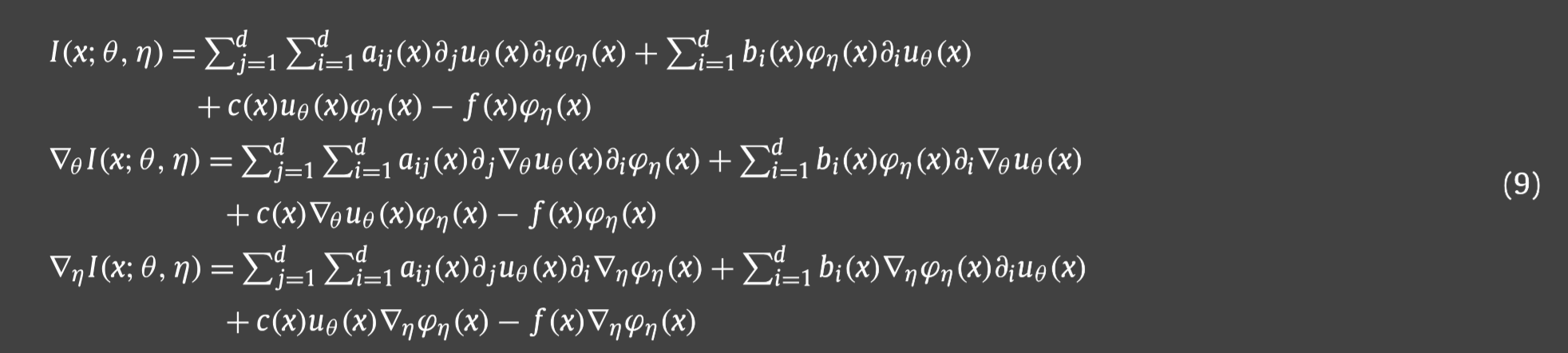

由此我们可以得到$L_{int}$的梯度：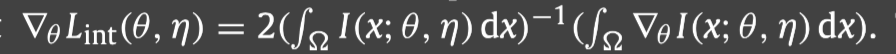

通过随机选取配置点的方法，可以将${\nabla }_{\theta }{L}_{int}$离散。接下去可以应用交替更新来优化参数$\theta$和$\eta$.从而产生如下的算法，称为弱对抗网络(WAN):

我们还可以把WAN扩展到求解具有时间导数的PDE，也即IBVP.如下有两种方法：一种是在时间上采用半离散化，并对每个$t_n$，都是与时间无关的PDE，从而可以迭代求解$u(x,t_n)$，其中算法1可以直接作为求解的子程序；第二种方法是不用任何离散化操作，只是联合处理x和t，并考虑整个区域$\Omega \times [0,T]$的弱解和测试函数.

1.我们首先将[0,T]划分为N等分，然后用有限差分中的CN格式对上面提到的方程（2）中的时间导数进行离散，得到：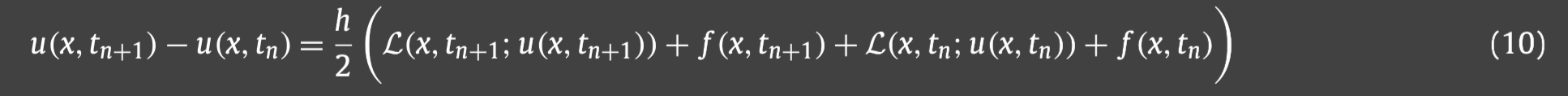

其中：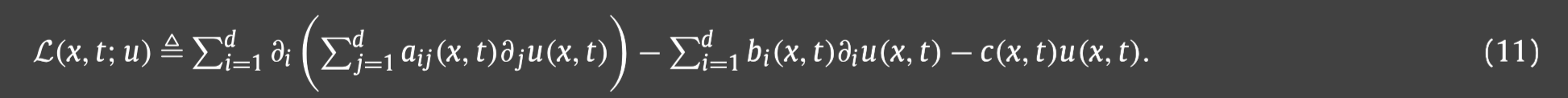

更确切地说，我们以$u(x,t_0)=u(x,0)=h(x)$开始，然后对于n=0，从（10）中求解得到$u(x,t_1)$，由于（10）是关于$u(x,t_1)$的椭圆PDE，所以可以直接应用算法1，得到$u(x,t_1)$作为输出的参数为${\theta }_1$的参数化神经网络$u_{{\theta }_1}(x)$.类似的，我们可以得到$u(x,t_n)=u_{{\theta }_n}(x)$.算法过程如下：

2.第二种需要先得到（2）的弱公式（通过在（2）两边乘以检验函数），得到：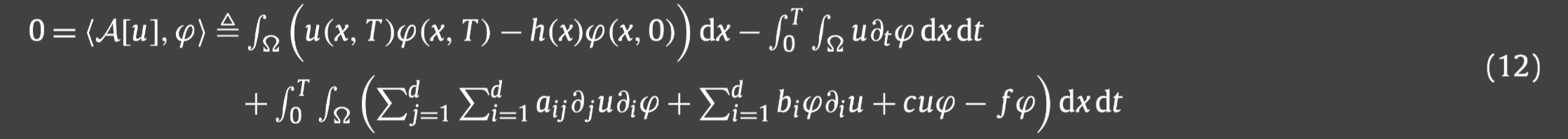

之后我们仿照之前的做法，把弱解$u$和测试函数$\varphi$参数化为深度神经网络$u_{\theta }$和${\varphi }_{\eta }$:$\Omega \times [0,T]\to \mathbb{R}$.同时它的目标函数是：

其中：

对应的算法如下：