我发现了一个问题,之前解释边界的时候使用的双曲线,但是双曲线不存在。后来模糊了,双曲线存在了,但是边界模糊了,我该如何定义边界呢?边界到底是因为什么产生的呢?
按理说从看不见到看得见,这就是边界啊。
首先就是模糊的问题,如何定义模糊。应该把模糊定义为弥散圆到达像曲面S1的时候,超过了检测仪器的规定的大小,但是问题是S1和透镜的距离是可以改变的,透镜的焦距和光圈大小也可以改变,这些都影响最终形成的弥散圆的大小。另一个问题就是就算弥散圆O不超过仪器的规定大小,但是来自物体的光的尺度不同,使得最终看到的物体的微观结构不同,比如是厘米级别,或者毫米级别的。所以弥散圆并不可靠,而是我之前定义的双曲线的长度更合理一些。利用双曲线的长度反应微观结构,渐近线反应视野范围。但是问题是我之前又说过,过多的模糊导致不同的双曲线重叠出现,有没有可能一开始长的双曲线是存在的呢?
我之前无法确定长双曲线的存在,但是现在发现模糊之后,长双曲线很可能是真实存在的。那么我之前提出的简化的版本就是真实的样子,但是还是需要对边界进行讨论。
以双曲线为基线,构造3维的边界。但是这里是在图纸上,我只需要画出2维图形即可。
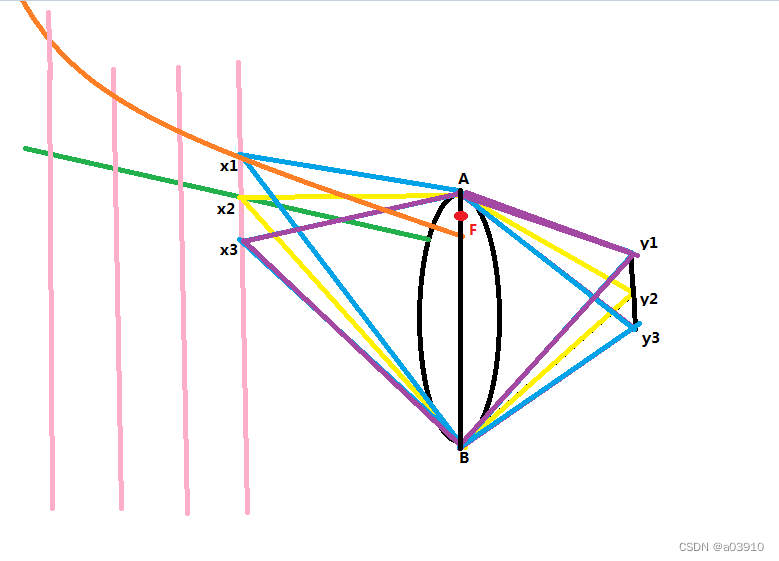
假设x2是边界线上的点,如图所示是绿色,这里我并没有给出双曲线的边界线,因为这里复杂了,我最后直接把整个曲线变形即可得到真实的边界形状了。
x2映射到了y2,y2是像曲面S1的边界,所以紫色的y1就不用看了,因为在成像区域的边界外了。然后是看y3。本来不在边界线上,x1是不可能成像的,因为在视野范围之外了,但是弥散圆存在,使得x1也应该本看做是边界。那么由于这个光程差更大,所以,橙色的双曲线的渐近线斜率更大一些。橙色和绿色包围的区域,设为L1,就是所谓的边界线了。但是绿色并不是真正的边界,还需要把这个区域L1经过一个连续的变换,使得L1的绿色边界变成双曲线,得到的区域L才是真正边界。
但是如果看内部,把y2理解为在成像曲面S1内点,那么也能想象出来内部的形状情况是什么样子的。关键是弥散圆看做是一个成像点,那么整个3维的形状映射为一个点。
但是要这样理解的前提是证明上证明无限长的双曲线存在,还是要做微分方程,我之前就没做。需要证明双曲线,即图中的绿线存在。
现在看另外一个问题。像边界上的不同点,观察的光线的交叉区域的问题,发现a点既在y1上,也在y2上,所以a点在边界上的显示变大了,这符合模糊的说法。
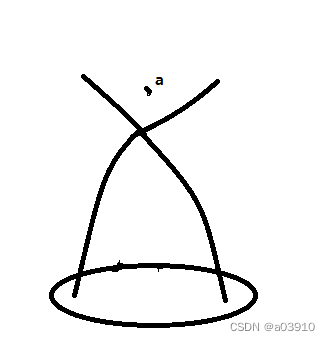
上面的内容错了,并不需要绿色,因为本身就是基于光程差计算的,绿线没有关系,所以不需要根据绿线进行变形,使得绿线成为双曲线,上面的结果就是真实的边界的样子了。
下面是重新建立数学关系的推导。
=========================================================================
模糊本来就是多对多,但是烦人。本来在曲面同胚的时候我解释为位置对应,不管光强,因为光强不重要,不相互干扰就不用管强度了,但是现在强度都相互叠加了,不能不管光强了,所以,除了位置的多对多的关系,还有强度的叠加的关系,我发现模糊的复杂性远超想象。
位置多对多,该怎么考虑呢?我打算从正的多对一,从物空间到像曲面的一个点看。反过来是考虑像曲面的一个局部,找到来自哪个点。问题是任意的局部V都能找到来自物空间的一个点发出的光到达吗?
任意局部不可能,但是充分小的时候,局部V包含于某个弥散圆U中,这是一定的,因为弥散圆的大小是固定的。我想使用有限覆盖定理,那就只能假设弥散圆是开集,像曲面是闭集,这无所谓,因为只是位置的映射关系,不涉及到光强。只要是有限覆盖了,那就有这些集合就有最小的直径,所以只要充分小,就可以包含在一个弥散圆中,那么就能够是物空间中的同一个点发出的光线映射的位置了。
结论就是:对于像曲面上的充分小的局部V都能找到来自物空间的一个点发出的光到达。
所以一对多就完成了定义。
=========================================================================
接着考虑多对一。多对一我之前没有写过,之前是写的等同跟这里不一样。
这里先假设一个前提,就是在模糊的时候,一个点发出的光到达像曲面形成的是区域,而不是线条,这个模糊的区域叫做弥散圆。
我重新开始,先不搞等同,所以多对一是不同位置映射到像曲面S1上的同一个位置,在有弥散圆的情况下。考虑像曲面S1上的一点O, 当O点有个弥散邻域U的时候,U并没有什么用,只是当U出现的时候,其他的点的弥散邻域都是固定大小的。我只能说在O的附近邻域W中,内部的点y1均有弥散邻域U1,只有U1包含O的时候,才能说来自物空间的x1点的光到达了O点,所有的这样的点的弥散圆Ua包含O的时候,通过弥散圆得到物空间的一个点xa,所有xa的集合就是寻找的物空间的区域,对应的多的含义了。
完成了多对多的拆分,再深入考虑他们。(这只是我的一种拆分的方式,但是还有更多的,我只是随便写写的。)
=========================================================================
但是要想得到完整的描述多对多的关系,只能使用集合族映射了,就是比如{x1,x2,x3}->{y1}, {x1, x3}->{y2}, 这种样子。多对一改成是集合族A到曲面S1的一一映射,集合族A的元素是物空间D的子集,但是子集之间是可以相交的。
一对多改成是物空间D到集合族B的一一映射,集合族B的元素是像曲面S1的子集,但是是重复的。
这样我把多对多写成两个单独的映射了。问题是这两个映射连续吗?就算是不连续,也要赋予使其连续的拓扑结构,那就认为是连续的, 其实是同胚的。
我这里没写清楚解析的过程,我再写一下。我这里的定义是非构造性的,因为充分小不知道多小。只要邻域的直径是一定长度,它就有直径无限小的内部,也算。但是在有限覆盖的情况下,这不是问题,这是点集拓扑中的紧致空间。
取所有的像S1的充分小的邻域构成集合族B。
H1:D->B作为一一映射,感觉并没有包含所有的一对多的情况,比如a->y, b->y, 只选择了其中的一个。
然后是J1:A->S1作为一一映射,这个也漏掉了一种情况,比如集合a映射到y, 集合b->y, 但是假设b是a的真子集,而A根据定义,是所有映射到y的物点x的集合,那么集合b就不属于A了。
这两个映射看起来是有问题的。首先我想要找的是等价原来的多对多的映射关系。考虑H1的a->{y}, b->{y}, 只选择了其中的一个的情况,这种情况确实存在,但是要注意,我前面加了所有,也就是说,还有这种情况b->{y, y1}, a->{y, y2}。漏掉的情况可以通过取子集族然后把{y,y1}和{y,y2}等同补全。就不会有遗漏。发现写错了,H1不是映射,而是关系,只有改成关系才合理。倒过来写成多对一也行,但是还不如学J1的定义。
J1看起来也是存在遗漏的情形。但是既然b是a的真子集,那么b的像点就是a的像点,又何必非要构建以b为变量值的映射找b的像点呢。
由于H1在讨论的过程发生了矛盾,重写一遍定义一对多:
由于对于像曲面上的充分小的局部V都能找到来自物空间的一个点发出的光到达。那么取极大的局部V存在来自物空间的一个点发光到达。这个对应关系是一对一的,不可能这点发出的光到达其他的位置,不在这个局部上了。所有这样的极大局部V组成像曲面S1的集合族B。
这样,H1:D->B是一一映射。
总之,这两个映射都是一一对应的,还是微分同胚的,而且要从像区域S1得到物区域D选择J1还是选择H1呢?这两个映射都没有问题,使用H1,需要把像区域S1使用覆盖的观点。使用J1是逐个点求原象。(怎么说呢?我本来是想建立拆分的方式,使得每个映射不能完全表述多对多的关系的,只有合起来看的时候能清晰表述。但是发现拆分失败了,H1和H2都能完全表述这种关系,这意味着问题虽然从多对多变成了新的拓扑空间的微分同胚,但是并没有得到简化。)
=========================================================================
虽然建立了数学上的描述,但是我一开始假设的都是点和单连通区域(集合族的元素都是单连通区域)的一一对应,为什么元素不可以是非单连通的呢?当然可以,只要透镜改造一下,就可以得到各种连通性的区域了,这就更复杂了,我连位置都没搞明白,不管这个。
所以像曲面上的点的关系,其实就是物体空间D上的另一种关系。更具体地说,在像曲面上给出一条直线求斜率,在物体空间表现为什么呢?只能把物体空间分割成不同的区域,并且分割的区域还是重叠的,虽然是重叠,但是需要重新规定拓扑结构,使得在欧式空间中看起来是重叠的,但是在新的拓扑空间中不是,然后就可以定义这个拓扑空间的微分运算和积分运算,所以知道斜率在这个拓扑空间中表示什么了吧,很难想象,但是这就是微分流形。
=========================================================================
现在考虑弥散圆内的等同到底是等同了什么,如果把像曲面S1限制在一个弥散圆内,那么在物空间中也是有了限制,但是还是多对多的关系。根据上面的定义那么假设是y的弥散圆O,那么就是物空间中的任意点x, 映射成区域U和O的交集不为空,那么可以理解为等同的是集合族中,所有元素包含这样的x的元素取并集了?或者理解为由符合上面的x组成的元素作为物空间D的子集呢?
这里有两种理解方式,第一种是多对一和一对多拆解得到的,第二种直接是多对多,当两种表述方式完全等价的时候,那么这两种理解方式也是一个结果。
=========================================================================
为了在弥散圆内准确理解像曲面上的关系,只能把物体空间分割成不同的小块,而且还重叠了,重新给了拓扑结构。(但这是多对一理解像。从像理解物体空间选择一对多。需要把像曲面分割,不管这个。)然而这只是弥散圆存在的时候的拓扑结构,并没有做等同,当做了等同之后,重叠的拓扑空间的元素中的部分有相同的会合并了(注意是部分,而不是全部),使得合并之后与弥散圆一对一对应,这是从多对一的值域进行了分割,还是重叠分割,利用一对多的方式。
所以弥散圆的等同处理,更加的复杂了。
确切地说,就是分割了物体区域D和像曲面S1, 分割方式是有重叠的,这个子集分别形成了各自的拓扑空间,然后他们之间的关系是同胚的。这样我解释了什么是等同。
=========================================================================
我上面给出了弥散圆存在的情况下,拓扑空间的建立,并且给出了还是同胚关系。但是这个建立过程是建立在完全清晰成像的说法上的,即是像区域的弥散圆的最大直径没有超过测量仪器的。
这样就能解释明明是清晰成像,为什么没有得到微观结构的信息。因为分割区域的大小决定了观察的尺寸(在像中的一个点代表的空间的一大块区域)。高清成像不代表是有成像微观结构。高清和微观是两回事。
========================================================================
我本来是要再写光强的叠加问题的,但是我发现我自己建立了新的微分同胚,那么就不需要在考虑光强了,因为是一一对应的,即使光强叠加模糊了像曲面上的每个点,但是每个点存在邻域U和物体的区域D是一一对应的,也就是说测量仪器看到的不是点,而是这个邻域U,测量仪器看到的是我上面推导的拓扑空间,而不是成像曲面S1,当把邻域U看做是一个点的时候,就会明白光强模糊微观结构(即U的内部的光强叠加)没有意义了,因为测量仪器本来也看不到微观结构。这个时候,测量仪器认为测量得到的是这个尺度下的最高清了,没有更清晰的可能了,因为测量仪器只能测量这个尺度。
========================================================================
好吧,结束了,不能说没有解决问题,但是没有得到我想要的结果。(我更想了解一个问题,如果只能看到1厘米的倍数的结构,有一天得到了1.1cm的尺子,不是测出来的,而是假设知道的,能否测量出来1厘米以下的结构呢?因为0.1cm看不出来,但是十个尺子紧密排列得到了11cm就能够看出来多出了1cm。问题是0.9cm看不到如何人为的排列?不能主动排列,只能无意中的排列就能观察到了,只要观察到一次,就可以人为的多观察几次,然后获得规律,利用规律排列,虽然不是人为的主动排列,但是在规律中能找到更大几率观察到。把所有的观察的结果分析,就能得出0.9cm是0.9cm了。所以想要分析微观结构,尽管从弥散圆来说已经等同看不出来了,但是在更大的区域中,存在大量的反常光学现象,可以拼凑出来小于弥散圆尺寸的成像,这需要大量的数据计算才能得到。弥散圆并没有让微观信息消失,而是分散了在广大的区域中。)





















 168
168

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








