python计算Friedman排名代码
首先先说输入数据,为了迅速处理,采用csv格式的表格,读者可以先理解这里提供的示例和代码,再自行调整
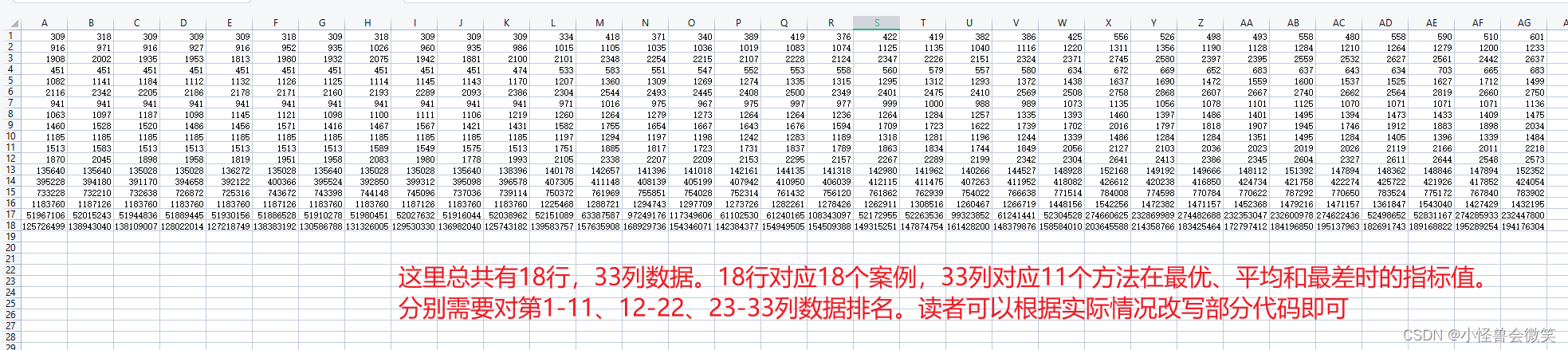
下面是代码,代码会生成一个排名文件Rank.csv。其除了会生成每个方法再每个案例下排名,还会得到一行平均排名,故最后生成的形状为19*33
# -*- coding: utf-8 -*-
"""
Created on Tue Aug 9 10:15:36 2022
@author: Administrator
"""
import numpy as np
da=np.loadtxt("values.csv",delimiter=",",dtype="str")#np.float32
n=11 #n是11个方法进行排名
#[bpd,apd,wpd]分别是最优,平均和最差指标值
bpd=da[:,:n]
apd=da[:,n:n+n]
wpd=da[:,n+n:]
all_pd=[bpd,apd,wpd]
all_pd1=[]
#如果不需要最优,平均和最差指标值分别计算,可以去掉这个for循环直接用da
for pd in all_pd:
pd=pd.tolist()
pd1=[]
for x in pd:
x1=[float(i) for i in x]
rank1=1
used=0
minn=1000000000000
same_l=[]
x2=[0 for _ in range(n)]
while used<n:
# print(used)
for j in range(0,n):
if x2[j]==0:
item=x1[j]
if item<minn:
minn=item
same_l=[]
same_l.append(j)
elif item==minn:
same_l.append(j)
if len(same_l)==1:
avg_pd=rank1
else:
avg_pd=rank1+(len(same_l)-1)/2
for j in same_l:
x2[j]=avg_pd
rank1=len(same_l)+rank1
used=used+len(same_l)
same_l=[]
minn=1000000000000
pd1.append(np.array(x2))
pd=pd1
all_pd1.append(np.array(pd))
all_pd1=np.array(all_pd1)
tmp=np.hstack((all_pd1[1],all_pd1[2]))
all_pd1=np.hstack((all_pd1[0],tmp))
tmp=np.mean(all_pd1,axis=0)
tmp=tmp.reshape((1,n*3))
all_pd1=np.vstack((all_pd1,tmp))
np.savetxt("ranks.csv",all_pd1,delimiter=",",fmt="%.3f")

























 8158
8158

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










