定位，用最通俗易懂的方法2：TDOA与对应的CRLB

原创已于 2025-01-22 15:04:18 修改 · 1.3k 阅读

38 ·

CC 4.0 BY-SA版权

文章标签：

#TDOA #CRLB #定位

于 2025-01-10 21:20:03 首次发布

二郎就不设置什么VIP可见啥的了，这样大家都能看到。
如果觉得受益，可以给予一些打赏，也算对原创的一些鼓励，谢谢。
钱的用途：1）布施给他人；2）二郎会有更多空闲时间写教程

起因：

二郎虽然也对TDOA和CRLB有所了解，而且写了一些相关的代码，但是还是觉得不够透彻，不能非常好地去教给别人，所以，本专题，二郎就用代码和解释并行，一步一步和大家说明，公式是怎么代码实现的，以及怎么仿真的。
论文《A Simple and Efficient Estimator for Hyperbolic Location》

仿真：

1）初始配置

clc; close all; clear all; warning off;  % 程序初始化。
L = 10e3;                               % 蒙特卡洛运行次数。            
randn('seed',0);                        % 初始化随机数生成器。

uo = [-50 250]';                        % 真实源位置。

x = [0 -5 4 -2 7 -7 2 -4 3 1];          % 真实传感器位置矩阵。
y = [0 8 6 4 3 5 5 2 3 8];
S = [x; y];

M = size(S,2);                          % 传感器数量。
N = size(S,1);                          % 定位维度。

ro = sqrt(sum((uo*ones(1,M)-S).^2))';   % 真实源-传感器的距离
rdo = ro(2:end)-ro(1);                  % 距离差，其他距离与第一个距离的差

R = (eye(M-1)+ones(M-1))/2;             % TDOA 的协方差结构

论文对应：
1）距离差
在这里插入图片描述

2）协方差结构
论文原文
在这里插入图片描述
matlab运行结果

2）噪声变化配置

NsePwrVecdB = -60:4:-24;                % 改变测量噪声水平

fprintf('模拟进行中');
for nseIdx = 1:length(NsePwrVecdB),     % 改变测量噪声水平
    fprintf('。');
    nsePwr = 10^(NsePwrVecdB(nseIdx)/10);
    Q = nsePwr * R;                     % TDOA（范围差）噪声的协方差矩阵

在这里插入图片描述

这里Q = nsePwr * R; 是噪声的线性功率值乘以单位协方差矩阵，构建出实际的协方差矩阵。

3）CRLB

crlb(nseIdx) = trace(TDOALocCRLB(S,uo,Q));

用迹是把x，y，z方向的误差方差相加

function [CRLB] = TDOALocCRLB(SensorPositions, SourceLocation, Q)
% SensorPositions: (Dim x M) 矩阵，每一列是一个传感器的位置，第一列是参考传感器
% SourceLocation: (Dim x 1) 源位置
% Q:              TDOA（范围差）向量的协方差矩阵
% CRLB:           (Dim x Dim) 估计源定位的 CRLB 矩阵

% 通过输入我们就能看出，求CRLB是和传感器位置、源位置、协方差矩阵有关的

M = length(Q) + 1;

if (M < size(SensorPositions, 1) + 2)
    fprintf('传感器数量至少应为 %d\n', size(SensorPositions, 1) + 2);
    return;
end;

if (rank(SensorPositions) < size(SensorPositions, 1))
    disp('传感器不应位于同一平面或直线上！');
    return;
end

S = SensorPositions; 
u = SourceLocation;

M = size(SensorPositions, 2);
ro = sqrt(sum((u * ones(1, M) - S).^2)); %传感器和声源的距离

d_u = (S(:, 2:end) - u * ones(1, M - 1))' ./ (ro(2:end)' * ones(1, size(S, 1))) ...
      - ones(M - 1, 1) * ((S(:, 1) - u)' / ro(1));

J = d_u' * inv(Q) * d_u;    % FIM
CRLB = inv(J);

论文对应：
1）Gt

d_u = (S(:, 2:end) - u * ones(1, M - 1))' ./ (ro(2:end)' * ones(1, size(S, 1))) ...
      - ones(M - 1, 1) * ((S(:, 1) - u)' / ro(1));

在这里插入图片描述
对应-Gt，这个负号其实没关系，因为有两个，相当于负负得正，还是一样的。
2）公式求解
c是信号传播速度，由于使用的r，不涉及速度，因此c=1。

J = d_u' * inv(Q) * d_u;    % FIM
CRLB = inv(J);

在这里插入图片描述

我们这里再重新体验一遍CRLB的推导过程

①构建测量值的似然函数，这里测量值是r
在这里插入图片描述

一般情况下会转换成对数函数，方便求解

这里也涉及求导，两数相乘，前导后不导加上后导前不导

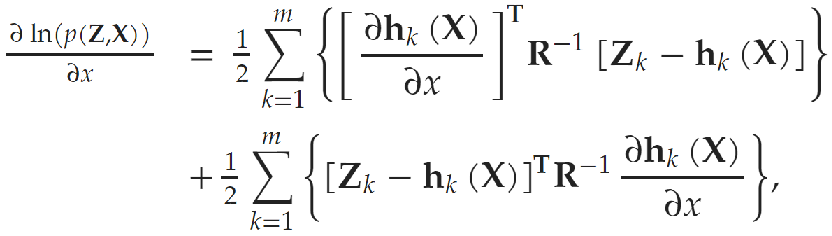
二阶导也是一样

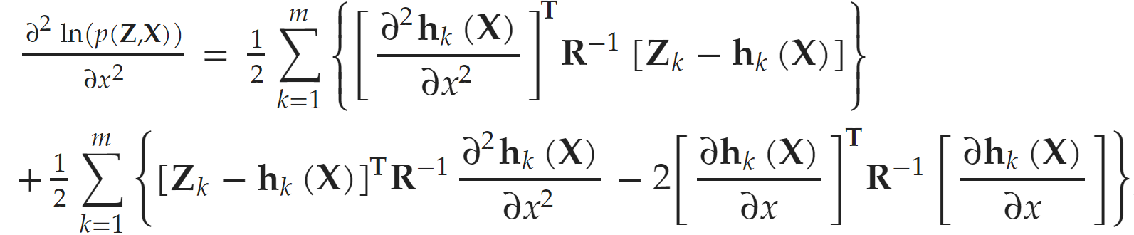
这里还有个关键点就是求期望，Zk的期望等于hk
因此

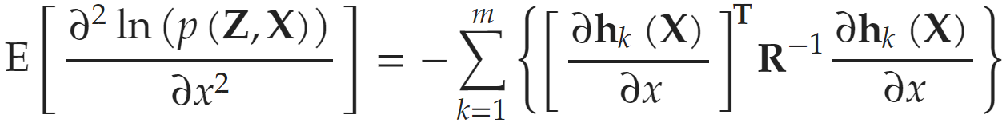
②对对数似然函数进行求导
在这里插入图片描述
Fisher 信息矩阵是一个 n×n 矩阵（n个带噪声的测量值），其元素由对数似然函数的二阶偏导数的期望值组成。

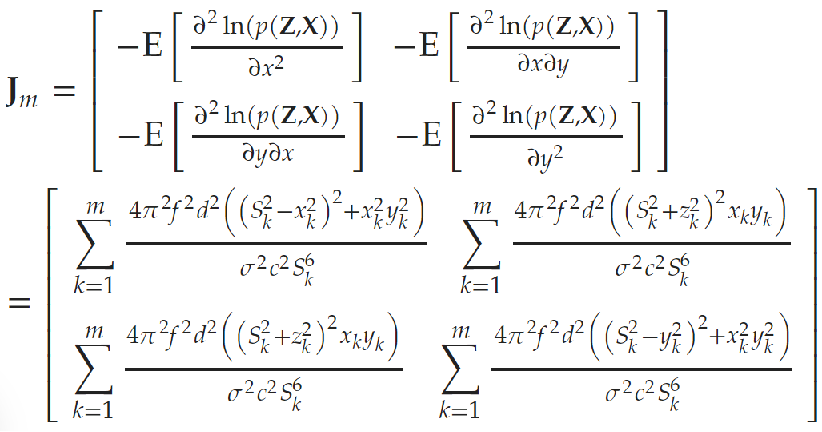
③构建zp的CRLB，对数似然函数的求导的积求期望

在这里插入图片描述
④得到FIR函数的形式后求逆，得到CRLB

4）求TDOA的过程---蒙特卡洛

SimulationMSE = 0;
for k = 1 : L,                     					% 蒙特卡洛模拟。
    rdNse = sqrt(nsePwr/2) * randn(M,1);
    rd = rdo + rdNse(2:end)-rdNse(1);   			% 噪声源 TDOAs（范围差）。
    u = TDOALoc(S,rd,Q);
    SimulationMSE = SimulationMSE + norm(u-uo,2)^2; %多次计算的误差平方累加
end;
mse(nseIdx) = SimulationMSE/L;

$S_i = (x_i - x_0)^2+(y_i - y_0)^2$
$result = (S_1+S_2+……+S_n)/N$

5）求TDOA的过程---两步法---第一步 ---认为x，y和r无关

function [SourceLocation] = TDOALoc(S, r, Q)
% S:        (Dim x M) 矩阵，每一列是一个传感器的位置，第一列是参考传感器，M 是传感器的数量，至少应为 Dim+2
% r:        (M-1) x 1 的 TDOA 测量值乘以信号传播速度
% Q:        r 向量的协方差矩阵
% SourceLocation: 估计的源位置

RptCnt = 1;     % 第一阶段重新计算 W1 的重复次数

M = length(r) + 1;

R = sqrt(sum(S.^2))';

%=========== 构建相关向量和矩阵 ============
h1 = r.^2 - R(2:end).^2 + R(1)^2;
G1 = -2 * [S(:, 2:end)' - ones(M-1, 1) * S(:, 1)', r];

%============= 第一阶段 ===================================  
B = eye(M-1);
W1 = inv(B * Q * B');
u1 = inv(G1' * W1 * G1) * G1' * W1 * h1;

for j = 1:max(1, RptCnt),
    ri_hat = sqrt(sum((S - u1(1:end-1) * ones(1, M)).^2));
    B = 2 * diag(ri_hat(2:M));  
    W1 = inv(B * Q * B');
    u1 = inv(G1' * W1 * G1) * G1' * W1 * h1;
end

u1p = u1 - [S(:, 1); 0];

程序对应
1）构建相关向量和矩阵

%=========== 构建相关向量和矩阵 ============
h1 = r.^2 - R(2:end).^2 + R(1)^2;
G1 = -2 * [S(:, 2:end)' - ones(M-1, 1) * S(:, 1)', r];

在这里插入图片描述

在这里插入图片描述

2）初始迭代

B = eye(M-1);
W1 = inv(B * Q * B');
u1 = inv(G1' * W1 * G1) * G1' * W1 * h1;

在这里插入图片描述

这是初始迭代，我们的权重设置的是对角线矩阵，也就是第一次只和协方差矩阵有关

3）获得初始的u1，然后完成权重的获取

for j = 1:max(1, RptCnt),
    ri_hat = sqrt(sum((S - u1(1:end-1) * ones(1, M)).^2));
    B = 2 * diag(ri_hat(2:M));  
    W1 = inv(B * Q * B');
    u1 = inv(G1' * W1 * G1) * G1' * W1 * h1;
end

这里有点差别，它没有用 $r_{i1}$ ，而是直接用声源的 $x$ 和 $y$ ，获得距离，进而按照距离进行加权
在这里插入图片描述

6）求TDOA的过程---两步法---第二步---弥补第一步无关引入的误差

1）定位结果计算的距离，应该等于计算的距离

u1p = u1 - [S(:, 1); 0];
%========== 第二阶段 =====================================
h2 = u1p.^2;
G2 = [eye(length(u1p) - 1); ones(1, length(u1p) - 1)];
    
B2 = 2 * diag(u1p);
W2 = inv(B2') * (G1' * W1 * G1) * inv(B2);
u2 = inv(G2' * W2 * G2) * G2' * W2 * h2;

在这里插入图片描述

在这里插入图片描述

计算出来的结果是平方的形式，需要利用之前求的结果，给出正负号

%=========== 映射 ========================================
SourceLocation = sign(diag(u1p(1:length(u2)))) * sqrt(abs(u2)) + S(:, 1);
%============================================================

至此，完成了求解，之后可以展示结果

结果展示：

    mse(nseIdx) = SimulationMSE/L;
end;
fprintf('\n');

% 绘制结果。
figure(1); plot(NsePwrVecdB/2,10*log10(mse),'xk','MarkerSize',8); hold on;
plot(NsePwrVecdB/2,10*log10(crlb),'k'); grid on; hold off;

xlabel('10 log(c\sigma)'); 
ylabel('10 log(MSE)');
legend('新方法','CRLB');
ylim([0 60]);

在这里插入图片描述