最近在学习自抗扰控制,学习自抗扰的时候,就不得不先复习一下PID,并进行对比,在重新学习PID的时候,就不能仅仅停留于PID是如何调试的,PID各个参数怎么用。应该更深一层,深入到控制理论中,确实对我帮助较大,大致能够解释PID如何使系统稳定,并且从算法原理的角度解释PID为何应用广泛。下面是我个人的一些理解与笔记:
比例环节
假设被控对象是一个一阶惯性系统,其传递函数可以表示为:
G = 1 / (s + a)
转换为状态方程为:
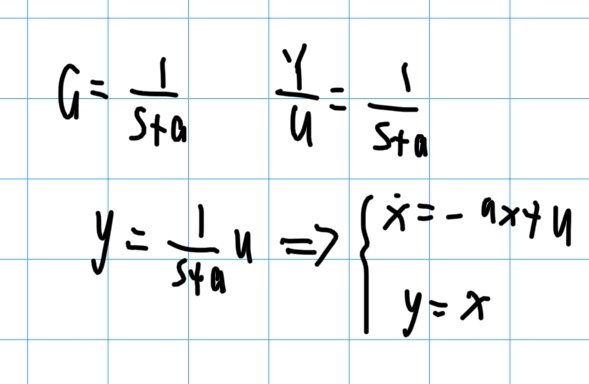
假设我们的控制目标记作v,则纯比例环节的话,框图可以简化为以下,并且我们可以化简一下上述的微分方程:
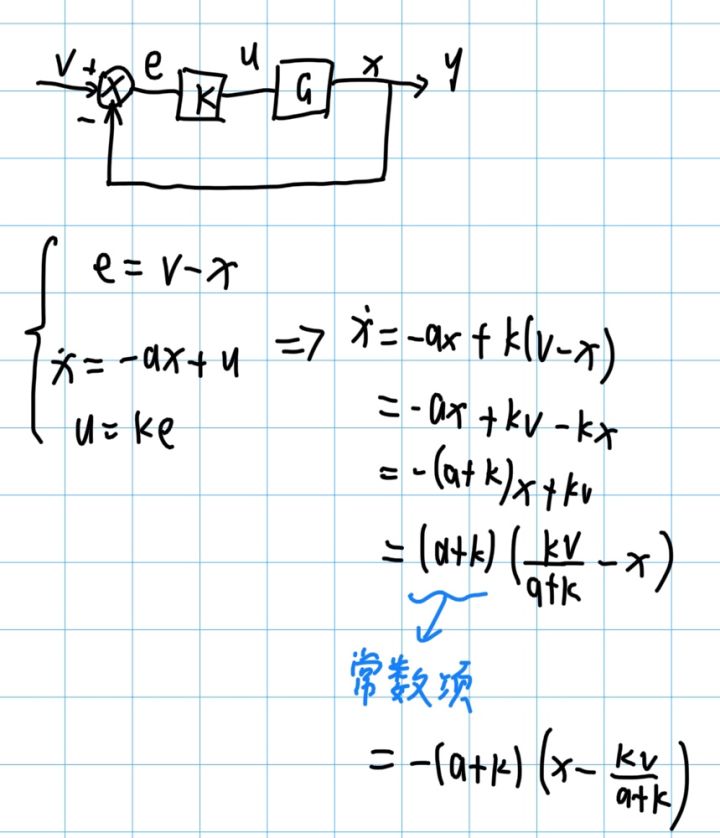
之后可以将非常数项单独拉出,定义为另一个变量 z = x - kv/(a+k):

之后可以根据此微分方程,求解出时域的表达式,根据时域的表达式,便可以得到其稳定条件:

由上可知,k+a > 0 即为其稳定条件,这个k 其实就是 PID 中的 Kp,理论上 k 足够大的话,就可以满足大部分的一阶系统,并使其稳定。当然,如果是纯p环节的话,就会有稳态误差,可以继续求极限得到:

从稳态误差的结果来看,只要系统的系数 a≠0 ,纯P环节的话,会一直存在一个稳态误差。
PI环节
为了弥补比例环节的缺陷,引入累计误差的概念,即PI控制:
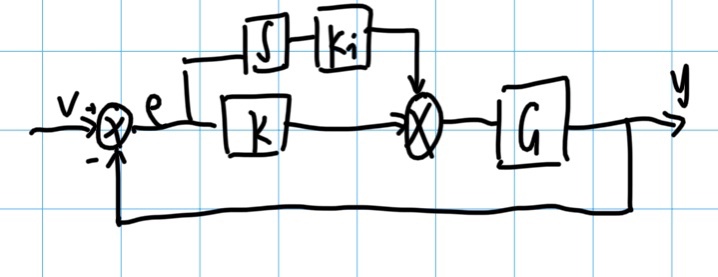
则系统的状态方程就可以写为:
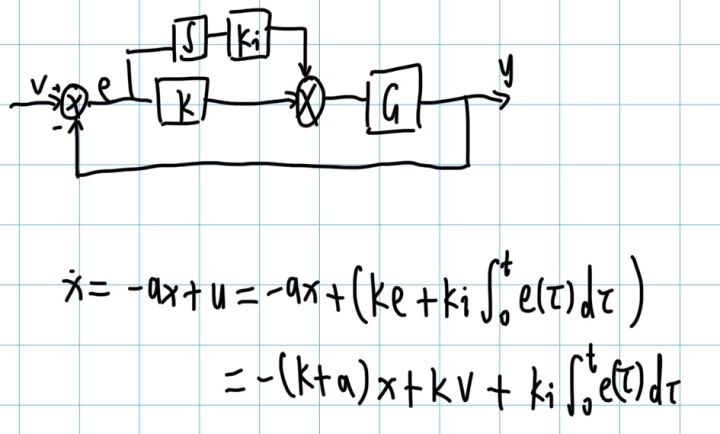
这样上述积分的写法比较麻烦,可以用一个变量 e0 来代替,之后就可以方便化简:

化简到此步的时候,可以将与 Ki 相乘的变量再记作一个新的变量 e1 = e0 - a * v / ki,之后继续化简:
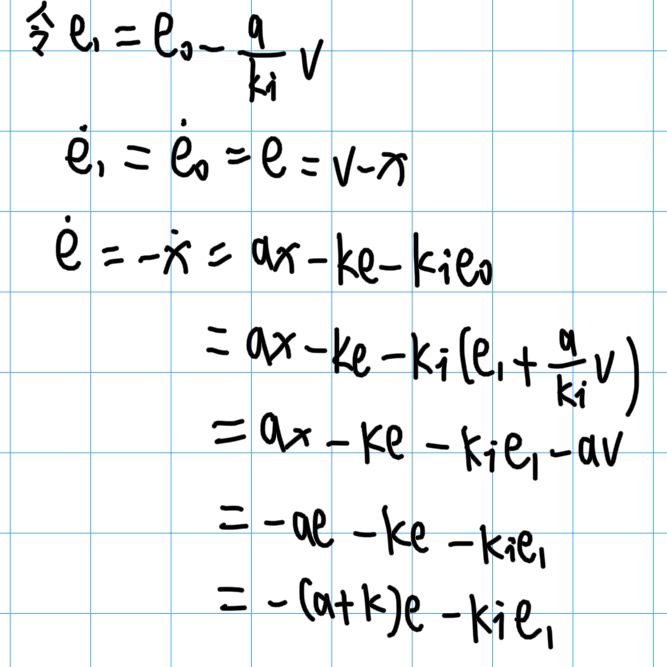
根据此微分方程,可以得出此系统的稳定条件:


根据稳定条件以及最终系统状态的稳定后状态,可以得出最终系统会趋向于当前误差e趋向于0,误差积分会趋向于 a*v/ki,不同的系统对于PI控制器来说,满足了稳定条件后,最终误差都会趋向于0,不同的系统不一样的是误差积分。
PID控制器
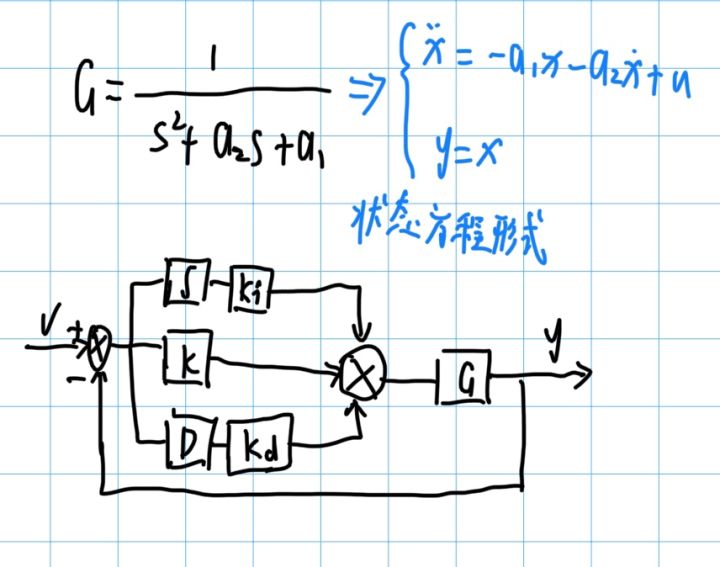
上述是以一阶系统来分析,假如有一个二阶系统,二阶系统的传递函数可以简化为:
G = 1/(s^2 + a2*s + a1)
可以给出PID的简易框图:
根据此框图,可以化简出关于误差e的微分方程:
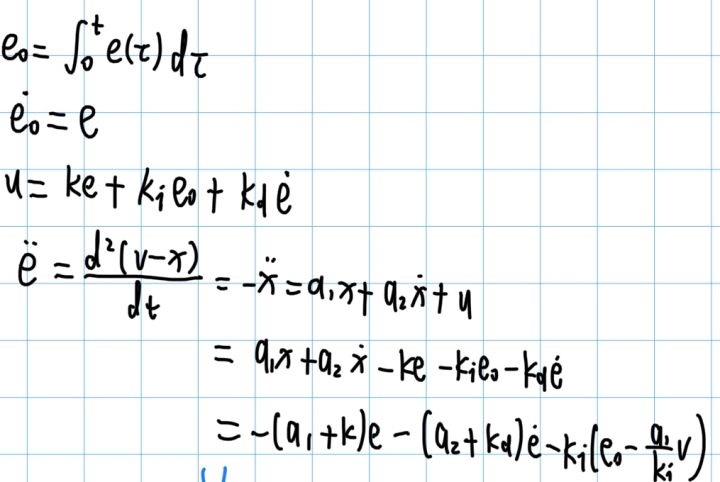
将 e0 与 e 看作是两个新的状态,可以得到一个新的微分方程组:

两边同时求微分,可以将 e0 消去,得到一个关于 e 的三阶微分方程:
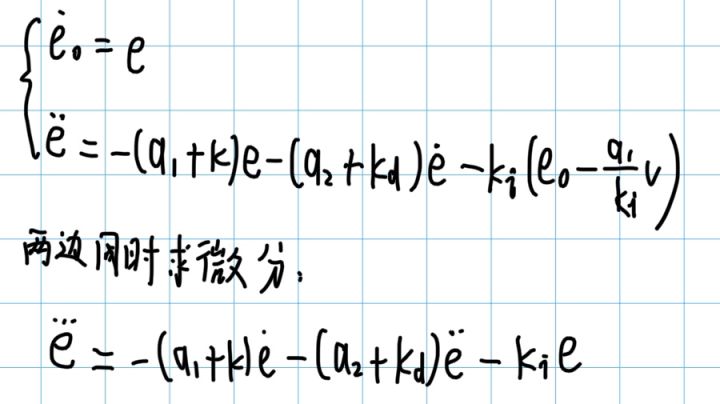
之后可以根据三阶线性定常系统的稳定条件,得出各系数的范围:

此时三阶系统不同与之前的一阶系统的条件那么容易得到,我们可以借助劳斯判据来得到稳定条件:

总结
根据上述劳斯判据得到的稳定条件,我们可以得到,理论上 k,kd参数足够大,并且 ki 大于0的情况下,一阶,二阶系统都可以使用PID算法使其稳定,并消除稳态误差,而大多数实际应用的系统即为一阶与二阶系统组成,一方面PID算法简单易懂,容易实现,另一方面,本文从PID算法的原理进行分析,从原理上就可以看出PID算法确实适合大部分的实际系统,也是其能够应用广泛的深层原因。























 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








