反步设计法是一种递归设计方法。它的主要思想是通过递归地构造闭环系统的Lyapunov函数获得反馈控制器,选取控制律使得Lyapunov函数沿闭环系统轨迹的导数具有某种性能,保证闭环系统轨迹的有界性和收敛到平衡点,所选取的控制律就是系统镇定问题、跟踪问题、干扰抑制问题或者几种问题综合的解。反步设计方法既适用于线性系统也适用于非线性系统,因此该方法一经提出,便受到广泛关注。
一、反步法控制器设计
控制目标:
寻找反馈控制律 以及李雅普诺夫函数
以及李雅普诺夫函数 使得原点
使得原点 为全局渐进稳定的平衡点。
为全局渐进稳定的平衡点。
(1) 定义第一阶子系统的李雅普诺夫函数
,
求导:
(2)
设计期望的状态变量形式
,
令其为虚拟控制
,
并定义误差:
(3)
得到第一阶子系统状态的稳定项
Simulink模块搭建:

结果分析:
在反馈控制律 u
以及李雅普诺夫函数  的影响下,原点
的影响下,原点  为全局渐
为全局渐
进稳定的平衡点,系统 输出结果:
输出结果:
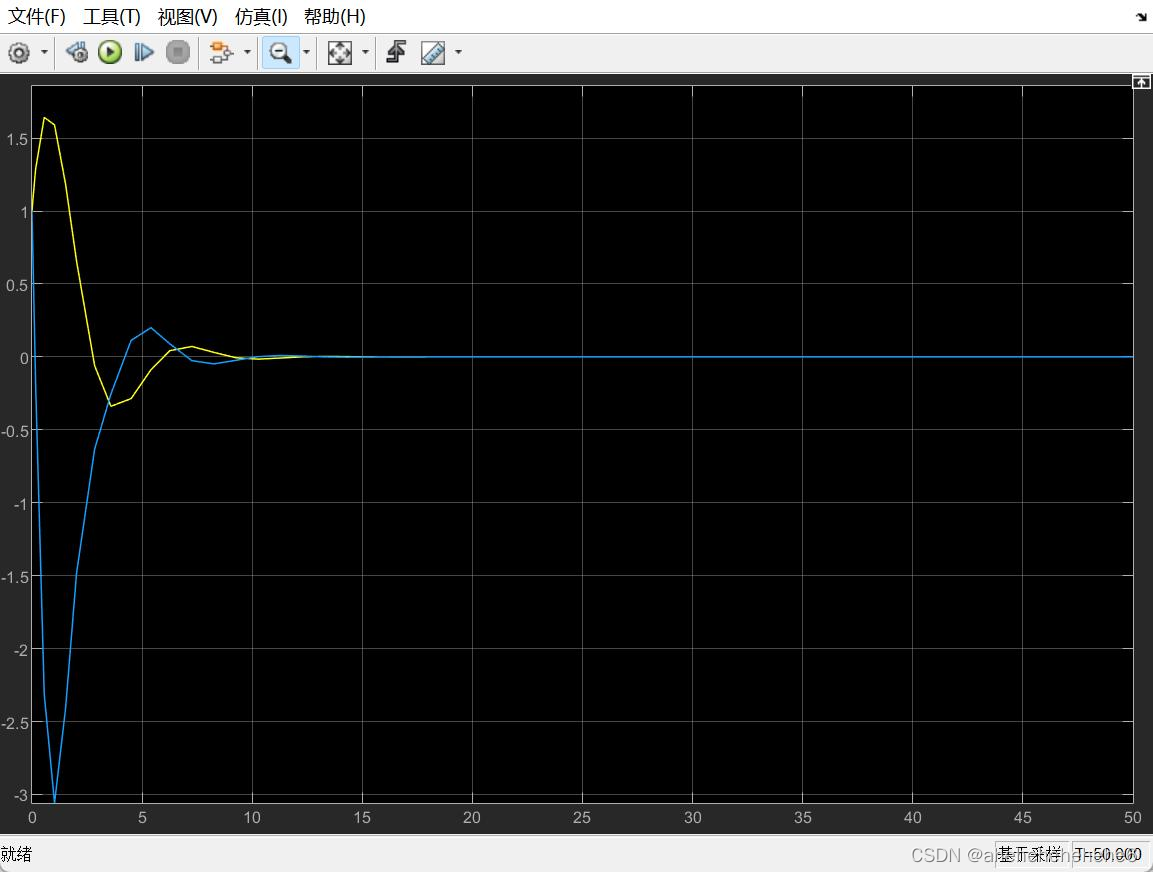
二、三自由度水下机器人航向控制
控制目标:
使水下机器人的航向角稳定在期望航向
寻找反馈控制律以及李雅普诺夫函数
使得原点
为全局渐进稳定的平衡点。
(1) 定义第一阶子系统的李雅普诺夫函数, 求导:
(2) 设计期望的状态变量形式, 令其为虚拟控制, 定义误差:
带入(1), 得到第一阶子系统状态的稳定项:
(3)
定义第二阶子系统的李雅普诺夫函数并求导:
(4)
设计控制器
,
使整个系统的  :
:
Simulink模块搭建:
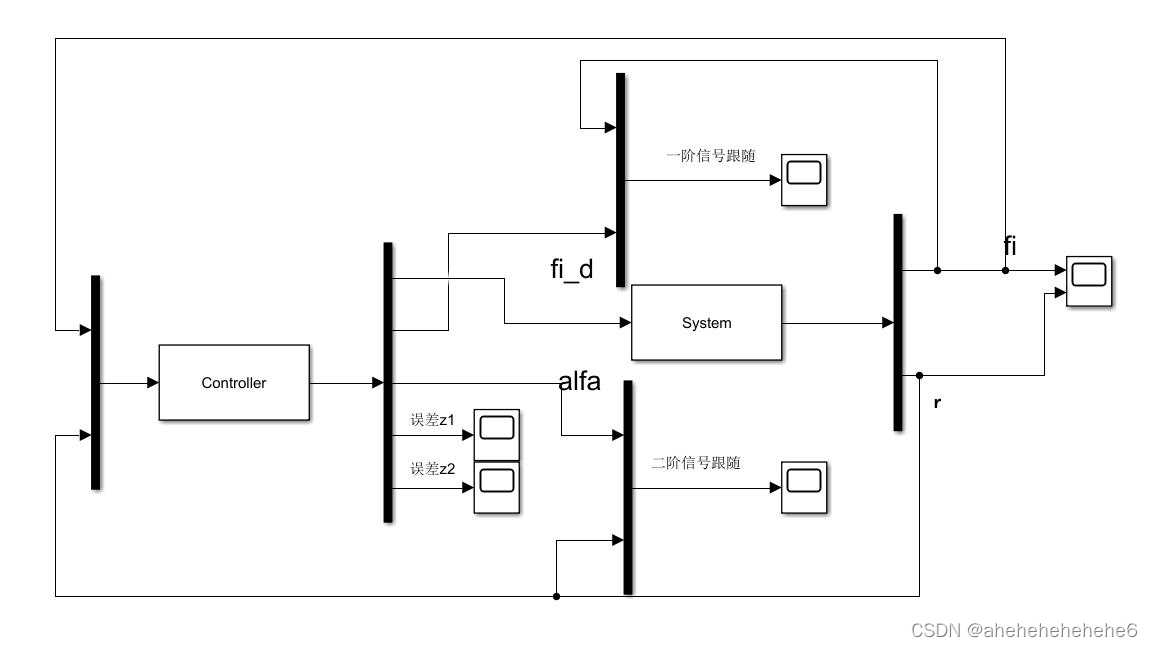
结果分析:
航向角跟随效果:
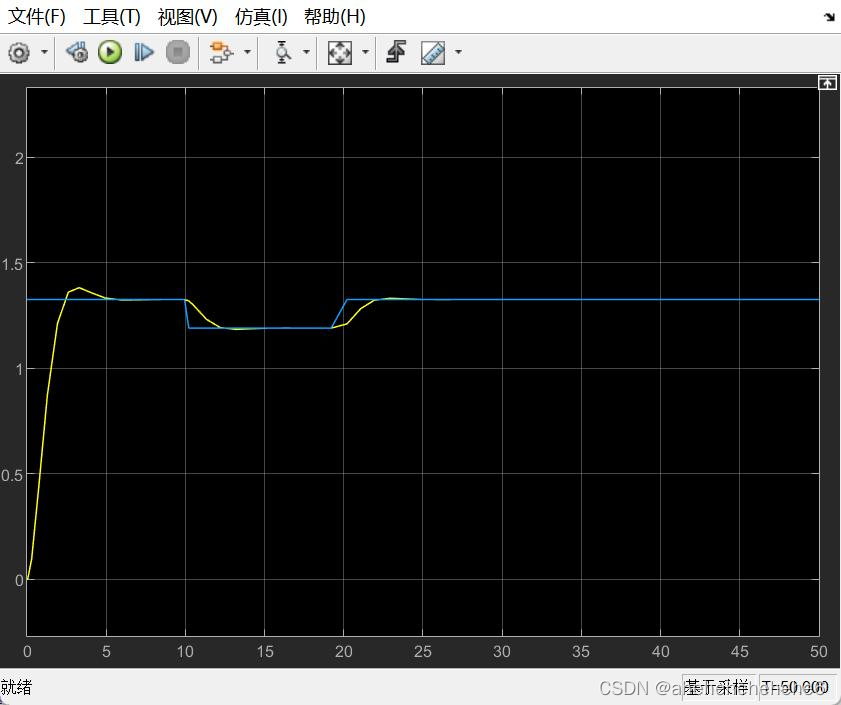
三、三自由度水下机器人平面路径跟踪控制
控制目标:
设计控制器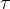 ,
使被控对象实际路径
,
使被控对象实际路径 跟踪期望的路径
跟踪期望的路径![\eta_d=$ $\left[x_d(\theta), y_d(\theta), \psi_d(\theta)\right]^T](https://latex.csdn.net/eq?%5Ceta_d%3D%24%20%24%5Cleft%5Bx_d%28%5Ctheta%29%2C%20y_d%28%5Ctheta%29%2C%20%5Cpsi_d%28%5Ctheta%29%5Cright%5D%5ET) ,
期望路径
,
期望路径 是关于
是关于 的函数
,
的函数
, 为虚拟动点的速度。水下机器人/无人船跟踪路径并趋近于该虚拟动点。
为虚拟动点的速度。水下机器人/无人船跟踪路径并趋近于该虚拟动点。
(1)
定义第一阶子系统的李雅普诺夫函数
,
求导:
(2) 设计期望的状态变量形式
,
令其为虚拟控制
,
定义期望的状态变量与虚拟控制之间
的误差:
带入
(1),
得到第一阶子系统状态的稳定项:
(3)
定义第二阶子系统的李雅普诺夫函数
并求导:
设计控制器:
(4) 无控制输入项
,
则可令下一级子系统的状态为虚拟控制
,
消除多余项如 ,相当于独立于系统之外的控制输入 (
虚拟动点
):
,相当于独立于系统之外的控制输入 (
虚拟动点
):
设计
 :
:
Simulink模块搭建:

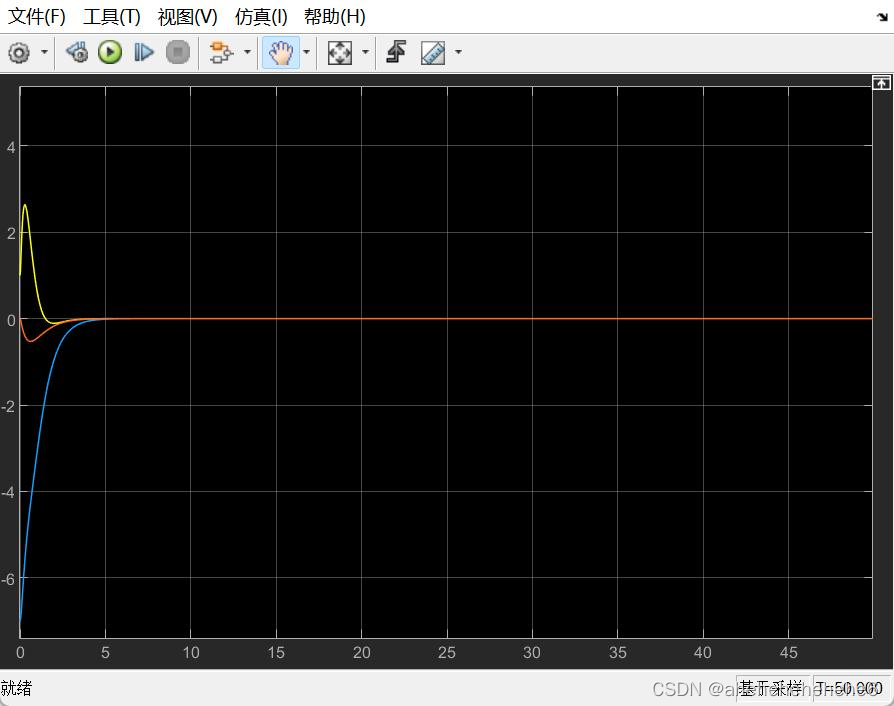
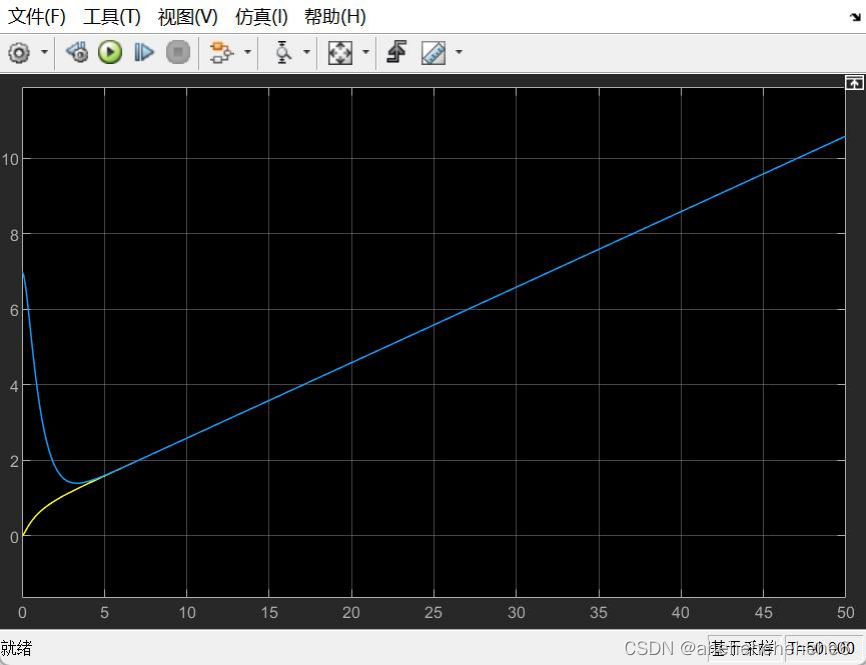
结果分析:
系统一阶误差
z1
收敛:
























 3005
3005











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








