最速下降法steepest descent详细解释

----------------------先闲聊几句------------------------------------
[1]首次提出了梯度下降法和最速下降法，既然柯西写出来了，所以这两个算法肯定不个一个东西,它们的区别是学习率是否恒定。
[4]提出了GoldStein法则

Wolfe准则以及Goldstein
[5][8]给出了具体的代码实现,
[6][7]中给出了手算steepest descent的例子

梯度的定义:
$gradf(x,y,z)=\frac{\partial f}{\partial x}\vec{i}+\frac{\partial f}{\partial y}\vec{j}$

然后稍微整理下目前学过的凸优化的一些方法:
1.steepest descent(默认无约束凸优化,使用欧式范数就是梯度下降,使用Hessian范数就是牛顿法,参考[10])
2.牛顿法(二阶牛顿法求最小值,多维即可涉及Hessian矩阵,计算量巨大,备受吐槽)
3.拟牛顿法(DFP、BFGS、L-BFGS)
4.共轭梯度法

而且Armijo-Goldstein法则和Wolfe-power法则的应用則是包含在上述算法的line-search環節中的
这篇博文是对[2]里面的内容进行进一步详细的阐述

--------------------闲谈结束,下面开始伪代码--------------------------
文的重点是描述steepest descent的原理细节.

首先是steepest descent算法伪代码[6]:
1.取初始点$X^{(0)}$,容许误差(精度)$ϵ>0,k:=0$
这里的:=符号的意思是"定义为"的意思.
2.计算$p^{(k)}=-▽f(X^{(k)})$
3.检验||$p^{(k)}$||≤$ϵ$?若是迭代终止,取$X^{\ast }=X^{(k)},$否则转4
4.求最有步长${\lambda }_k$,
$mi{n}_{\lambda \ge 0}f(X^{(k)}+{\lambda }_k{p}^k)=f(X^{(k)}+{\lambda }_k{p}^{(k)})$(一维搜索)
5.令$X^{(k+1)}=X^{(k)}+{\lambda }_k{p}^{(k)},令k:=k+1,转2$
注意:
2中利用了一个结论:一维搜索最优解的梯度$▽f(X^{(k+1)})与搜索方向p^{(k)}正交①$
[10]中虽然有理论证明,这里我来一个几何上面的直观解释吧:
为什么是正交的呢?

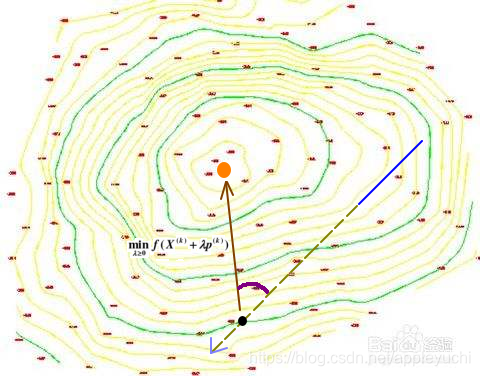
下面的黑线部分是$X^{(k)}$,
虚线部分是${\lambda }_k{p}^{(k)}$,
棕色线条的长度是${\lambda }_k,mi{n}_{\lambda \ge 0}f(X^{(k)}+{\lambda }_k{p}^{(k)})$
橙色的点是$f(X)=0$的坐标.

①中的结论等效于:
夹角多大的时候,${\lambda }_k,mi{n}_{\lambda \ge 0}f(X^{(k)}+{\lambda }_k{p}^{(k)})$得到最小值?
讲人话就是,角度多大,橙色点到虚线距离最短?
显然你们都知道:
点(橙色点)到直线距离是垂直的时候,距离最短,
从而①结论得证.

#--------------------------------根据上面的正交结论来证明${\lambda }_k$的取值,证明过程来自[6]---------------------------------------------
证明以下结论:
${\lambda }_k=\frac{g^{(k)T}{p}^{(k)}}{p^{(k)T}Q{p}^{(k)}}$

$f(X)=\frac{1}{2}{X}^{T}QX+b^{T}X+c$
准备工作:
令$g^{(k)}$$=▽f(X^{(k)})$
$▽f(X)=QX+b$
$X^{(k+1)}=X^{(k)}+{\lambda }_k{p}^{(k)}$
$▽f(X^{(k+1)}{)}^T{p}^{(k)}=0$
开始证明:
$g^{(k)}$
$=▽f(X^{(k)})$
$=Q{X}^{(k)}+b$

$g^{(k+1)}$
$=▽f(X^{(k+1)})$
$=Q{X}^{(k+1)}+b$
$=Q(X^{(k)}+{\lambda }_k{p}^k)+b$
$=Q{X}^{(k)}+b+{\lambda }_{k}Q{p}^{(k)}$
$=[Q{X}^{(k)}+b]+{\lambda }_{k}Q{p}^{(k)}$
$=g^{(k)}+{\lambda }_{k}Q{p}^{(k)}$

利用前面的结论:
$g^{(k+1)T}{p}^{(k)}$
$=(g^{(k)}+{\lambda }_{k}Q{p}^{(k)}{)}^T{p}^{(k)}$
$=g^{(k)T}{p}^{(k)}+{\lambda }_k{p}^{(k)T}Q{p}^{(k)}$
$=0$

得到:
${\lambda }_k=-\frac{g^{(k)T}{p}^{(k)}}{p^{(k)T}Q{p}^{(k)}}$

------------------------下面是手算steepest descent案例,来自[6]------------------------------------
用最速下降法求$f(X)=x_1^2+4x_2^2$的极小值点,
迭代两次.$X^{(0)}=(1,1{)}^T,ϵ=10^{-4}$

当然了,因为整个式子就是两个平方项,我们可以一眼看出,最终结果$X^{\ast }=(0,0{)}^T$
这里只是为了展示算法流程
求解:
$$f(X)=\frac{1}{2}(2x_1^2+8x_2^2)=\frac{1}{2}{X}^{T}QX$$

得到Q=$\left[\begin{array}{cc}2& 0\\ 0& 8\end{array}\right]$
$g(X)=▽f(X)=\left[\begin{array}{c}2x_1\\ 8x_2\end{array}\right]$
第一次迭代
1.k=0
2.$p^{(0)}=-g^{(0)}=-\left[\begin{array}{c}2\\ 8\end{array}\right]$

这里稍微说一下,这里为什盯着$p^{(0)}$的长度作为迭代终止条件呢?
这个要根据算法第4步骤来理解,
因为如果收敛,也就是到等高线额谷底的话,${\lambda }_k{p}^{(k)}$的数值肯定是很小的.
判断${\lambda }_k{p}^{(k)}$与判断$p^{(k)}$的迭代终止效果应该是一致的.
$||p^{(0)}||=\sqrt{(-2{)}^2+(-8{)}^2}=\sqrt{68}$

4.${\lambda }_0=-\frac{g^{(0)T}{p}^{(0)}}{p^{(0)T}Q{p}^{(0)}}=\frac{(2,8)\left[\begin{array}{c}2\\ 8\end{array}\right]}{(2,8)\left[\begin{array}{c}2,0\\ 0,8\end{array}\right]\left[\begin{array}{c}2\\ 8\end{array}\right]}=\frac{68}{520}=0.13077$
5.$X^{(1)}=X^{(0)}+{\lambda }_0{p}^{(0)}=\left[\begin{array}{c}1\\ 1\end{array}\right]-0.13077\left[\begin{array}{c}2\\ 8\end{array}\right]=\left[\begin{array}{c}0.73846\\ -0.04616\end{array}\right]$

第二次迭代
1.k=1
2.$p^{(1)}=-g^{(1)}=-\left[\begin{array}{c}1.47692\\ -0.39623\end{array}\right]$
3.||$p^{(1)}$||=1.52237
4.${\lambda }_1=-\frac{g^{(1)}T{p}^{(1)}}{p^{(1)T}Q{p}^{(1)}}=0.425$
5.$X^{(2)}=X^{(1)}+{\lambda }_1{p}^{(1)}=\left[\begin{array}{c}0.73846\\ -0.04616\end{array}\right]-0.425\left[\begin{array}{c}1.47692\\ -0.39623\end{array}\right]=\left[\begin{array}{c}0.11076\\ 0.11076\end{array}\right]$
k=2

然后再继续往下面迭代(略)
-----------------------------------------------------------------
steep descent具体代码实现是[5][8],但是注意,因为上面的手算没有使用Armijo-Goldstein法则和Wolfe-power法则,
但是[5][8]使用了Armijo-Goldstein法则,所以代码的运行过程和手算过程是对应不上的.
但是代码的运行结果是可以和手算结果对应上的
-----------------------------------------------------------------
Reference:
[1]Methode g ´ en´ erale pour la r ´ esolution des syst ´ emes `d’equations simultan ´ ees
[2]再谈 梯度下降法/最速下降法/Gradient descent/Steepest Descent
[3]文献已经没啥用了-已经删除.
[4]Cauchy’s method of minimization
[5]用Python实现最速下降法求极值
[6]最速下降法-百度文库
[7]【最优化】一文搞懂最速下降法
[8]最速下降法（梯度下降法）python实现
[9]Step-size Estimation for Unconstrained Optimization Methods
[10]梯度下降法和最速下降法的细微差别