目录
注释:是学习之余整理的资料,如有不对的地方还请指教,十分感谢!
1.单目标PSO的流程

适应度:个体的适应度(fitness)指的是个体在种群生存的优势程度度量,用于区分个体的“好与坏”。适应度使用适应度函数(fitness function)来进行计算。适应度函数也叫评价函数,主要是通过个体特征从而判断个体的适应度。
Pbest:粒子本身经历过的最优位置
Gbest:是粒子群经历过的最优位置
其中:
1、初始化粒子群位置是随机产生的;
2、速度更新公式 :![]()
PSO:是一种模拟社会行为、基于群体智能的进化技术。
MOPSO:将原来只能用在单目标上的粒子群算法应用于多目标。
问题一:如何选择MOPSO的pbest?
问题二:如何选择MOPSO的gbest?

问题一:
对于问题一的做法是在不能严格对比出哪个好一些时随机选择其中一个作为历史最优。
问题二:
对于问题二,MOPSO则在最优集里根据拥挤程度选择一个领导者(自适应网格法),尽量选择不那么密集位置的粒子(均匀分布)。
多目标粒子群算法MOPSO形象理解:
粒子看作50个人,可能潜在的700个解看做700个房间,还没被人打开。
初始:50个人每人随机进一个屋子,这个屋子的各项指标(温度,湿度等)叫做目标函数,这50个人心中都有一个脑子pbest,自己知道哪个屋子最好。
第一次按算法更新:50个人进入下一个房子。 下一个房子就是新解,有新的目标函数,如果这个屋子在各项指标都比上一个屋子好,那么pbest就是这个新解了,如果都没上一个好,pbest还是上一个pbest,如果互相不支配,那么随机从新解和pbest里选一个作为下次寻找房子的pbest。 Gbest相当于这50个人有个对讲机,他们每次寻找房子后都互相通气儿,有个全局意义上的最好的房子,为了能把这700个房子都找完,他们要做的就是为gbest设定为不密集的区域的房子(当然这个房子是非劣的房子)。
外部档案集相当于一个外界的笔记本,每次寻找后这50个人告诉了笔记本他们这次找到的10个非劣解房子,和笔记本里记录的30个房子比较下,40个房子里有两个房子被其他房子的目标支配,那么把他们删掉,剩下38个房子。但是笔记本只有30个空间,那么依据拥挤距离删掉8个,剩下30个。 那么这样寻找了100回合,最后在外部档案集里就是一个均匀的30个非劣解房子集合,这时候从这30个房子里去多目标决策挑选。
2.多目标PSO算法步骤

2.1初始阶段
给参数赋初值,初始化粒子的位置、速度,生成初始群体P1,评价粒子(适应值和pareto支配关系)并把P1中的非劣解拷贝到Archive集中得到A1。
 2.2进化产生下一代种群
2.2进化产生下一代种群
1)计算Archive 集中粒子的密度信息
把目标空间用网格等分成小区域,以每个区域中包含的粒子数作为粒子的密度信息。粒子所在网格中包含的粒子数越多,其密度值越大,反之越小。以二维目标空间最小化优化问题为例,密度信息估计算法的具体实现过程如下:


2)为群体中的粒子Pj,t 在At 中选择其gBest 粒子gj,t;gj,t 粒子的质量决定了MOPSO 算法的收敛性能和非劣解集的多样性,其选择依据是Archive 集中粒子的密度信息。
具体地,对于Archive 中的粒子,其密度值越低,选择的概率就越大,反之越小;用Archive 集中的粒子优于群体中的粒子数来评价其搜索潜力,优于群体中的粒子数越多,其搜索潜力越强,反之越弱。
算法的具体实现如下:

其中,|At|表示At 包含的粒子数;
Aj 用来存放At 中优于粒子Pj,t 的成员;
Aj 中密度最小的粒子存放在Gj 中;
Density(Ak)计算粒子Ak 的密度估计值;
Rand{Gj,t}表示从Gj,t 中随机选择一个成员。
3)更新群体中粒子的位置和速度群体中的粒子在gBest 和pBest 的引导下搜索最优解,算法的具体实现如下:

2.3更新Archive集
进化得到新一代群体Pt+1后,把Pt+1中的非劣解保存到Archive集中。算法的具体实现如下:

2.4Archive 集的截断操作
当 Archive 集中的粒子数超过了规定大小时,需要删除多余的个体以维持稳定的Archive 集规模。
对于粒子数多于1个的网格k,按下式计算该网格中要删除的粒子数PN,然后在网格k 中,随机删除PN 个粒子。

其中:
Grid[k]:表示网格k中的包含粒子数
3.对于PSO,MOPSO做出的改进
1、速度更新公式的优化,引入了一个收缩因子;
2、位置更新和越界处理;
3、增加了扰乱因子解决了算法快速收敛陷入局部最优的问题;
4、应用了自适应网格算法,改善了算法收敛性和多样性;
5、MOPSO的存档方法存档;
在种群更新完成之后,是如何进行存档的呢?
MOPSO进行了三轮筛选。
1、首先,根据支配关系进行第一轮筛选,将劣解去除,剩下的加入到存档中。
2、其次,在存档中根据支配关系进行第二轮筛选,将劣解去除,并计算存档粒子在网格中的位置。
3、最后,若存档数量超过了存档阀值,则根据自适应网格进行筛选,直到阀值限额为止。重新进行网格划分。
4.MOPSO的发展现状和应用

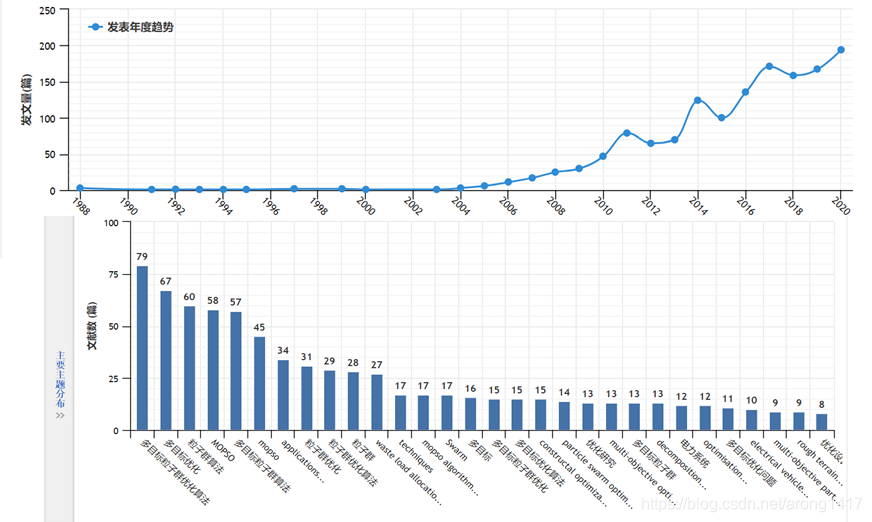








 本文介绍了多目标粒子群优化算法(MOPSO)的基本概念、流程及改进措施。包括单目标PSO流程、MOPSO算法步骤、改进方法及其发展现状和应用。详细解释了如何选择pbest和gbest,以及MOPSO的存档方法。
本文介绍了多目标粒子群优化算法(MOPSO)的基本概念、流程及改进措施。包括单目标PSO流程、MOPSO算法步骤、改进方法及其发展现状和应用。详细解释了如何选择pbest和gbest,以及MOPSO的存档方法。
















 539
539

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








