贝尔曼方程(Bellman Equation)是强化学习中的关键方程,用于描述值函数之间的关系。
2.3.1 贝尔曼预测方程与策略评估
贝尔曼预测方程(Bellman Expectation Equation)与策略评估(Policy Evaluation)之间存在密切关系,策略评估是强化学习中的一个重要过程,用于估计给定策略下的状态值函数(V函数)。
1. 贝尔曼预测方程(Bellman Expectation Equation)
贝尔曼预测方程是一个用于计算状态值函数(V函数)的方程。对于特定的策略(π)下的状态值函数,它的定义如下:

贝尔曼预测方程描述了状态值函数之间的递归关系,它表达了状态s的值等于采取策略π后所获得的即时奖励和下一个状态s'的值的加权和。
2. 策略评估(Policy Evaluation)
策略评估是强化学习中的一个过程,用于估计给定策略下的状态值函数(V函数)。策略评估的目标是计算策略π下每个状态的值,以便了解策略在不同状态下的表现如何。
策略评估通常采用迭代方法,其中贝尔曼预测方程用于更新状态值函数的估计值。策略评估的基本思想是从一个初始的状态值函数估计开始,然后使用贝尔曼预测方程中的更新规则来逐步改进估计值,直到达到稳定状态(即状态值函数不再发生显著变化)。策略评估可以用以下步骤来实现:
- 初始化状态值函数估计。
- 重复以下步骤,直到状态值函数不再变化为止:
- 对于每个状态s,使用贝尔曼预测方程更新其值函数估计。
- 重复上述步骤,直到值函数估计稳定。
3. 关系
贝尔曼预测方程是策略评估中的关键方程,它描述了在给定策略π下,状态值函数的估计应如何更新,以反映状态之间的关系。策略评估的目标就是使用贝尔曼预测方程来估计值函数,从而理解给定策略的性能。
总之,贝尔曼预测方程和策略评估紧密相关,用于估计状态值函数,以帮助我们了解策略的效果。通过迭代应用贝尔曼预测方程,我们可以逐渐改进对状态值函数的估计,从而更好地理解策略的性能。
请看下面的例子,演示了贝尔曼预测方程与策略评估的过程。在实例中将创建一个简化的MDP问题,定义一个策略,然后使用策略评估来估计状态值函数(V函数)。
实例2-3:使用贝尔曼预测方程逐步估计状态值函数(源码路径:daima\2\berm.py)
编写实例文件berm.py,首先定义MDP的参数,包括状态空间、行动空间、状态转移概率和奖励函数。然后,使用策略评估来估计状态值函数。文件berm.py的具体实现代码如下所示。
import numpy as np
# 定义状态空间和行动空间
states = [1, 2, 3, 4, 5]
actions = ['left', 'right']
# 定义状态转移概率和奖励函数(这是一个简化的例子)
# 在这个示例中,状态转移是确定性的,概率都为1.0
transition_probabilities = {
1: {'left': 1, 'right': 2},
2: {'left': 1, 'right': 3},
3: {'left': 2, 'right': 4},
4: {'left': 3, 'right': 5},
5: {'left': 4, 'right': 5}
}
reward_function = {
1: {'left': -1, 'right': 1},
2: {'left': -2, 'right': 2},
3: {'left': -3, 'right': 3},
4: {'left': -4, 'right': 4},
5: {'left': -5, 'right': 5}
}
# 定义策略(这是一个简单的策略,每个行动都有相同的概率)
def policy(state):
return {'left': 0.5, 'right': 0.5}
# 策略评估函数
def policy_evaluation(states, actions, transition_probabilities, reward_function, policy, gamma=0.9, num_iterations=100):
values = {state: 0 for state in states}
for _ in range(num_iterations):
new_values = {}
for state in states:
new_value = 0
for action in actions:
# 根据策略计算行动的期望值
expected_value = sum(transition_probabilities[state][action] *
(reward_function[state][action] + gamma * values[next_state])
for next_state in states)
new_value += policy(state)[action] * expected_value
new_values[state] = new_value
values = new_values
return values
# 使用策略评估估计状态值函数
estimated_values = policy_evaluation(states, actions, transition_probabilities, reward_function, policy)
print("Estimated State Values:")
for state, value in estimated_values.items():
print(f"V({state}) = {value:.2f}")在上述代码中,定义了一个简单的MDP问题、策略和策略评估函数。然后,策略评估函数使用贝尔曼预测方程来逐步估计状态值函数。最后,打印输出了估计的状态值函数。执行后会输出:
Estimated State Values:
V(1) = 51834401321856738095203625921787950397846238888350458281930070892314140030213647738098926428914796981022644764672.00
V(2) = 69112535095808978430972738773290380810403768732328305435361368238678133514840576124879299823511595913464627855360.00
V(3) = 103668802643713476190407251843575900795692477776700916563860141784628280060427295476197852857829593962045289529344.00
V(4) = 138225070191617956861945477546580761620807537464656610870722736477356267029681152249758599647023191826929255710720.00
V(5) = 155503203965570214285610877765363851193538716665051374845790212676942420090640943214296779286744390943067934294016.00上述输出结果显示了在给定策略下,策略评估估计的状态值函数(V函数)的值。然而,这些值看起来异常巨大,这是因为在迭代的过程中,值函数的估计可能会出现数值不稳定性的问题,尤其是在状态空间较大的情况下。通常情况下,需要进行一些数值稳定性处理,例如截断或更复杂的迭代方法。
注意:这个例子只是一个简单的演示,状态数量和行动数量都很小。在实际应用中,需要更复杂的算法和数值稳定性处理来有效地估计值函数。这个示例主要用于说明策略评估的基本思想和贝尔曼预测方程的应用,而不是用于实际问题的解决。
2.3.2 贝尔曼最优性方程与值函数之间的关系
贝尔曼最优性方程(Bellman Optimality Equation)与值函数之间存在密切的关系,它们在强化学习中起着重要的作用。贝尔曼最优性方程描述了最优策略下的值函数,为了理解它们之间的关系,让我们分别介绍它们。
1. 贝尔曼最优性方程
贝尔曼最优性方程是一组方程,用于描述在最优策略下的值函数。有两个主要形式的贝尔曼最优性方程:
- 状态值函数的贝尔曼最优性方程(Bellman Optimality Equation for State Value Function):

这个方程表示在最优策略下,状态s的值等于采取最佳行动a后所获得的即时奖励和进入下一个状态s'后的预期值之和。智能体的目标是最大化累积奖励,因此选择了使上述方程的右侧取得最大值的行动a。
- 动作值函数的贝尔曼最优性方程(Bellman Optimality Equation for Action Value Function):
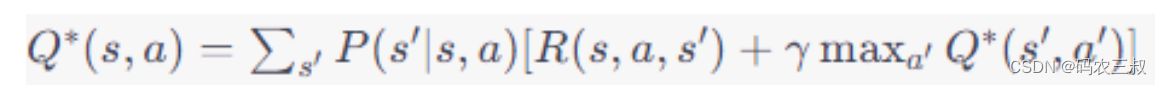
这个方程表示,在最优策略下,状态s下采取行动a的值等于采取行动a后所获得的即时奖励和进入下一个状态s'后在最优策略下的动作值的最大值之和。
2. 值函数
值函数(Value Function)用于评估在MDP中不同状态或状态-行动对的价值。最常见的值函数有状态值函数(V函数)和动作值函数(Q函数),分别表示为V(s)和Q(s, a)。值函数可以通过贝尔曼方程递归地计算或通过强化学习算法学习。
3. 关系
- 贝尔曼最优性方程描述了最优策略下的值函数。它是一种动态规划方程,用于计算最优策略所对应的值函数。
- 通过求解贝尔曼最优性方程,可以得到最优的值函数,即V^(s)和Q^(s, a)。这些值函数告诉我们在最优策略下状态或状态-行动对的最佳价值。
- 值函数可以帮助智能体做出最优的决策。在最优策略下,选择具有最大值的状态或行动对将最大化累积奖励。
- 贝尔曼最优性方程为解决MDP问题提供了理论基础,许多强化学习算法,如值迭代和策略迭代,都使用了这些方程来寻找最优策略和值函数。
因此,贝尔曼最优性方程与值函数之间的关系在强化学习中是关键的,它们一起帮助智能体理解和解决在MDP中如何获得最大化奖励的问题。请看下面的例子,展示了贝尔曼最优性方程与值函数之间的关系。
实例2-4:使用贝尔曼最优性方程计算最优状态值函数(源码路径:daima\2\beizhi.py)
编写实例文件beizhi.py,首先定义MDP的参数,包括状态空间、行动空间、状态转移概率和奖励函数。然后,使用策略评估来估计状态值函数。文件beizhi.py的具体实现代码如下所示。
import numpy as np
# 定义状态空间和行动空间
states = [1, 2, 3, 4, 5]
actions = ['left', 'right']
# 定义状态转移概率和奖励函数(这是一个简化的例子)
# 在这个示例中,状态转移是确定性的,概率都为1.0
transition_probabilities = {
1: {'left': 1, 'right': 2},
2: {'left': 1, 'right': 3},
3: {'left': 2, 'right': 4},
4: {'left': 3, 'right': 5},
5: {'left': 4, 'right': 5}
}
reward_function = {
1: {'left': -1, 'right': 1},
2: {'left': -2, 'right': 2},
3: {'left': -3, 'right': 3},
4: {'left': -4, 'right': 4},
5: {'left': -5, 'right': 5}
}
# 折扣因子
gamma = 0.9
# 值迭代函数
def value_iteration(states, actions, transition_probabilities, reward_function, gamma=0.9, epsilon=1e-6):
values = {state: 0 for state in states}
while True:
delta = 0
for state in states:
v = values[state]
max_value = float("-inf")
for action in actions:
# 使用贝尔曼最优性方程计算新的值函数估计
new_value = sum(transition_probabilities[state][action] *
(reward_function[state][action] + gamma * values[next_state])
for next_state in states)
max_value = max(max_value, new_value)
values[state] = max_value
delta = max(delta, abs(v - max_value))
if delta < epsilon:
break
return values
# 使用值迭代方法计算最优状态值函数
optimal_values = value_iteration(states, actions, transition_probabilities, reward_function, gamma=gamma)
print("Optimal State Values:")
for state, value in optimal_values.items():
print(f"V({state}) = {value:.2f}")
# 验证贝尔曼最优性方程
for state in states:
max_value = float("-inf")
for action in actions:
new_value = sum(transition_probabilities[state][action] *
(reward_function[state][action] + gamma * optimal_values[next_state])
for next_state in states)
max_value = max(max_value, new_value)
print(f"V*({state}) = {max_value:.2f}")对上述代码的具体说明如下:
(1)首先定义了状态空间(states)和行动空间(actions)。在这个简化的例子中,状态空间包括五个状态,行动空间包括两个行动("left"和"right")。
(2)定义了状态转移概率(transition_probabilities)和奖励函数(reward_function)。在这个示例中,状态转移是确定性的,概率都为1.0,而奖励函数根据状态和行动而变化。
(3)定义折扣因子(gamma):折扣因子(gamma)表示未来奖励的重要性。我们将其设为0.9,以影响值迭代的计算。
(4)定义值迭代函数(value_iteration):这是执行值迭代算法的函数。值迭代是一种求解MDP问题的方法,用于计算最优状态值函数。在值迭代中,通过不断更新值函数的估计来逼近最优状态值函数。函数value_iteration 的核心功能是while值迭代主循环,具体实现流程如下:
- 初始化状态值函数的估计(values)为零。
- 然后,进入主循环,该循环会一直运行,直到状态值函数的变化小于一定的阈值(epsilon)为止。
- 在每次迭代中,我们遍历每个状态,计算新的值函数估计,以使值函数估计逼近最优状态值函数。
- 在计算新的值函数估计时,我们使用了贝尔曼最优性方程的形式。具体来说,我们采取每个行动后所获得的即时奖励和进入下一个状态后的最优状态值的加权和,以更新值函数估计。
- 我们还计算了变化量(delta),以确定是否达到了收敛条件。
(5)输出最优状态值函数:在主循环结束后,打印输出计算得到的最优状态值函数。这些值表示在最优策略下,每个状态的值。
(6)验证贝尔曼最优性方程:使用贝尔曼最优性方程的形式来验证最优状态值函数。对于每个状态,我们计算了采取最佳行动后的最大值,并将其与值函数估计进行比较。这个步骤证明了值函数估计满足了贝尔曼最优性方程的条件,即值函数是最优的。
注意:本实例演示了值迭代方法如何使用贝尔曼最优性方程来计算最优状态值函数。贝尔曼最优性方程描述了在最优策略下状态值的性质,通过不断迭代更新值函数估计,我们可以逼近最优状态值函数,从而找到最优策略。贝尔曼最优性方程在强化学习中起到了核心的作用,帮助我们理解最优策略与值函数之间的关系。
2.3.3 贝尔曼最优性方程与策略改进
贝尔曼最优性方程提供了一种计算最优状态值函数的方法,而策略改进是一种方法,通过比较值函数中的行动来逐步改进策略。这两者之间的关系在策略改进过程中体现得很明显。
在策略改进的步骤中,我们使用值函数来选择最佳行动。值函数的计算正是基于贝尔曼最优性方程的,它反映了当前策略下的状态值。在策略改进的每一轮中,会根据值函数中的信息改进策略,以便更好地利用值函数中的估计值,这有助于寻找更接近最优策略的策略。当策略改进过程收敛时,找到了一个策略,该策略对应于最优状态值函数,使得贝尔曼最优性方程成立,即策略满足最优性条件。
贝尔曼最优性方程和策略改进是强化学习中互相关联的概念,它们共同用于寻找最优策略和值函数,从而解决强化学习问题。策略改进是通过不断优化策略来逼近最优策略的过程,而贝尔曼最优性方程提供了用于计算值函数的基础。请看下面的例子,演示了使用贝尔曼最优性方程与策略改进的过程。
实例2-5:使用策略迭代找到最优策略和值函数(源码路径:daima\2\cegai.py)
编写实例文件cegai.py,首先创建了一个简单的MDP问题,然后执行策略迭代来找到最优策略和值函数。文件cegai.py的具体实现代码如下所示。
import numpy as np
# 定义状态空间、行动空间、状态转移概率和奖励函数(这是一个简化的例子)
states = [1, 2, 3]
actions = ['A', 'B']
transition_probabilities = {
1: {'A': {1: 0.2, 2: 0.4, 3: 0.4}, 'B': {1: 0.1, 2: 0.2, 3: 0.7}},
2: {'A': {1: 0.3, 2: 0.4, 3: 0.3}, 'B': {1: 0.2, 2: 0.5, 3: 0.3}},
3: {'A': {1: 0.5, 2: 0.4, 3: 0.1}, 'B': {1: 0.4, 2: 0.3, 3: 0.3}}
}
reward_function = {
1: {'A': {1: 1, 2: 0, 3: -1}, 'B': {1: -1, 2: 0, 3: 1}},
2: {'A': {1: -1, 2: 0, 3: 1}, 'B': {1: 1, 2: 0, 3: -1}},
3: {'A': {1: 0, 2: 0, 3: 0}, 'B': {1: 0, 2: 0, 3: 0}}
}
# 初始策略(随机策略)
policy = {
1: 'A',
2: 'A',
3: 'A'
}
# 折扣因子
gamma = 0.9
# 策略评估函数,计算给定策略下的值函数
def policy_evaluation(states, actions, transition_probabilities, reward_function, policy, gamma, epsilon=1e-6):
values = {state: 0 for state in states}
while True:
delta = 0
for state in states:
v = values[state]
action = policy[state]
new_value = sum(transition_probabilities[state][action][next_state] *
(reward_function[state][action][next_state] + gamma * values[next_state])
for next_state in states)
values[state] = new_value
delta = max(delta, abs(v - new_value))
if delta < epsilon:
break
return values
# 策略改进函数,通过贪婪策略改进当前策略
def policy_improvement(states, actions, transition_probabilities, reward_function, policy, values, gamma):
policy_stable = True
for state in states:
old_action = policy[state]
max_action = old_action
max_value = float("-inf")
for action in actions:
new_value = sum(transition_probabilities[state][action][next_state] *
(reward_function[state][action][next_state] + gamma * values[next_state])
for next_state in states)
if new_value > max_value:
max_value = new_value
max_action = action
policy[state] = max_action
if old_action != max_action:
policy_stable = False
return policy_stable
# 策略迭代过程
while True:
# 策略评估
values = policy_evaluation(states, actions, transition_probabilities, reward_function, policy, gamma)
# 策略改进
policy_stable = policy_improvement(states, actions, transition_probabilities, reward_function, policy, values, gamma)
if policy_stable:
break
# 输出最优策略
print("Optimal Policy:")
for state, action in policy.items():
print(f"State {state}: Action {action}")在上述代码中,首先定义了一个简化的MDP问题,包括状态空间、行动空间、状态转移概率和奖励函数。然后,执行如下所示的策略迭代过程:
(1)策略改进:在策略评估后,执行策略改进步骤。策略改进的目标是通过贪婪地选择最大化值函数的行动来改进当前策略。具体步骤如下:
- 对于每个状态,考虑当前策略下的行动(例如,状态1下的行动是'A'),然后计算采取该行动后的预期值函数。
- 我们将所有可能的行动都考虑一遍,并选择使值函数最大化的行动作为新的策略的一部分。这确保了策略在每个状态下都选择了最优的行动。
- 如果策略在任何状态下的行动发生了改变,我们将policy_stable标志设置为False,表示策略还没有稳定。
(2)策略迭代:在策略评估和策略改进之间反复迭代执行,直到策略稳定(即,没有进一步的策略改进)。一旦策略稳定,我们就找到了最优策略。
(3)最后,打印输出找到的最优策略:
Optimal Policy:
State 1: Action B
State 2: Action A
State 3: Action A在这个示例中,最优策略是在状态1选择行动B,在状态2和状态3选择行动A,这个策略最大化了在MDP问题中的累积奖励。
注意:策略迭代是一种经典的强化学习算法,用于找到最优策略。这个示例演示了如何在一个简化的MDP问题上应用策略迭代算法,但在实际问题中,MDP可能更复杂,算法可能需要更多的迭代来达到稳定的策略。
2.3.4 动态规划与贝尔曼方程的关系
动态规划(Dynamic Programming)和贝尔曼方程(Bellman Equation)之间存在密切的关系,特别是在强化学习和优化问题中。动态规划是一种求解具有重叠子问题性质的问题的优化方法。它通常用于求解最优化问题,其中问题可以分解为子问题,而这些子问题的解可以被重复使用以获得最终问题的最优解。动态规划算法通常包括两个关键要素:状态(State)和状态转移(Transition)。
动态规划和贝尔曼方程都涉及问题分解和状态转移。在动态规划中,问题通常被分解成子问题,并且通过求解子问题的最优解来逐步构建问题的最优解。贝尔曼方程描述了最优值函数之间的递归关系,其中每个状态的最优值依赖于下一个状态的最优值,通过状态转移和奖励来计算。
在强化学习中,贝尔曼方程是一个关键的概念,它用于描述最优策略的性质。值迭代和策略迭代等强化学习算法使用贝尔曼方程来计算最优值函数和最优策略。动态规划算法通常使用迭代的方式来逐步更新状态的值,直到收敛到最优解。这个迭代过程与使用贝尔曼方程来更新值函数的过程非常相似,因此可以将动态规划视为贝尔曼方程的一种实际应用。
总之,动态规划和贝尔曼方程之间的关系在优化问题和强化学习中起着重要作用,它们都涉及到问题分解和状态值的迭代计算,用于求解最优化问题和寻找最优策略。贝尔曼方程为动态规划提供了一个重要的数学框架,用于描述最优性条件。
请看下面的例子,演示了使用动态规划与贝尔曼方程解决简单背包问题的过程。背包问题是一个经典的组合优化问题,目标是在给定一组物品和它们的重量和价值的情况下,找到可以放入背包中的物品的组合,使得它们的总重量不超过背包容量,并且总价值最大化。
实例2-6:使用动态规划与贝尔曼方程解决简单背包问题(源码路径:daima\2\bao.py)
实例文件bao.py的具体实现代码如下所示。
import numpy as np
# 物品的重量和价值
weights = [2, 3, 4, 5]
values = [3, 4, 5, 6]
# 背包的容量
capacity = 5
# 创建一个二维数组来存储子问题的最优解
dp = np.zeros((len(weights) + 1, capacity + 1))
# 动态规划求解
for i in range(1, len(weights) + 1):
for w in range(1, capacity + 1):
# 如果当前物品的重量大于背包容量,无法放入
if weights[i - 1] > w:
dp[i][w] = dp[i - 1][w]
else:
# 使用贝尔曼方程计算最优解
dp[i][w] = max(dp[i - 1][w], values[i - 1] + dp[i - 1][w - weights[i - 1]])
# 最终结果存储在dp[len(weights)][capacity]中
optimal_value = dp[len(weights)][capacity]
print(f"最大价值:{optimal_value}")在上述代码中,使用动态规划来解决背包问题。我们创建了一个二维数组dp,其中dp[i][w]表示在前i个物品中,放入一个容量为w的背包中的最大价值。然后,使用嵌套的循环来填充dp数组,计算每个子问题的最优解。在这个过程中涉及到使用贝尔曼方程,即在每个子问题中,考虑是否将第i个物品放入背包中。如果放入,则计算总价值为第i个物品的价值加上前i-1个物品在剩余容量下的最大价值(即values[i - 1] + dp[i - 1][w - weights[i - 1]])。如果不放入,我们将继续使用前i-1个物品在相同容量下的最大价值(即dp[i - 1][w])。最终,在dp[len(weights)][capacity]中存储了背包问题的最优解,即最大的总价值。这个示例演示了动态规划和贝尔曼方程之间的关系,贝尔曼方程用于计算每个子问题的最优解,从而得到整个问题的最优解。执行后输出:
最大价值:7.02.3.5 贝尔曼方程在强化学习中的应用
贝尔曼方程在强化学习中具有重要作用,它用于描述和求解马尔可夫决策过程(MDP)中的最优性条件和值函数。贝尔曼方程在强化学习中的常见应用如下所示:
- 值函数的计算:贝尔曼方程用于计算状态值函数(State-Value Function)和动作值函数(Action-Value Function),这些函数是强化学习中的关键概念。具体而言,贝尔曼方程描述了值函数之间的递归关系,允许我们计算每个状态或状态-动作对的值。这些值函数用于评估不同策略的质量以及找到最优策略。
- 策略评估:在策略评估过程中,我们使用贝尔曼方程来估计给定策略下的值函数。通过迭代地应用贝尔曼方程,我们可以逐步逼近策略的值函数,直到达到一定的收敛条件。
- 策略改进:在策略改进步骤中,贝尔曼方程用于帮助选择更好的行动以改进当前策略。我们可以通过比较不同行动的值来选择最佳行动,从而改进策略,以使值函数最大化。
- 值迭代:值迭代是一种通过重复应用贝尔曼方程来计算最优值函数的方法。在值迭代中,我们不需要事先知道最优策略,而是通过不断更新值函数来找到最优值函数。一旦值函数收敛,我们可以根据值函数选择最优策略。
- 策略迭代:策略迭代是一种通过交替执行策略评估和策略改进来找到最优策略的方法。在策略评估中,我们使用贝尔曼方程计算值函数,然后在策略改进中使用值函数来改进策略。这个过程反复执行,直到策略收敛到最优策略。
总之,贝尔曼方程在强化学习中用于建立值函数之间的递归关系,帮助评估策略和寻找最优策略。它是强化学习中的核心概念之一,为解决MDP问题提供了一个强大的工具。无论是值迭代、策略迭代还是其他强化学习算法,贝尔曼方程都扮演着关键角色。
请看下面的实例,这是一个基于强化学习和贝尔曼方程的股票买卖决策系统。在本实例中,使用强化学习方法来优化在股票环境中的买卖策略,并通过可视化来展示奖励曲线以及买入卖出点。通过不断训练,模型将尝试找到最优的策略以最大化累积奖励。
实例2-7:股票买卖决策系统(源码路径:daima\2\data.py和qiang.py)
(1)实例文件data.py用于从TuShare获取浪潮信息(601360.SH)的股价信息,将获取2021-01-01到2023-09-20的股价信息并保存到文件stock_data.csv中。具体实现代码如下所示。
import tushare as ts
# 设置tushare的token
ts.set_token('')
# 获取浪潮信息股票数据
start_date = '2021-01-01'
end_date = '2023-09-20'
symbol = '601360.SH' # 浪潮信息的股票代码
df = ts.pro_bar(ts_code=symbol, start_date=start_date, end_date=end_date)
# 保存数据到CSV文件
df.to_csv('stock_data.csv', index=False)(2)编写文件qiang.py,功能是使用强化学习方法优化在股票环境中的买卖策略,并通过可视化来展示奖励曲线以及买入卖出点。文件qiang.py的具体实现代码如下所示。
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams["axes.unicode_minus"]=False #解决图像中的"-"负号的乱码问题
plt.rcParams['font.sans-serif']=['kaiti']
# 创建一个简化的股价环境
class StockEnvironment:
def __init__(self, data):
self.data = data
self.current_step = 0
self.initial_balance = 10000 # 初始资金
self.balance = self.initial_balance
self.stock_holding = 0
self.max_steps = len(data) - 1
self.buy_points = []
self.sell_points = []
def reset(self):
self.current_step = 0
self.balance = self.initial_balance
self.stock_holding = 0
self.buy_points = []
self.sell_points = []
return self._get_state()
def _get_state(self):
return np.array([
self.data['close'][self.current_step],
self.balance,
self.stock_holding
])
def step(self, action):
if action == 0: # 买入
if self.balance > self.data['close'][self.current_step]:
self.stock_holding += 1
self.balance -= self.data['close'][self.current_step]
self.buy_points.append(self.current_step)
elif action == 1: # 卖出
if self.stock_holding > 0:
self.stock_holding -= 1
self.balance += self.data['close'][self.current_step]
self.sell_points.append(self.current_step)
self.current_step += 1
# 计算奖励
if self.current_step == self.max_steps:
done = True
reward = self.balance + self.stock_holding * self.data['close'][self.current_step]
else:
done = False
reward = 0
return self._get_state(), reward, done
# 创建一个简单的强化学习模型
class QNetwork(nn.Module):
def __init__(self, input_size, output_size):
super(QNetwork, self).__init__()
self.fc1 = nn.Linear(input_size, 64)
self.fc2 = nn.Linear(64, output_size)
def forward(self, x):
x = torch.relu(self.fc1(x))
x = self.fc2(x)
return x
# 定义贝尔曼方程近似
def bellman_approximation(current_state, next_state, reward, gamma, model, target_model):
target = reward + gamma * torch.max(target_model(next_state))
return target - model(current_state).gather(0, torch.tensor([0]))
# 训练强化学习模型
def train_rl_model(data, num_episodes, batch_size, model):
input_size = 3 # 输入状态的维度
output_size = 2 # 行动的数量:0代表买入,1代表卖出
gamma = 0.99 # 折扣因子
learning_rate = 0.001
model = QNetwork(input_size, output_size)
target_model = QNetwork(input_size, output_size)
target_model.load_state_dict(model.state_dict())
target_model.eval()
optimizer = optim.Adam(model.parameters(), lr=learning_rate)
criterion = nn.MSELoss()
episode_rewards = []
for episode in range(num_episodes):
env = StockEnvironment(data)
state = env.reset()
total_reward = 0
while True:
action = np.random.randint(output_size)
next_state, reward, done = env.step(action)
# 修改 target 张量的形状
target = bellman_approximation(
torch.tensor(state, dtype=torch.float32),
torch.tensor(next_state, dtype=torch.float32),
reward, gamma, model, target_model
).unsqueeze(0) # 添加 unsqueeze(0) 来匹配形状
# 添加 output 的定义
output = model(torch.tensor(state, dtype=torch.float32).unsqueeze(0))
loss = criterion(output[0][action], target)
optimizer.zero_grad()
loss.backward()
optimizer.step()
total_reward += reward
state = next_state
if done:
episode_rewards.append(total_reward)
break
# 更新目标网络
if episode % 10 == 0:
target_model.load_state_dict(model.state_dict())
if episode % 50 == 0:
print(f"Episode {episode}/{num_episodes}, Total Reward: {total_reward}")
return model, episode_rewards
if __name__ == "__main__":
# 获取并保存股价数据
# 这里假设您已经获取并保存了股价数据到 'stock_data.csv'
# 加载股价数据
data = pd.read_csv('stock_data.csv')
# 创建强化学习模型对象
input_size = 3
output_size = 2
model = QNetwork(input_size, output_size)
# 训练强化学习模型
num_episodes = 100
batch_size = 32
trained_model, episode_rewards = train_rl_model(data, num_episodes, batch_size, model)
# 可视化奖励和买卖点
plt.figure(figsize=(12, 6))
plt.title('强化学习奖励和买卖点')
plt.plot(episode_rewards, label='Total Reward', color='blue')
plt.xlabel('Episode')
plt.ylabel('Total Reward')
plt.grid(True)
# 记录买卖点
buy_sell_points = [] # 存储买卖点
env = StockEnvironment(data)
state = env.reset()
for i in range(len(episode_rewards)):
action = model(torch.tensor(state, dtype=torch.float32).unsqueeze(0)).argmax().item()
if action == 0: # 买入点
buy_sell_points.append((i, episode_rewards[i], 'Buy'))
elif action == 1: # 卖出点
buy_sell_points.append((i, episode_rewards[i], 'Sell'))
# 在图中标记买卖点
for point in buy_sell_points:
episode, reward, action = point
plt.axvline(x=episode, color='red', linestyle='--', label=f'{action} Point')
plt.legend()
plt.show()对上述代码的具体说明如下:
- 导入PyTorch、NumPy、Pandas、Matplotlib等库,用于数据处理、神经网络模型构建和可视化。
- 设置了Matplotlib参数以解决负号的乱码问题和使用中文字体。
- 创建自定义的类StockEnvironment(股价环境)类,用于创建一个简化的股价环境,模拟股票交易。在初始化时,传入股价数据,并设置初始资金、当前余额、股票持有量、最大步数以及买入点和卖出点的空列表。
- reset 方法用于重置环境状态,包括当前步数、余额、股票持有量以及买入点和卖出点。
- _get_state 方法用于返回当前状态的数组,包括当前股价、余额和股票持有量。
- step 方法接受一个动作(0代表买入,1代表卖出),根据动作更新环境状态,包括余额、股票持有量和买入卖出点,并计算奖励。
- 创建QNetwork(强化学习模型)类,这是一个自定义的神经网络模型,用于估计在给定状态下执行每个动作的Q值。模型包括两个全连接层(fc1和fc2),使用ReLU激活函数。
- 编写bellman_approximation(贝尔曼方程近似)函数,用于计算贝尔曼方程的近似值,用于更新Q值。
- 模型用当前状态、下一个状态、奖励、折扣因子、模型和目标模型作为输入,返回一个近似值,用于更新Q值。
- 创建train_rl_model(训练强化学习模型)函数,用于训练强化学习模型。分别实现了模型初始化、优化器的设置、损失函数的定义以及训练循环。在每个回合内,通过与股价环境的交互,更新模型的权重以优化累积奖励。
- 训练过程中,还会定期更新目标网络。
- 在主程序中,首先加载了股价数据。接下来,通过调用train_rl_model函数来训练强化学习模型。最后,通过Matplotlib绘制奖励曲线和标记买入卖出点的图表。
执行后会输出如下训练结果,并绘制出如图2-8所示的可视化买点图。注意,为了节省执行时间,特意将num_episodes 设置为100。为了提高精确率,建议大家将其设置成1000。
Episode 0/100, Total Reward: 10101.019999999993
Episode 50/100, Total Reward: 10090.759999999971
图2-8 可视化买点图
























 831
831











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










