
PID 控制作为工业自动化的核心技术,其智能化演进始终围绕解决传统比例 - 积分 - 微分控制在复杂动态系统中的局限性展开。早期 PID 依赖人工经验整定参数,难以适应非线性、时变或强耦合系统,而智能化升级通过融合自适应算法、模糊逻辑、神经网络、强化学习等技术,实现了参数的自主优化 —— 例如,模糊 PID 可根据系统实时偏差动态调整比例系数、积分时间和微分时间,神经网络 PID 能通过数据学习逼近复杂系统模型,强化学习则能在未知环境中通过试错迭代找到最优控制策略。这种演进不仅让 PID 具备了处理多变量、强干扰场景的能力,还能结合工业互联网实现远程自适应调节,在智能制造、机器人控制、流程工业等领域显著提升了控制精度与系统鲁棒性,成为连接经典控制理论与智能自动化的重要桥梁。
5.1 新型PID架构
新型PID架构以智能算法为核心,通过模糊逻辑、神经网络动态适配参数,突破传统固定参数局限。新型PID架构融合了工业大数据与实时感知技术,实现工况突变时的自主调节与多变量协同控制。
5.1.1 模糊自适应PID
模糊自适应PID(F-PID)控制器是一种将模糊控制与传统PID控制相结合的智能控制器,旨在克服传统PID控制器在面对复杂、非线性、时变系统时参数难以实时调整的缺陷。
1. 基本原理
模糊自适应PID控制器的核心在于利用模糊逻辑对PID参数进行在线调整。其输入为系统的偏差(误差)e和偏差变化率(误差变化)ec,输出为PID控制器的比例系数Kp、积分系数Ki和微分系数Kd的调整量。通过模糊推理机制,根据输入的模糊化处理和预设的模糊规则,动态调整PID参数,以适应不同的系统状态,从而优化控制效果。
2. 结构组成
模糊自适应PID控制器通常由以下部分组成。
- 模糊化接口:将精确的输入变量(如误差和误差变化率)转换为模糊集合,以便进行模糊推理。
- 模糊规则库:存储基于专家经验和系统特性制定的模糊规则,这些规则定义了输入与输出之间的关系。
- 模糊推理引擎:根据模糊规则和输入的模糊集合进行推理,得出模糊输出。
- 去模糊化接口:将模糊推理得出的模糊输出转换为精确的控制参数(如Kp、Ki、Kd的调整量),用于调整PID控制器的参数。
- PID控制器:根据调整后的参数进行控制操作。
3. 优势
- 适应性强:能够根据系统的实时状态动态调整PID参数,适应复杂的非线性、时变系统。
- 灵活性高:模糊规则的制定相对灵活,可根据不同的控制对象和目标进行调整。
- 对模型依赖性低:模糊控制部分不依赖精确的数学模型,适用于难以建立精确模型的系统。
- 控制精度高:通过模糊推理优化PID参数,提高了系统的控制精度和稳定性。
模糊自适应PID控制器广泛应用于各种复杂工业过程控制,如电机调速系统、压力控制系统、智能执行器控制等,尤其适用于那些存在不确定性、非线性特性或参数时变的系统。请看下面的例子,构建了一个二阶系统模拟机械臂关节,分别用传统PID与模糊自适应 PID(F - PID)进行控制。通过设定含阶跃、斜坡变化的轨迹,仿真对比二者在位置跟踪的表现。在应对工况变化时,F-PID能够借助模糊规则动态调整参数比参数固定的传统 PID展现出更优的跟踪精度与适应性,验证了新型F-PID架构在运动控制中自主优化、抗扰的优势。
实例5-1:运动控制的模糊PID演示(源码路径:codes\5\Hu.py)
实例文件Hu.py的具体实现流程如下所示。
(1)类 PIDController 的功能是提供了一个传统比例-积分-微分(PID)控制器的实现,通过误差、误差积分和误差微分的线性组合实时计算控制量,并保持上一拍误差与积分值用于下次迭代。
class PIDController:
"""传统PID控制器"""
def __init__(self, kp, ki, kd):
self.kp = kp
self.ki = ki
self.kd = kd
self.last_error = 0
self.integral = 0
def update(self, error, dt):
self.integral += error * dt
derivative = (error - self.last_error) / dt if dt > 0 else 0
output = (self.kp * error +
self.ki * self.integral +
self.kd * derivative)
self.last_error = error
return output
(2)类 FuzzyPIDController 的功能是在传统 PID 基础上引入 Mamdani 型模糊逻辑推理,根据当前误差和误差变化率在线调整 Kp、Ki、Kd 三个参数,使控制器能够自适应不同工况。
class FuzzyPIDController:
"""模糊自适应PID控制器"""
def __init__(self, kp_range, ki_range, kd_range):
self.error = ctrl.Antecedent(np.linspace(-10, 10, 101), 'error')
self.error_rate = ctrl.Antecedent(np.linspace(-10, 10, 101), 'error_rate')
self.delta_kp = ctrl.Consequent(np.linspace(-1, 1, 101), 'delta_kp')
self.delta_ki = ctrl.Consequent(np.linspace(-0.1, 0.1, 101), 'delta_ki')
self.delta_kd = ctrl.Consequent(np.linspace(-0.5, 0.5, 101), 'delta_kd')
for var in [self.error, self.error_rate]:
var['NB'] = fuzz.trimf(var.universe, [-10, -10, -5])
var['NM'] = fuzz.trimf(var.universe, [-10, -5, 0])
var['ZE'] = fuzz.trimf(var.universe, [-5, 0, 5])
var['PM'] = fuzz.trimf(var.universe, [0, 5, 10])
var['PB'] = fuzz.trimf(var.universe, [5, 10, 10])
for var in [self.delta_kp, self.delta_ki, self.delta_kd]:
var['NB'] = fuzz.trimf(var.universe,
[var.universe[0], var.universe[0], var.universe[len(var.universe) // 2 - 1]])
var['NM'] = fuzz.trimf(var.universe, [var.universe[0], var.universe[len(var.universe) // 4],
var.universe[len(var.universe) // 2 - 1]])
var['ZE'] = fuzz.trimf(var.universe,
[var.universe[len(var.universe) // 4], var.universe[len(var.universe) // 2],
var.universe[3 * len(var.universe) // 4]])
var['PM'] = fuzz.trimf(var.universe,
[var.universe[len(var.universe) // 2], var.universe[3 * len(var.universe) // 4],
var.universe[-1]])
var['PB'] = fuzz.trimf(var.universe,
[var.universe[len(var.universe) // 2], var.universe[-1], var.universe[-1]])
self.rules = [
# kp规则
ctrl.Rule(self.error['NB'] & self.error_rate['NB'], self.delta_kp['PB']),
ctrl.Rule(self.error['NB'] & self.error_rate['ZE'], self.delta_kp['PB']),
ctrl.Rule(self.error['ZE'] & self.error_rate['ZE'], self.delta_kp['ZE']),
ctrl.Rule(self.error['PB'] & self.error_rate['ZE'], self.delta_kp['NB']),
ctrl.Rule(self.error['PB'] & self.error_rate['PB'], self.delta_kp['NB']),
# ki规则
ctrl.Rule(self.error['NB'] & self.error_rate['NB'], self.delta_ki['NB']),
ctrl.Rule(self.error['NB'] & self.error_rate['ZE'], self.delta_ki['NM']),
ctrl.Rule(self.error['ZE'] & self.error_rate['ZE'], self.delta_ki['ZE']),
ctrl.Rule(self.error['PB'] & self.error_rate['ZE'], self.delta_ki['PM']),
ctrl.Rule(self.error['PB'] & self.error_rate['PB'], self.delta_ki['PB']),
# kd规则
ctrl.Rule(self.error['NB'] & self.error_rate['NB'], self.delta_kd['PM']),
ctrl.Rule(self.error['NB'] & self.error_rate['ZE'], self.delta_kd['PB']),
ctrl.Rule(self.error['ZE'] & self.error_rate['ZE'], self.delta_kd['ZE']),
ctrl.Rule(self.error['PB'] & self.error_rate['ZE'], self.delta_kd['NB']),
ctrl.Rule(self.error['PB'] & self.error_rate['PB'], self.delta_kd['NM']),
]
self.kp_ctrl = ctrl.ControlSystem(self.rules[:5])
self.ki_ctrl = ctrl.ControlSystem(self.rules[5:10])
self.kd_ctrl = ctrl.ControlSystem(self.rules[10:])
self.kp_sim = ctrl.ControlSystemSimulation(self.kp_ctrl)
self.ki_sim = ctrl.ControlSystemSimulation(self.ki_ctrl)
self.kd_sim = ctrl.ControlSystemSimulation(self.kd_ctrl)
self.kp_min, self.kp_max = kp_range
self.ki_min, self.ki_max = ki_range
self.kd_min, self.kd_max = kd_range
self.kp = (kp_range[0] + kp_range[1]) / 2
self.ki = (ki_range[0] + ki_range[1]) / 2
self.kd = (kd_range[0] + kd_range[1]) / 2
self.last_error = 0
self.integral = 0
def update(self, error, dt):
error_rate = (error - self.last_error) / dt if dt > 0 else 0
self.kp_sim.input['error'] = error
self.kp_sim.input['error_rate'] = error_rate
self.ki_sim.input['error'] = error
self.ki_sim.input['error_rate'] = error_rate
self.kd_sim.input['error'] = error
self.kd_sim.input['error_rate'] = error_rate
try:
self.kp_sim.compute()
self.ki_sim.compute()
self.kd_sim.compute()
except:
pass
delta_kp = self.kp_sim.output['delta_kp']
delta_ki = self.ki_sim.output['delta_ki']
delta_kd = self.kd_sim.output['delta_kd']
self.kp = max(self.kp_min, min(self.kp + delta_kp, self.kp_max))
self.ki = max(self.ki_min, min(self.ki + delta_ki, self.ki_max))
self.kd = max(self.kd_min, min(self.kd + delta_kd, self.kd_max))
self.integral += error * dt
derivative = error_rate
output = (self.kp * error +
self.ki * self.integral +
self.kd * derivative)
self.last_error = error
return output, self.kp, self.ki, self.kd
(3)类 SecondOrderSystem 的功能是模拟一个质量-阻尼-弹簧二阶系统,接受输入力信号后按牛顿第二定律更新速度与位移,并返回当前位置作为被控对象输出。
class SecondOrderSystem:
"""二阶系统模拟被控对象(如机械臂关节)"""
def __init__(self, m=1.0, b=0.5, k=0.2):
self.m = m
self.b = b
self.k = k
self.position = 0.0
self.velocity = 0.0
def update(self, input_signal, dt):
acceleration = (input_signal - self.b * self.velocity - self.k * self.position) / self.m
self.velocity += acceleration * dt
self.position += self.velocity * dt
return self.position
(4)函数 run_simulation 的功能是在给定设定值曲线、总时长和步长的条件下,分别用传统 PID 与模糊 PID 控制同一个二阶系统,记录并返回时间序列、设定值、两种控制器的位置响应及各自实时参数。
def run_simulation(setpoint_func, time_span, dt):
"""运行控制系统仿真"""
pid = PIDController(kp=3.0, ki=0.2, kd=0.5)
fpid = FuzzyPIDController(kp_range=(0.5, 8.0), ki_range=(0.0, 1.0), kd_range=(0.1, 2.0))
system_pid = SecondOrderSystem()
system_fpid = SecondOrderSystem()
time_points = np.arange(0, time_span, dt)
pid_positions = []
fpid_positions = []
setpoints = []
pid_params = []
fpid_params = []
for t in time_points:
setpoint = setpoint_func(t)
setpoints.append(setpoint)
# PID控制
error_pid = setpoint - system_pid.position
control_signal_pid = pid.update(error_pid, dt)
position_pid = system_pid.update(control_signal_pid, dt)
pid_positions.append(position_pid)
pid_params.append((pid.kp, pid.ki, pid.kd))
# F-PID控制
error_fpid = setpoint - system_fpid.position
control_signal_fpid, kp, ki, kd = fpid.update(error_fpid, dt)
position_fpid = system_fpid.update(control_signal_fpid, dt)
fpid_positions.append(position_fpid)
fpid_params.append((kp, ki, kd))
return time_points, setpoints, pid_positions, fpid_positions, pid_params, fpid_params
(5)函数 setpoint_function 的功能是定义分段设定值轨迹:前 5 s 为 0,随后阶跃到 5,再阶跃到 8,最后转为斜坡信号,用于检验控制器对突变与持续变化的跟踪能力。
def setpoint_function(t):
"""设定值函数(阶跃信号 + 斜坡信号)"""
if t < 5:
return 0
elif t < 10:
return 5
elif t < 15:
return 8
else:
return 5 + 0.5 * (t - 15)
(6)函数 plot_results 的功能是将仿真结果绘制成两幅图:第一幅对比传统 PID 与模糊 PID 的位置跟踪曲线;第二幅在同一坐标系内展示两种控制器 Kp、Ki、Kd 随时间的变化。
def plot_results(time_points, setpoints, pid_positions, fpid_positions, pid_params, fpid_params):
"""绘制仿真结果"""
plt.figure(figsize=(15, 10))
# 绘制位置跟踪结果
plt.subplot(2, 1, 1)
plt.plot(time_points, setpoints, 'k--', label='设定值')
plt.plot(time_points, pid_positions, 'b-', label='PID控制')
plt.plot(time_points, fpid_positions, 'r-', label='F-PID控制')
plt.xlabel('时间 (s)')
plt.ylabel('位置')
plt.title('位置跟踪对比')
plt.legend()
plt.grid(True)
# 绘制PID参数变化
plt.subplot(2, 1, 2)
plt.plot(time_points, [p[0] for p in pid_params], 'b-', label='PID-Kp')
plt.plot(time_points, [p[0] for p in fpid_params], 'r-', label='F-PID-Kp')
plt.plot(time_points, [p[1] for p in pid_params], 'b--', label='PID-Ki')
plt.plot(time_points, [p[1] for p in fpid_params], 'r--', label='F-PID-Ki')
plt.plot(time_points, [p[2] for p in pid_params], 'b-.', label='PID-Kd')
plt.plot(time_points, [p[2] for p in fpid_params], 'r-.', label='F-PID-Kd')
plt.xlabel('时间 (s)')
plt.ylabel('参数值')
plt.title('PID参数变化对比')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
(7)函数 animate_results 的功能是创建并保存一个左右分栏的动画 GIF:左侧展示传统 PID 控制的旋转臂实时指向,右侧展示模糊 PID 的情况,同时标记目标角度,便于直观比较动态响应。
def animate_results(time_points, setpoints, pid_positions, fpid_positions):
"""创建动画展示控制效果并保存为GIF"""
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))
ax1.set_xlim(-1.2, 1.2)
ax1.set_ylim(-1.2, 1.2)
ax1.set_aspect('equal')
ax1.grid(True)
ax1.set_title('PID控制')
ax2.set_xlim(-1.2, 1.2)
ax2.set_ylim(-1.2, 1.2)
ax2.set_aspect('equal')
ax2.grid(True)
ax2.set_title('F-PID控制')
line_pid, = ax1.plot([], [], 'b-', lw=2)
target_pid, = ax1.plot([], [], 'go', markersize=10)
line_fpid, = ax2.plot([], [], 'r-', lw=2)
target_fpid, = ax2.plot([], [], 'go', markersize=10)
time_text = ax1.text(0.02, 0.95, '', transform=ax1.transAxes)
def init():
line_pid.set_data([], [])
target_pid.set_data([], [])
line_fpid.set_data([], [])
target_fpid.set_data([], [])
time_text.set_text('')
return line_pid, target_pid, line_fpid, target_fpid, time_text
def update(frame):
theta_pid = np.radians(pid_positions[frame])
theta_fpid = np.radians(fpid_positions[frame])
theta_target = np.radians(setpoints[frame])
x_pid = np.cos(theta_pid)
y_pid = np.sin(theta_pid)
x_fpid = np.cos(theta_fpid)
y_fpid = np.sin(theta_fpid)
x_target = np.cos(theta_target)
y_target = np.sin(theta_target)
line_pid.set_data([0, x_pid], [0, y_pid])
target_pid.set_data(x_target, y_target)
line_fpid.set_data([0, x_fpid], [0, y_fpid])
target_fpid.set_data(x_target, y_target)
time_text.set_text(f't = {time_points[frame]:.1f}s')
return line_pid, target_pid, line_fpid, target_fpid, time_text
ani = FuncAnimation(fig, update, frames=len(time_points),
init_func=init, blit=True, interval=20)
# 保存动画为GIF
writer = PillowWriter(fps=30) # 设置帧率
ani.save('control_animation.gif', writer=writer)
print("动画已保存为 control_animation.gif")
plt.tight_layout()
plt.show()
return ani
(8)下面代码一次性完成整个控制系统仿真的闭环流程:先调用 run_simulation在20秒内以0.05 秒步长分别运行传统PID与模糊PID对同一二阶对象的位置跟踪实验,随后用 plot_results 绘制两种算法的跟踪曲线和参数演化图,最后用 animate_results 生成并保存实时对比动画 GIF,直观展示两种控制策略在设定值阶跃与斜坡变化下的动态差异。
# 运行仿真
time_points, setpoints, pid_positions, fpid_positions, pid_params, fpid_params = run_simulation(
setpoint_function, time_span=20.0, dt=0.05)
# 绘制结果
plot_results(time_points, setpoints, pid_positions, fpid_positions, pid_params, fpid_params)
# 生成并保存动画
animate_results(time_points, setpoints, pid_positions, fpid_positions)
执行后生成的可视化图和动画清晰对比了传统 PID(蓝线)与模糊自适应 PID(红线)在同一二阶系统上的控制效果,如图5-1所示。静态图的上半幅显示设定值轨迹与两种算法的实际位置响应,下半幅实时记录 Kp、Ki、Kd 的变化曲线。
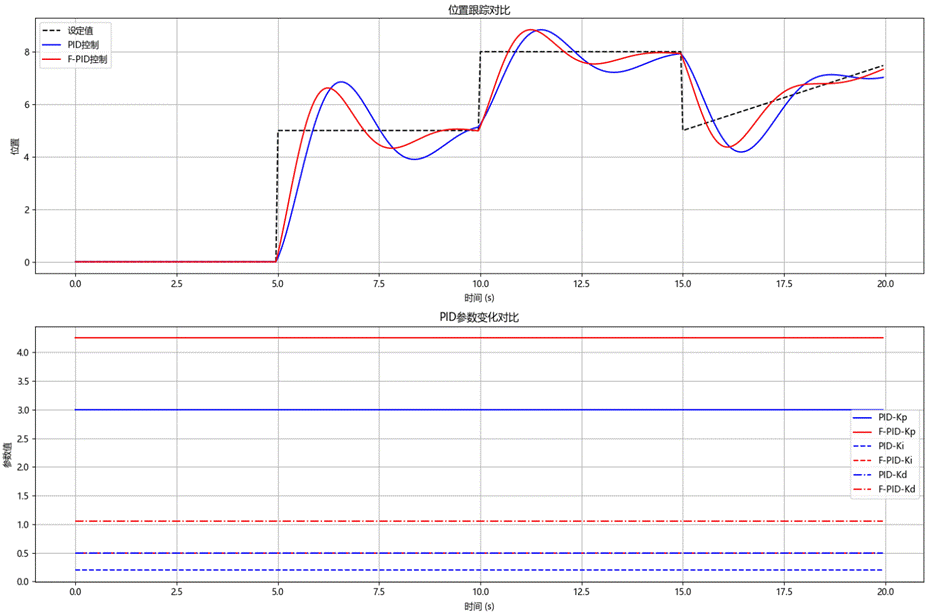
图5-1 传统 PID与模糊自适应 PID在同一二阶系统上的控制效果
另外,执行后还会创建动画文件control_animation.gif并保存到本地,如图5-2所示。动态动画则以左右双轴旋转臂形式,随时间同步演示两种控制器如何追踪目标角度,直观展示模糊 PID 在超调抑制与快速收敛上的优势。
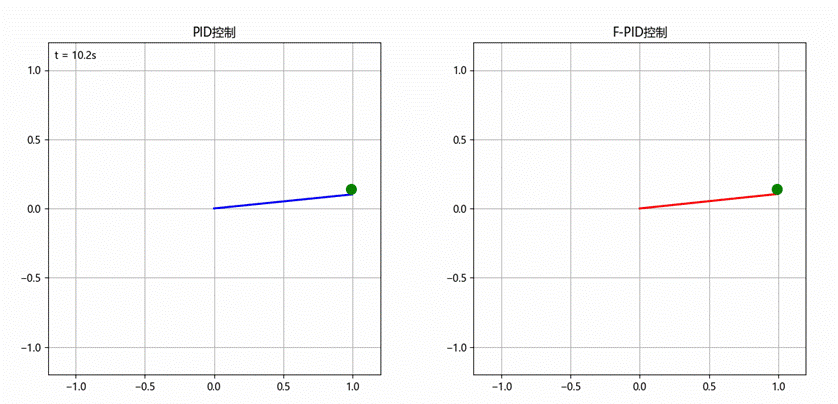
图5-2 创建的动画


























 27
27

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










