
5.2.2 数字孪生辅助调试
数字孪生辅助调试把整条PID调参流水线搬到云端或边缘服务器的高保真虚拟镜像里,形成“模型-数据-算法”闭环。它不再依赖工程师到现场“拧旋钮”,而是在数字空间完成90 %以上的调试与验证,再把一键生成的参数热插拔到真实设备。以下从孪生构建、调试流程、闭环更新、工业案例四个维度展开说明。
1. 孪生构建:从几何到控制的全栈模型
(1)机理层:使用多体动力学或有限元建立关节/电机/负载的物理方程,保留质量、阻尼、刚度、摩擦非线性。
(2)控制层:把 PLC、伺服驱动、采样周期、量化误差全部建模,PID 以 C Function-Block 形式嵌入,保证位级一致。
(3)数据层:通过 MQTT/OPC-UA 实时注入现场温度、电流、振动等传感数据,用卡尔曼滤波同步校正孪生状态,延迟 <10 ms。
(4)接口层:导出 FMU/FMI 或 ONNX 格式,供 Python、MATLAB、TwinCAT 直接调用,实现“一次建模、多平台复用”。
2. 调试流程:离线标定 → 虚拟调参 → 在线迁移
(1)离线标定
- 数字孪生先用遗传算法在1万个工况中粗筛PID区间,生成Pareto前沿(超调 vs 能耗)。
- 将结果写入“参数库”,供后续 RL 微调初始化。
(2)虚拟调参
- 场景泛化:孪生体可在5s内跑完真实8小时的温度漂移、负载扰动、电网谐波组合测试。
- 故障注入:模拟编码器掉线、执行器饱和、摩擦突变,验证 PID 的鲁棒裕度。
- 一键 HIL:孪生体直接与真实PLC对接,形成硬件在环 (HIL) 测试,确保控制周期、抖动完全一致。
(3)在线迁移
- 采用“影子模式”——孪生PID与现场PID并行运行,误差 > 阈值才切换,实现零停机热更新。
- 迁移后孪生体继续以1 Hz频率微调参数,形成“数字孪生-物理实体”的共生闭环。
3. 闭环更新:孪生体持续学习
(1)自适应网格:孪生体利用在线数据实时更新摩擦、惯量参数,网格粗化/细化自动切换,保证模型保真度> 95%。
(2)强化学习沙盒:在孪生体内运行PPO/SAC,每100 ms生成新PID增益,通过A/B测试决定是否下发到现场。
(3)边缘-云协同:边缘孪生负责毫秒级闭环,云端孪生负责小时级全局优化,两者通过增量同步压缩带宽90%。
总之,数字孪生把 PID 整定从“现场试错”升级为“云端预演、实时同步、持续优化”,在虚拟空间完成 90 % 的工况覆盖与参数验证,真正实现“零停机、低风险、全天候”的智能调试。例如下面是一个基于Python的数字孪生辅助PID例子,展示了通过构建物理系统的虚拟镜像来优化PID控制器参数的过程。这个例子模拟了一个机械臂关节的控制场景,包含物理系统、数字孪生模型、PID控制器和调试流程:
实例5-4:用物理系统的虚拟镜像来优化PID控制器参数(源码路径:codes\5\Shu.py)
实例文件Shu.py的具体实现流程如下所示。
(1)类 PhysicalSystem 的功能是模拟一个真实的物理系统,即具有转动惯量、阻尼系数、弹性系数和测量噪声的机械臂关节的二阶动力学模型,通过更新状态来反映控制输入对系统的影响,并模拟真实传感器的测量噪声。
# ---------------------- 1. 物理系统模型(实际被控对象) ----------------------
class PhysicalSystem:
"""物理系统:机械臂关节的二阶动力学模型"""
def __init__(self, mass=1.0, damping=0.5, stiffness=0.2, noise_level=0.05):
self.mass = mass # 转动惯量
self.damping = damping # 阻尼系数
self.stiffness = stiffness # 弹性系数
self.noise_level = noise_level # 测量噪声水平
# 系统状态
self.position = 0.0 # 关节位置
self.velocity = 0.0 # 关节速度
def update(self, control, dt):
"""更新物理系统状态"""
# 二阶动力学方程:mass * acceleration + damping * velocity + stiffness * position = control
acceleration = (control - self.damping * self.velocity - self.stiffness * self.position) / self.mass
# 更新状态
self.velocity += acceleration * dt
self.position += self.velocity * dt
# 添加测量噪声(模拟真实传感器)
noisy_position = self.position + np.random.normal(0, self.noise_level)
noisy_velocity = self.velocity + np.random.normal(0, self.noise_level)
return noisy_position, noisy_velocity
(2)类 DigitalTwin 的功能是创建一个与物理系统结构相同但参数可调的虚拟模型,即数字孪生体,它可以模拟物理系统的行为并在数字空间中进行参数优化,同时通过与物理系统的数据同步来修正模型偏差,确保数字孪生体与物理系统的一致性。
# ---------------------- 2. 数字孪生模型(物理系统的虚拟镜像) ----------------------
class DigitalTwin:
"""数字孪生模型:与物理系统结构相同但参数可调的虚拟模型"""
def __init__(self, mass=1.0, damping=0.5, stiffness=0.2, noise_level=0.01):
# 孪生模型参数(初始与物理系统相同,但可微调)
self.mass = mass
self.damping = damping
self.stiffness = stiffness
self.noise_level = noise_level
# 系统状态
self.position = 0.0
self.velocity = 0.0
# 模型与物理系统的偏差(可通过数据同步修正)
self.position_bias = 0.0
self.velocity_bias = 0.0
def update(self, control, dt):
"""更新数字孪生状态"""
# 二阶动力学方程(与物理系统相同)
acceleration = (control - self.damping * self.velocity - self.stiffness * self.position) / self.mass
# 更新状态
self.velocity += acceleration * dt
self.position += self.velocity * dt
# 添加轻微噪声(模拟模型不确定性)
noisy_position = self.position + np.random.normal(0, self.noise_level)
noisy_velocity = self.velocity + np.random.normal(0, self.noise_level)
# 应用偏差修正(可通过数据同步更新)
corrected_position = noisy_position + self.position_bias
corrected_velocity = noisy_velocity + self.velocity_bias
return corrected_position, corrected_velocity
def sync_with_physical(self, physical_position, physical_velocity):
"""与物理系统数据同步,更新模型偏差"""
self.position_bias = physical_position - self.position
self.velocity_bias = physical_velocity - self.velocity
(3)类 PIDController 的功能是实现一个 PID 控制器,通过计算比例、积分和微分项来生成控制输出,以调整系统的响应,同时提供参数更新接口,以便在数字孪生辅助调试过程中优化控制性能。
# ---------------------- 3. PID控制器 ----------------------
class PIDController:
"""PID控制器"""
def __init__(self, kp=0.0, ki=0.0, kd=0.0):
self.kp = kp # 比例增益
self.ki = ki # 积分增益
self.kd = kd # 微分增益
self.error_sum = 0.0 # 误差积分
self.last_error = 0.0 # 上一步误差
self.last_control = 0.0 # 上一步控制输出
def compute(self, setpoint, current_value, dt):
"""计算PID控制输出"""
# 计算当前误差
error = setpoint - current_value
# 计算误差积分和微分
self.error_sum += error * dt
error_derivative = (error - self.last_error) / dt
# 计算PID输出
control = (self.kp * error +
self.ki * self.error_sum +
self.kd * error_derivative)
# 限制控制输出范围(防止积分饱和)
control = np.clip(control, -10.0, 10.0)
# 记录当前误差用于下一次计算
self.last_error = error
self.last_control = control
return control
def update_parameters(self, kp, ki, kd):
"""更新PID参数"""
self.kp = kp
self.ki = ki
self.kd = kd
(4)函数 twin_assisted_tuning 的功能是通过数字孪生辅助调试流程来优化 PID 控制器的参数,它在数字孪生环境中测试当前 PID 参数,评估性能,并基于性能调整 PID 参数,然后将优化后的参数应用到物理系统上,记录调试过程数据,实现 PID 参数的智能优化。
# ---------------------- 4. 数字孪生辅助调试流程 ----------------------
def twin_assisted_tuning(physical_system, digital_twin, pid_controller,
setpoint=1.0, dt=0.01, tuning_steps=200):
"""数字孪生辅助PID参数调试流程"""
# 存储调试过程数据
physical_positions = []
twin_positions = []
errors = []
kp_values = []
ki_values = []
kd_values = []
# 初始PID参数(待优化)
kp, ki, kd = pid_controller.kp, pid_controller.ki, pid_controller.kd
# 调试循环
for step in range(tuning_steps):
# 在数字孪生环境中测试当前PID参数
twin_position, twin_velocity = 0.0, 0.0
twin_error_sum = 0.0
twin_pid = PIDController(kp, ki, kd)
# 模拟一个完整的响应过程(100个时间步)
for sim_step in range(100):
control = twin_pid.compute(setpoint, twin_position, dt)
twin_position, twin_velocity = digital_twin.update(control, dt)
twin_error_sum += abs(setpoint - twin_position)
# 评估性能(误差越小越好)
performance = twin_error_sum / 100
# 基于性能调整PID参数(简化的参数搜索)
if step % 10 == 0: # 每10步尝试微调参数
# 随机生成几个候选参数集
candidates = []
for _ in range(5):
# 在当前参数附近随机扰动
candidate_kp = kp + random.uniform(-0.5, 0.5)
candidate_ki = ki + random.uniform(-0.1, 0.1)
candidate_kd = kd + random.uniform(-0.1, 0.1)
# 确保参数非负
candidate_kp = max(0.0, candidate_kp)
candidate_ki = max(0.0, candidate_ki)
candidate_kd = max(0.0, candidate_kd)
candidates.append((candidate_kp, candidate_ki, candidate_kd))
# 在数字孪生中评估每个候选参数
best_performance = float('inf')
best_candidate = (kp, ki, kd)
for candidate in candidates:
test_kp, test_ki, test_kd = candidate
twin_test_pid = PIDController(test_kp, test_ki, test_kd)
test_position, test_velocity = 0.0, 0.0
test_error_sum = 0.0
for sim_step in range(100):
control = twin_test_pid.compute(setpoint, test_position, dt)
test_position, test_velocity = digital_twin.update(control, dt)
test_error_sum += abs(setpoint - test_position)
test_performance = test_error_sum / 100
if test_performance < best_performance:
best_performance = test_performance
best_candidate = candidate
# 如果找到更优参数,则更新
if best_performance < performance:
kp, ki, kd = best_candidate
pid_controller.update_parameters(kp, ki, kd)
# 在物理系统上应用当前PID参数并记录结果
control = pid_controller.compute(setpoint, physical_system.position, dt)
physical_position, physical_velocity = physical_system.update(control, dt)
# 数字孪生与物理系统数据同步
digital_twin.sync_with_physical(physical_position, physical_velocity)
# 记录数据
physical_positions.append(physical_position)
twin_positions.append(digital_twin.position)
errors.append(setpoint - physical_position)
kp_values.append(kp)
ki_values.append(ki)
kd_values.append(kd)
# 打印进度
if (step + 1) % 50 == 0:
print(f"Step {step+1}/{tuning_steps}, "
f"Current PID: Kp={kp:.2f}, Ki={ki:.2f}, Kd={kd:.2f}, "
f"Error: {abs(errors[-1]):.4f}")
return physical_positions, twin_positions, errors, kp_values, ki_values, kd_values
(5)函数 visualize_results 的功能是可视化调试结果,包括物理系统与数字孪生的位置跟踪对比、跟踪误差、PID 参数优化过程以及优化后的位置跟踪效果,通过图表直观展示数字孪生辅助调试的效果和最终优化的 PID 参数。
# ---------------------- 5. 可视化与主程序 ----------------------
def visualize_results(physical_positions, twin_positions, errors, kp_values, ki_values, kd_values, setpoint):
"""可视化调试结果"""
time_steps = len(physical_positions)
time = np.arange(time_steps) * 0.01 # 时间轴
plt.figure(figsize=(15, 10))
# 位置跟踪对比
plt.subplot(2, 2, 1)
plt.plot(time, physical_positions, 'b-', label='物理系统')
plt.plot(time, twin_positions, 'r--', label='数字孪生')
plt.axhline(y=setpoint, color='k', linestyle='--', label='目标位置')
plt.xlabel('时间 (s)')
plt.ylabel('位置')
plt.title('物理系统 vs 数字孪生位置跟踪')
plt.legend()
plt.grid(True)
# 跟踪误差
plt.subplot(2, 2, 2)
plt.plot(time, errors, 'g-')
plt.axhline(y=0, color='k', linestyle='--')
plt.xlabel('时间 (s)')
plt.ylabel('误差')
plt.title('跟踪误差')
plt.grid(True)
# PID参数变化
plt.subplot(2, 2, 3)
plt.plot(time, kp_values, 'r-', label='Kp')
plt.plot(time, ki_values, 'g-', label='Ki')
plt.plot(time, kd_values, 'b-', label='Kd')
plt.xlabel('时间 (s)')
plt.ylabel('参数值')
plt.title('PID参数优化过程')
plt.legend()
plt.grid(True)
# 最终参数效果
plt.subplot(2, 2, 4)
final_steps = min(100, time_steps)
plt.plot(time[-final_steps:], physical_positions[-final_steps:], 'b-', label='物理系统')
plt.plot(time[-final_steps:], twin_positions[-final_steps:], 'r--', label='数字孪生')
plt.axhline(y=setpoint, color='k', linestyle='--', label='目标位置')
plt.xlabel('时间 (s)')
plt.ylabel('位置')
plt.title('优化后的位置跟踪效果')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
(6)下面主程序的功能是创建物理系统、数字孪生模型和 PID 控制器实例,设置目标位置,执行数字孪生辅助调试流程,可视化调试结果,并输出最终优化的 PID 参数,展示了数字孪生辅助调试在运动控制中的完整应用过程。
if __name__ == "__main__":
# 创建物理系统(带噪声和不确定性)
physical_system = PhysicalSystem(
mass=1.0, # 物理系统质量
damping=0.6, # 物理系统阻尼(与孪生模型略有不同)
stiffness=0.2,
noise_level=0.05 # 测量噪声
)
# 创建数字孪生模型(初始参数与物理系统接近但不完全相同)
digital_twin = DigitalTwin(
mass=1.0,
damping=0.5, # 孪生模型阻尼(与物理系统有偏差)
stiffness=0.2,
noise_level=0.01 # 模型噪声(通常小于物理系统)
)
# 创建PID控制器(初始参数不佳)
pid_controller = PIDController(kp=1.0, ki=0.1, kd=0.05)
# 目标位置
setpoint = 1.0 # 弧度
# 执行数字孪生辅助调试
print("开始数字孪生辅助PID参数调试...")
physical_positions, twin_positions, errors, kp_values, ki_values, kd_values = twin_assisted_tuning(
physical_system, digital_twin, pid_controller,
setpoint=setpoint, dt=0.01, tuning_steps=200
)
# 可视化结果
visualize_results(physical_positions, twin_positions, errors, kp_values, ki_values, kd_values, setpoint)
# 输出最终优化的PID参数
print(f"\n优化后的PID参数: Kp={kp_values[-1]:.2f}, Ki={ki_values[-1]:.2f}, Kd={kd_values[-1]:.2f}")
执行后绘制四个可视化图(图5-8),具体说明如下所示。
- 位置跟踪对比图:展示了物理系统和数字孪生系统在位置跟踪方面的表现,其中蓝色实线代表物理系统的位置变化,红色虚线代表数字孪生的位置变化,黑色虚线表示目标位置。此图用于比较两者的跟踪精度和响应特性。
- 跟踪误差图:显示了物理系统在跟踪目标位置过程中的误差变化,纵轴为误差值,横轴为时间。该图用于评估控制系统的准确性,理想情况下误差应尽可能接近零。
- PID参数优化过程图:描绘了在调试过程中PID控制器的比例(Kp)、积分(Ki)和微分(Kd)增益的变化情况。通过观察这些参数的变化趋势,可以了解参数优化的动态过程。
- 优化后的位置跟踪效果图:在调试结束后,展示了物理系统和数字孪生系统使用最终优化的PID参数进行位置跟踪的效果。此图用于验证优化后的PID参数是否显著提升了系统的控制性能。
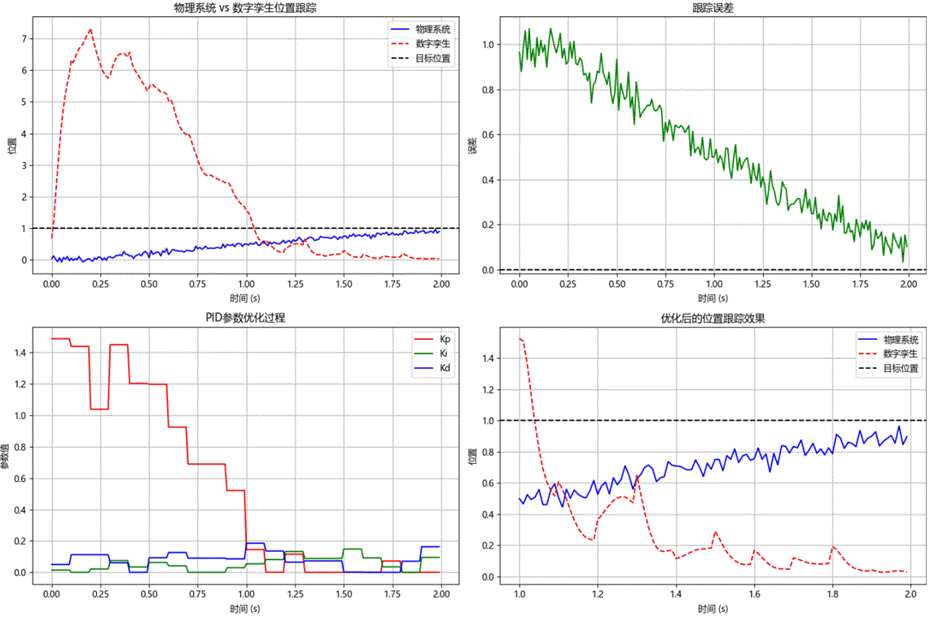
图5-8 可视化图






















 872
872

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










