首先要知道a^3+b^3=(a+b)(a^2-ab+b^2)
则1/x^3+1=1/(x+1)(x^2-x+1),到这儿应该把分母乘积的关系分开,
令1/x^3+1=1/(x+1)(x^2-x+1)=A/(x+1)+Bx+C/x^2-x+1
通过上式,两边相等解出A=1/3 B=负1/3 C=2/3
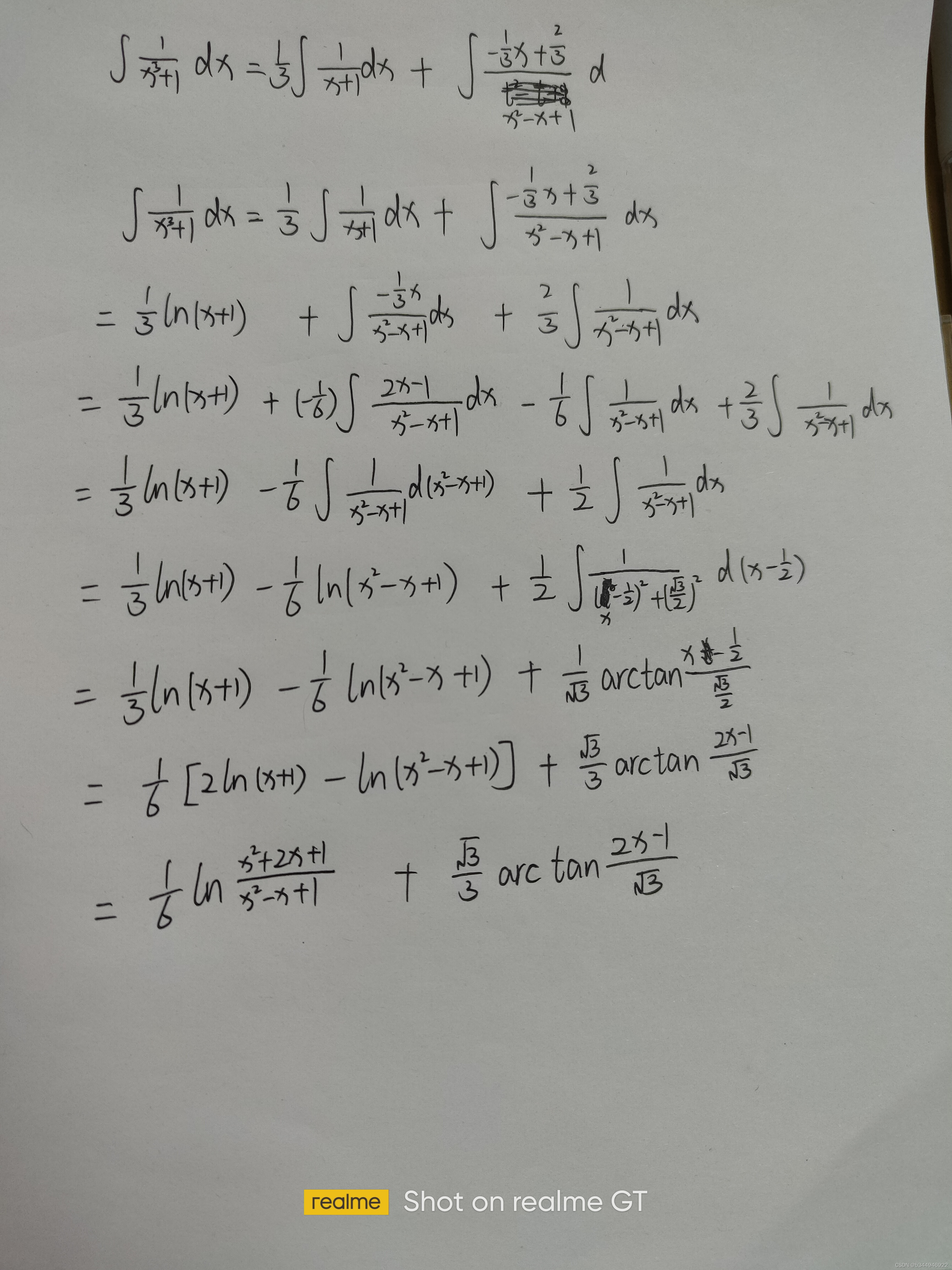
首先要知道a^3+b^3=(a+b)(a^2-ab+b^2)
则1/x^3+1=1/(x+1)(x^2-x+1),到这儿应该把分母乘积的关系分开,
令1/x^3+1=1/(x+1)(x^2-x+1)=A/(x+1)+Bx+C/x^2-x+1
通过上式,两边相等解出A=1/3 B=负1/3 C=2/3
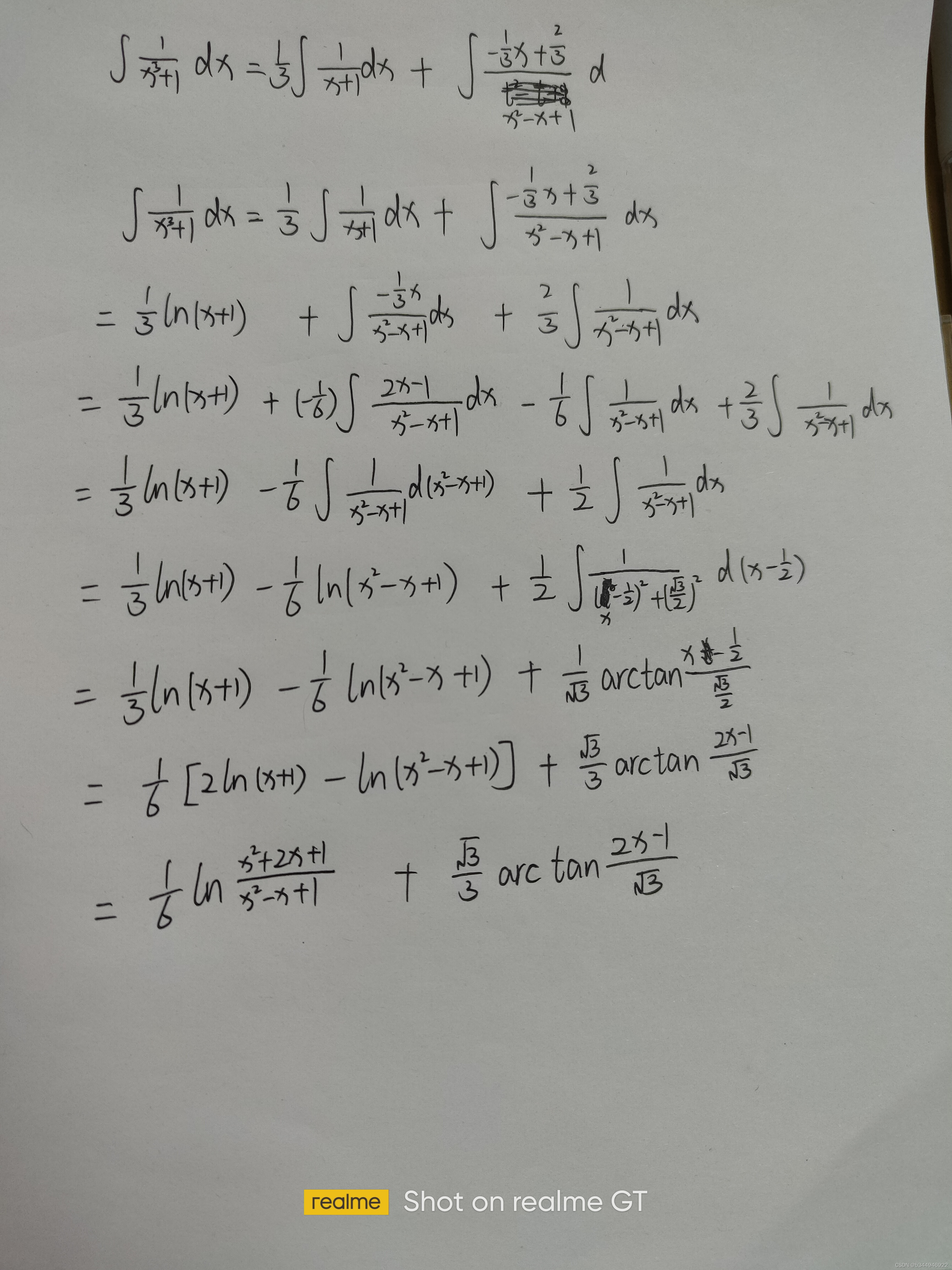
 5113
5113
 2114
2114
 6283
6283
 3231
3231

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


