弦理论的基本数学结构

        原创：项道德（daode3056）

        运动粒子的轨迹，大多是符合三角函数、双曲函数数学描述的，在平面中的描述是二维，在空间中的描述是三维，带时间、空间的描述是四维，三维与四维的描述最好是3D动画，重要的是，这种描述必须是按物理规律与公式的，这里重点是利用归一化Hermite多项式来构造二维运动的轨道运动模型【p,q取0---10阶,u取-PI到PI】，即：

Xp = HermitePoly0to10(p, u);

Yp = HermitePoly0to10(q, u);

        Hermite多项式来自一维谐振子偏微分方程的解，各阶正符合能级分布，所以归一化Hermite多项式是大自然的语言，是广义傅里叶级数的正交基。0--10阶的多项式如下：

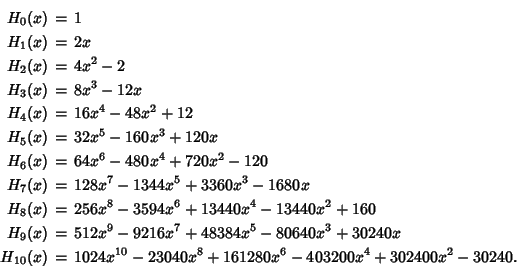
正交归一化等式： 

现在，我们只考虑它的极简模式：平面的二维运动，用程序的图像输出以描述各阶的曲线，现分享给大家，以方便各们深入探究量子规律：

再在三维以上配合自旋、角动量计算，加入Pauli、Dirac矩阵，将有许多内容要研究。

在三角函数方面，主要是稳定态的轨迹，有理曲线簇呈现的花样如下：

这类曲线，大多被用于美术与工程设计中。

Hermite多项式另一变换后的曲线，可用于神经网络与路径生成：

原创：项道德（daode3056，微信：daode1212）