【强化学习的数学原理】课程笔记（二）——贝尔曼公式

说明：本内容为个人自用学习笔记，整理自b站西湖大学赵世钰老师的 【强化学习的数学原理】课程，特别感谢老师分享讲解如此清楚的课程。

一个概念（state value）+ 一个工具（the bellman equation）

1. return 的重要性

• return could be used to evaluate policies
• return 的计算，bootstrapping：从自己出发迭代计算（bellman equation）

2. state value

• signal-step process

$$S_t\stackrel{A_t}{⟶}{R}_{t+1},S_{t+1}$$

在 $t$ 时刻处于状态 $S_t$，采取行动 $A_t$ 跳转到状态 $S_{t+1}$，得到的收益为 $R_{t+1}$，有时也记作 $R_t$，含义相同，只是习惯问题。

• multi-step trajectory
  $$S_t\stackrel{A_t}{⟶}{R}_{t+1},S_{t+1}\stackrel{A_{t+1}}{⟶}{R}_{t+2},S_{t+2}\stackrel{A_{t+2}}{⟶}{R}_{t+3},S_{t+3}\cdots$$
  discounted return（$G_t$ 是随机变量）:
  $$G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+\cdots$$

• $G_t$ 的期望被定义为 state-value function，简称为 state value
  $$v_{\pi }(s)=\mathbb{E}[G_t|S_t=s]$$

  • 关于s的函数
  • 基于策略 $\pi$的函数， $v(\pi ,s)$记为 $v_{\pi }(s)$
  • $v_{\pi }(s)$ 越大，代表策略越好！

• return 和 state value 的区别

  • return 针对单个 trajectory，state value 针对多个 trajectory 求平均。
  • 当 $\pi (a|s),p(r|s,a),p(s^{\prime }|s,a)$ 是确定的时候，return = state value

3. bellman equation

Bellman equation 描述了所有的values和state之间的关系！

3.1 Bellman equation 的推导

对于一个随机的trajectory，
$$S_t\stackrel{A_t}{⟶}{R}_{t+1},S_{t+1}\stackrel{A_{t+1}}{⟶}{R}_{t+2},S_{t+2}\stackrel{A_{t+2}}{⟶}{R}_{t+3},S_{t+3}\cdots$$
return $G_t$
$$G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+\cdots =R_{t+1}+\gamma G_{t+1}$$
so
$$\begin{array}{rl}{v}_{\pi }(s)& =\mathbb{E}[G_t|S_t=s]\\ & =\mathbb{E}[R_{t+1}+\gamma G_{t+1}|S_t=s]\\ & =\mathbb{E}[R_{t+1}|S_t=s]+\gamma \mathbb{E}[G_{t+1}|S_t=s]\end{array}$$
分别计算上述两项，有,

• $\mathbb{E}[R_{t+1}|S_t=s]$
  $$\begin{array}{rl}\mathbb{E}[R_{t+1}|S_t=s]& =\sum _a\pi (a|s)\mathbb{E}[R_{t+1}|S_t=s,A_t=a]\\ & =\sum _a\pi (a|s)\sum _{r}p(r|s,a)r\end{array}$$

  • 在状态s可以采取多个action，采取 a 的概率为 $\pi (a|s)$，获得的value为 $\mathbb{E}[R_{t+1}|S_t=s,A_t=a]$，从状态s出发采取action a获得的 return 为 $p(r|s,a)r$
  • This is the mean of immediate rewards

• $\mathbb{E}[G_{t+1}|S_t=s]$
  $$\begin{array}{rl}\mathbb{E}[G_{t+1}|S_t=s]& =\sum _{s^{\prime }}\mathbb{E}[G_{t+1}|S_t=s,S_{t+1}=s^{\prime }]p(s^{\prime }|s)\\ & =\sum _{s^{\prime }}\mathbb{E}[G_{t+1}|S_{t+1}=s^{\prime }]p(s^{\prime }|s)\\ & =\sum _{s^{\prime }}{v}_{\pi }(s^{\prime })p(s^{\prime }|s)\\ & =\sum _{s^{\prime }}{v}_{\pi }(s^{\prime })\sum _{a}p(s^{\prime }|s,a)\pi (a|s)\end{array}$$

  • 从状态 s 出发得到的下一时刻 return 的mean，也就是future rewards
  • $\mathbb{E}[G_{t+1}|S_{t+1}=s^{\prime }]$ 去掉 $S_t=s$是因为已经知道下一时刻的状态是s’，用到了Markov 属性，得到的值为state value
  • 从s到s’同样有多种action，采取action a的概率为 $\pi (a|s)$，选择该action从s跳到s’的概率为$p(s^{\prime }|s,a)$

因此，得到 bellman equation
$$\begin{array}{rl}{v}_{\pi }(s)& =\mathbb{E}[R_{t+1}|S_t=s]+\gamma \mathbb{E}[G_{t+1}|S_t=s]\\ & =\underset{meanofimmediaterewards}{\underbrace{\sum _a\pi (a|s)\sum _{r}p(r|s,a)r}}+\underset{meanoffuturerewards}{\underbrace{\gamma \sum _{s^{\prime }}{v}_{\pi }(s^{\prime })\sum _{a}p(s^{\prime }|s,a)\pi (a|s)}}\\ & =\sum _a\pi (a|s)\left(\sum _{r}p(r|s,a)r+\gamma \sum _{s^{\prime }}p(s^{\prime }|s,a)v_{\pi }(s^{\prime })\right),\forall s\in S.\end{array}$$

• 描述了不同 state 的 state-value 之间的关系；
• 包含 immediate 和 future 两部分
• 是方程组，每个 state 都有一个方程。
• $\pi (a|s)$ 是给定的策略，求解方程组叫做 policy evaluation
• $p(r|s,a)$ 和 $p(s^{\prime }|s,a)$ is dynamic model，存在可知和不可知两种情况！

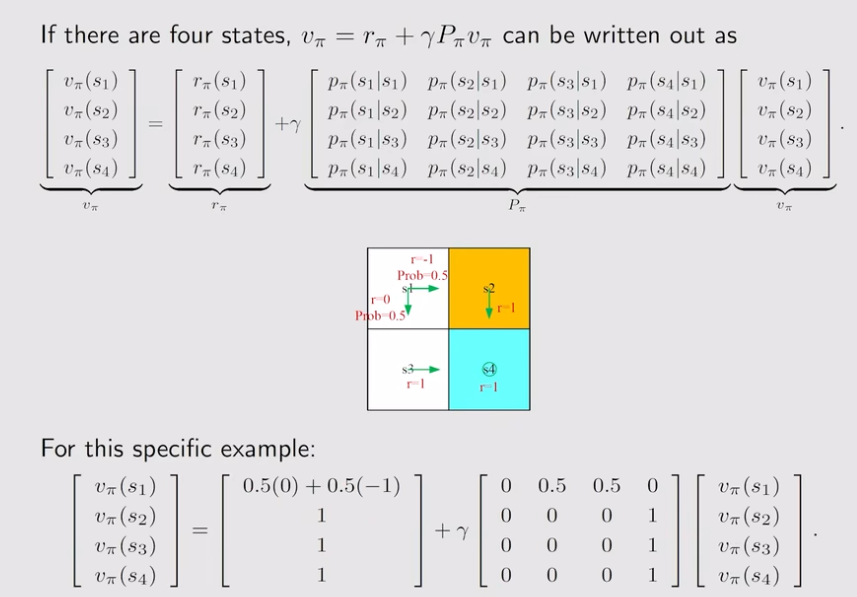
一个例子

直观上不用贝尔曼公式也可以直接写出上述结果！

计算出 state values 之后通过该值可以改进策略，最终得到最优策略。

3.2 Matrix-vector form of the Bellman Equation

$$\begin{array}{rl}{v}_{\pi }(s)& =\mathbb{E}[R_{t+1}|S_t=s]+\gamma \mathbb{E}[G_{t+1}|S_t=s]\\ & =\sum _a\pi (a|s)\sum _{r}p(r|s,a)r+\gamma \sum _{s^{\prime }}{v}_{\pi }(s^{\prime })\sum _{a}p(s^{\prime }|s,a)\pi (a|s)\\ & \stackrel{def}{=}{r}_{\pi }(s)+\gamma \sum _{s^{\prime }}p(s^{\prime }|s)v_{\pi }(s^{\prime })\end{array}$$

对于 $\forall s_i\in S$ ，
$$v_{\pi }(s_i)=r_{\pi }(s_i)+\gamma \sum _{s_j}p(s_j|s_i)v_{\pi }(s_j)$$
Matrix-vector form
$$v_{\pi }=r_{\pi }+\gamma P_{\pi }{v}_{\pi }$$
其中，$v_{\pi }\in R^n,r_{\pi }\in R^n,P_{\pi }\in R^{n\times n},[P_{\pi }{]}_{ij}=p_{\pi }(s_j|s_i)$

3.3 利用 Bellman Equation 求解 State values

给定一个策略，求解出对应的 state values 叫做 policy evaluation，这是找出更优策略的基础。

方法一：涉及到矩阵求逆，计算复杂，不使用。
$$v_{\pi }=(I-\gamma P_{\pi }{)}^{-1}{r}_{\pi }$$
方法二：利用迭代策略解决
$$v_{k+1}=r_{\pi }+\gamma P_{\pi }{v}_k$$
随机给定初值，从 $v_0$ 开始不断迭代，可以证明，当 $k \rightarrow \infty $ 时，$ v_{k}$ 就会收敛到 $v_{\pi }$

4. Action value

State value: 从一个状态出发，agent得到的average return。

Action value: 从一个状态出发，采取一个action得到的average return。

关注action value 的目的在于评估action的好坏。action value 值越大，说明该采取action越好。

定义：
$$q_{\pi }(s,a)=\mathbb{E}[G_t|S_t=s,A_t=a]$$

• $q_{\pi }(s,a)$ 是关于 $s,a$ 的函数
• $q_{\pi }(s,a)$ 基于策略 $\pi$

Action value 和 State value 在数学表达式之联系：
$$\begin{array}{rl}{v}_{\pi }(s)& =\mathbb{E}[G_t|S_t=s]\\ & =\sum _a\mathbb{E}[G_t|S_t=s,A_t=a]\\ & =\sum _a{q}_{\pi }(s,a)\pi (a|s)\\ & =\sum _a\left[\sum _{r}p(r|s,a)r+\gamma \sum _{s^{\prime }}p(s^{\prime }|s,a)v_{\pi }(s^{\prime })\right]\pi (a|s)\end{array}$$
从而有，
$$q_{\pi }(s,a)=\sum _{r}p(r|s,a)r+\gamma \sum _{s^{\prime }}p(s^{\prime }|s,a)v_{\pi }(s^{\prime })$$
上式给出了计算action value的一种方法！