用傅里叶变换分析股票曲线的周期性和波动性

 自己开发了一个股票智能分析软件，功能很强大，需要的点击下面的链接获取：

https://www.cnblogs.com/bclshuai/p/11380657.html

用傅里叶变换分析股票的周期性

目录

1      傅里叶变换... 1

2      傅里叶变换对股票曲线进行周期性分析... 2

3      总结... 4

4      视频介绍说明... 4

1        傅里叶变换

傅里叶是法国著名的数学家和物理学家，他提出的傅里叶变换可以将一条无法看出规律和周期性的曲线分解成无数个周期信号的叠加。例如将一条杂乱无章的曲线分解为很多个周期性曲线，选取5条幅值最大的周期性曲线，作为这条曲线的主要周期曲线，去除其他幅值比较小的周期曲线。如下图所示。

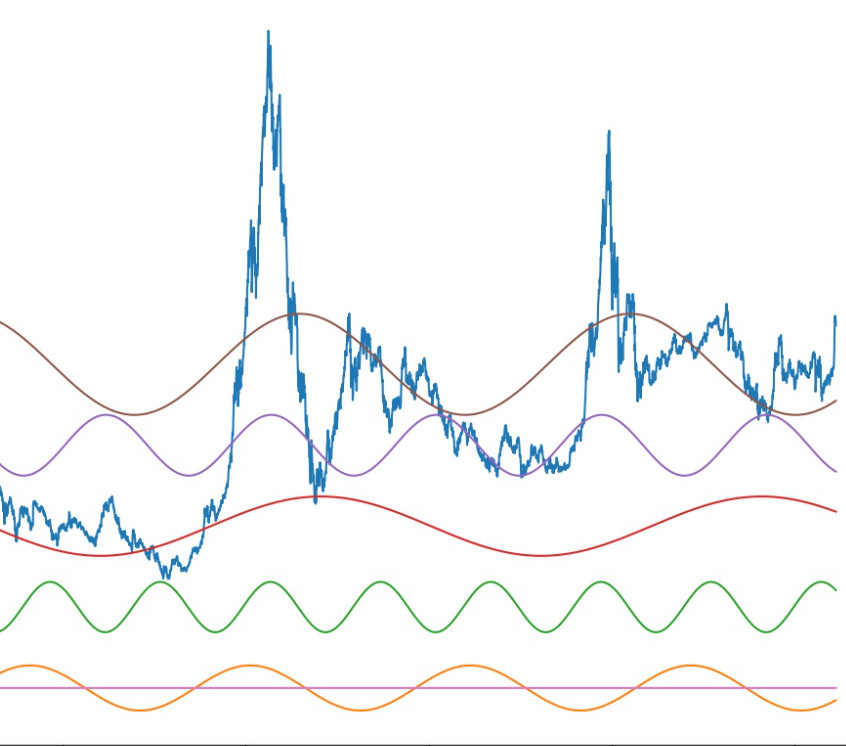
图1傅里叶曲线分解

我们将五条周期性曲线进行合成，就可以得到一条与原曲线非常接近，但是已经和原来曲线有相同的变化趋势和波动周期。可见傅里叶变换具有滤波和周期性分析功能，可以将杂乱无章的曲线分解为多个周期曲线的叠加，从而去分析曲线的周期性。去除幅值较小的波动信号，达到滤波降噪的作用。

 

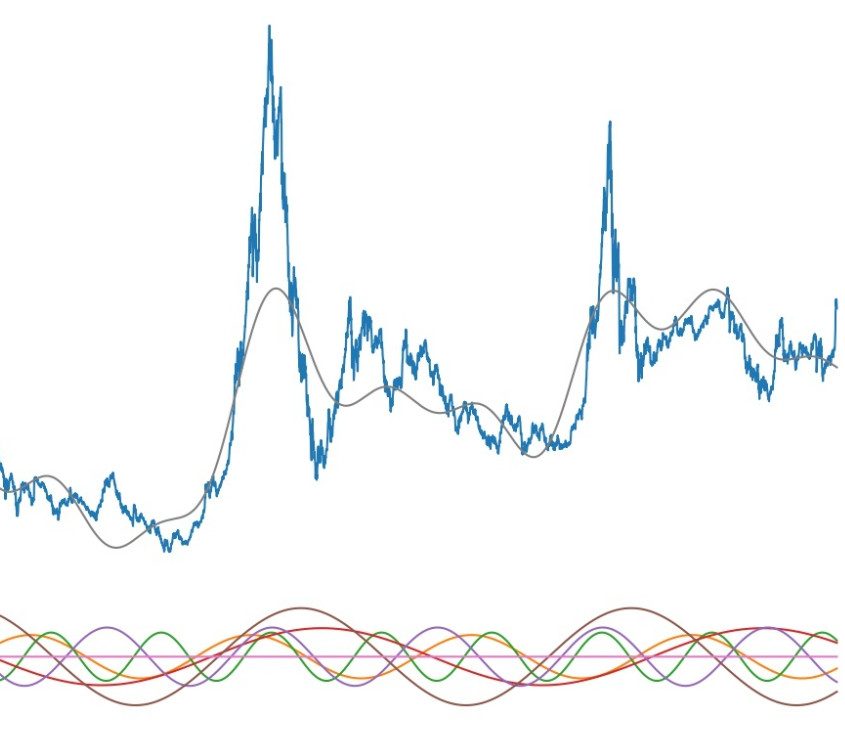
图2傅里叶曲线合成

我们可以采用傅里叶变换去分析股票曲线的周期性。

2        傅里叶变换对股票曲线进行周期性分析

股票曲线通常都是上下波动的，从长时间范围来看具有一定的周期性，但是很难找到股票曲线的周期性规律，更无法判断股票的波动周期。通过傅里叶变换可以方便的将股票曲线进行分解，并且能够得到不同周期曲线的波动周期，对分析股票的周期性具有一定的参考价值。如下图所示，将海康威视近三个月数据进行波动性分析，黑色线表示股票曲线，下面6条周期曲线是分解之后的周期曲线。短期来看股票曲线在平衡点62元附近周期震荡，震荡的上下幅值是8元，如果股票价格在54元位置附近反弹，则说明会进入下一个波动周期。

 

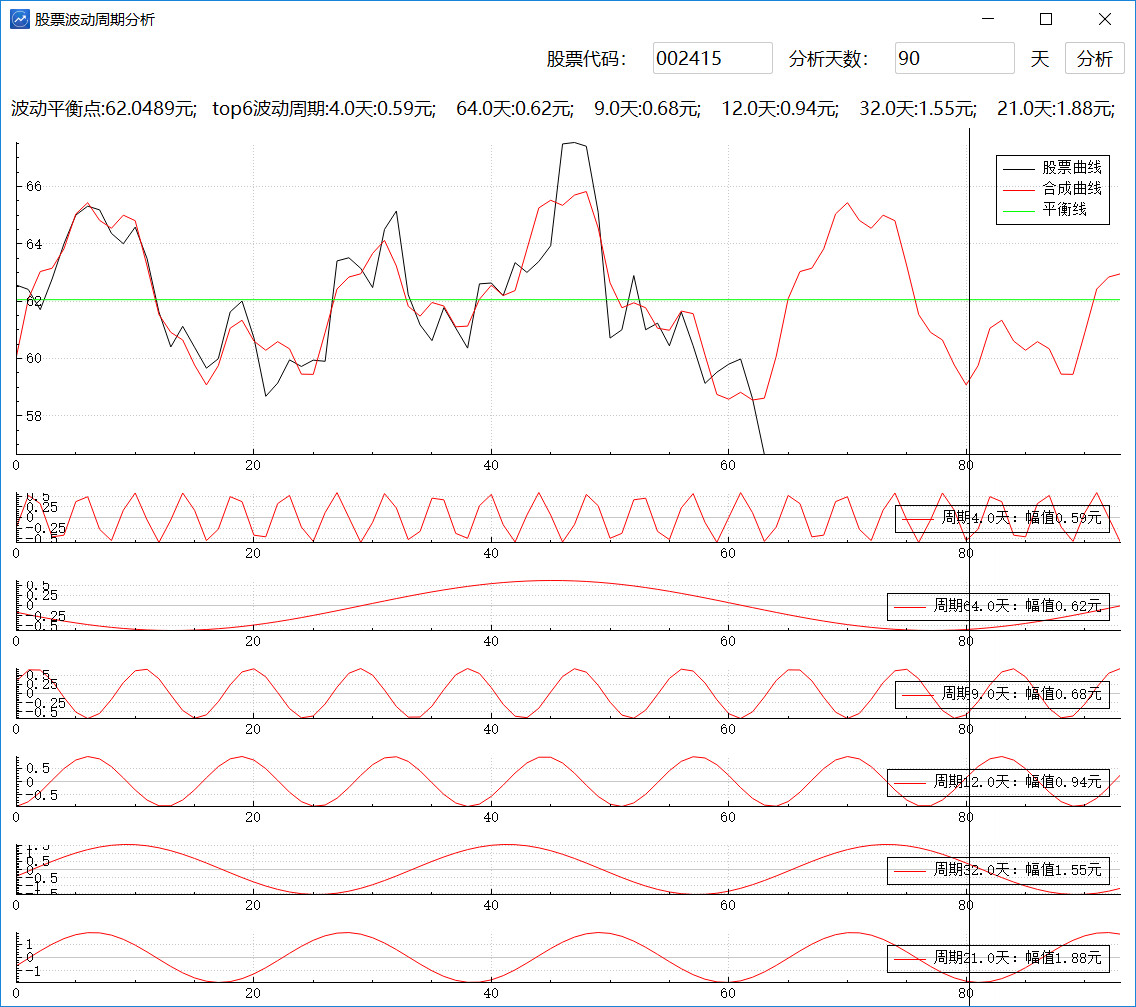
图3 近90天股票曲线周期分析

将分析天数改为300，得到近一年股票数据周期性分析如下图所示，从长期看，股票曲线有下行趋势，如果突破短期的震荡波动临界点54元，则有可能会下跌到45元左右。

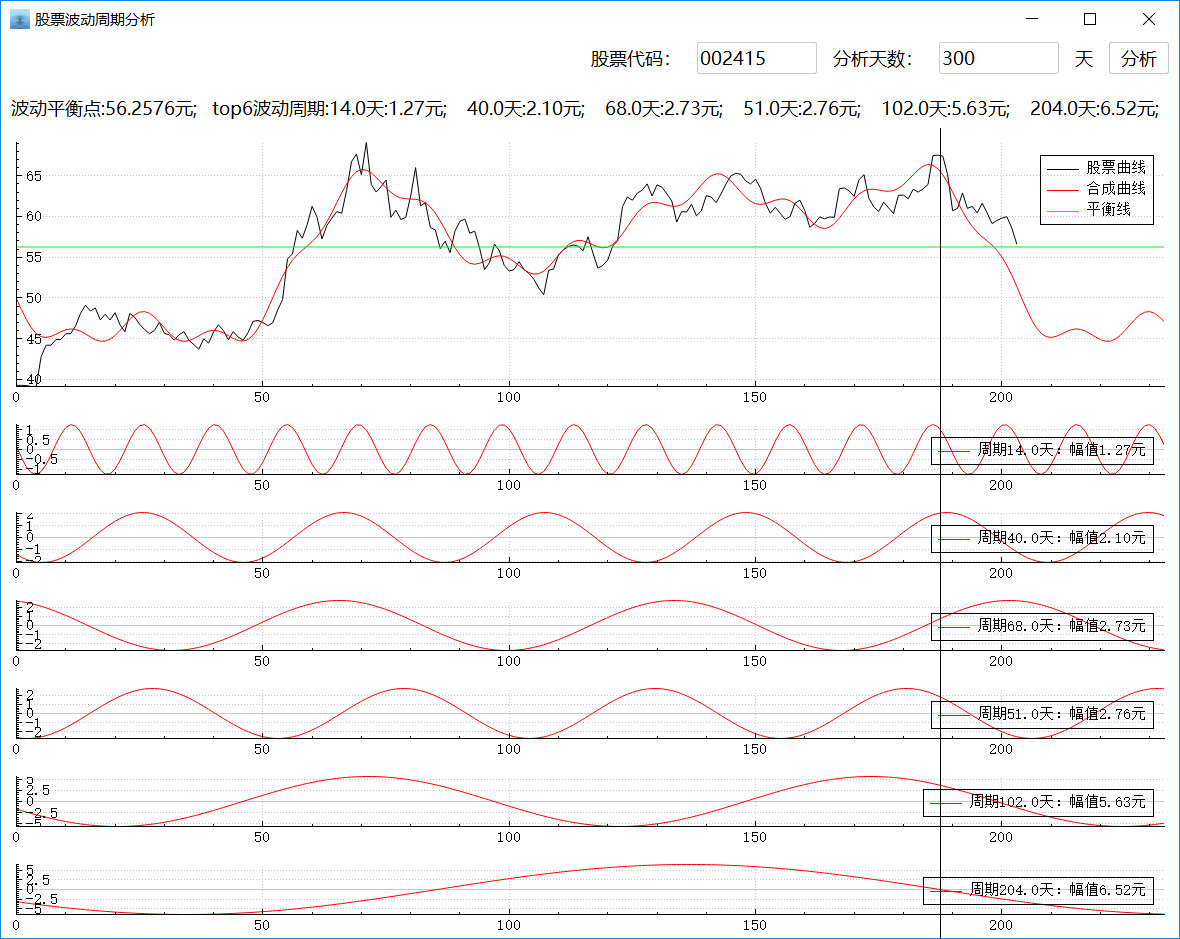
图4 近300天股票曲线周期分析

3        总结

傅里叶变化可以根据历史数据分析股票曲线的周期性，可以从长期和短期来查看股票曲线的波动周期。本软件提供的波动性分析，只能提供参考价值，不能完全按照曲线波动性进行交易，股市变化风云莫测，需慎之又慎。

4        下载地址

https://www.cnblogs.com/bclshuai/p/11380657.html