有趣的数学 什么是最速曲线？原理是什么？

        最速曲线，从字面上理解，就是“速度”最快的曲线，这里的“速度”是指平均速度、瞬时速度，抑或是速率。物理上有一个著名的最速落径问题。竖直平面内，不在同一铅垂线上的两个固定点之间的许多条曲线路径中，能使质点以最短的时间从高位置点到低位置点自由落下的那条曲线，称为最速落径，是一条旋轮线。

        如图所示，A点坐标（x1，y1），B点坐标（x2，y2），质点从A点沿曲线无摩擦下滑到B点，我们以A点同时作为零势能点和坐标原点，质点（x，y）代表其运动轨迹。

        根据能量守恒定律，不难得出质点下滑的瞬时速率为： 

        利用弧长公式得到下滑的总时间为：

        下面需要对时间求极值，以得到最短时间对应的y的方程，利用欧拉方程求解，最后得到：

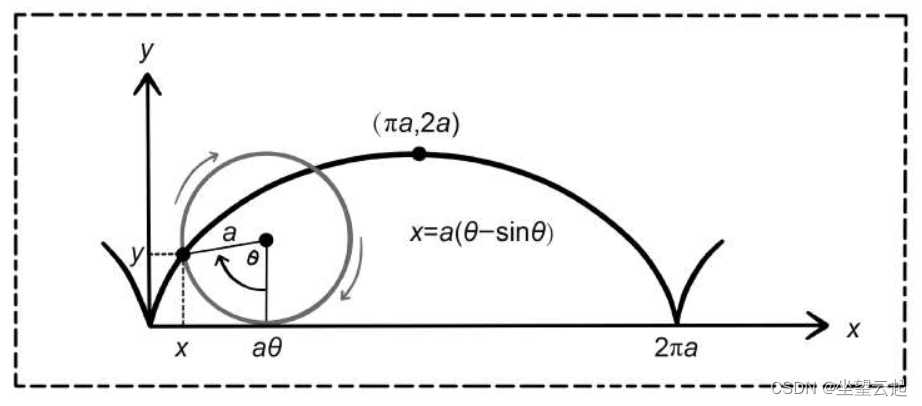
        此参数方程对应的旋轮线即为“最速曲线”。关于欧拉方程的详细求解，可以参考卢圣治主编的《理论力学基本教程》（第二版）180～187页。