swish激活函数

最新推荐文章于 2025-02-28 11:53:45 发布
最新推荐文章于 2025-02-28 11:53:45 发布
阅读量2.3w 收藏 39
点赞数 21
分类专栏： 深度学习
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/bblingbbling/article/details/107105648
版权

swish激活函数

函数公式

在这里插入图片描述

函数图像

当 β \beta β取不同的值时，函数图像如下：
在这里插入图片描述
当 β \beta β = 0时，Swish激活函数变为线性函数 f(x) = x 2 \frac{x}{2} 2x​，
当 β \beta β = ∞ \infty ∞ 时，Swish激活函数变为0或x，相当于Relu，
所以，Swish函数可以看作是介于线性函数与ReLU函数之间的平滑函数。
——————————————————————————————————
Swish函数的求导过程为：
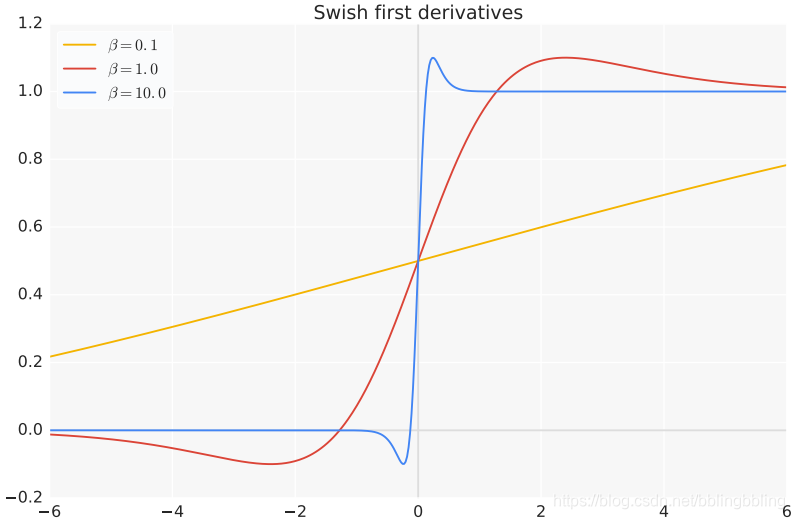
在这里插入图片描述
导数图像如下：
在这里插入图片描述

函数特点

1.Swish函数和其一阶导数都具有平滑特性；
2.有下界，无上界，非单调。

对比mish激活函数

mish激活函数参考：mish激活函数
函数图像对比如下：
在这里插入图片描述

机器学习笔记 - Swish激活函数的定义和优势
学以致用 知行合一
12-20 1439
首先，Swish 是像 ReLU、sigmoid 和 tanh 一样的非线性函数，使神经网络能够对输入和输出之间的复杂关系进行建模。非线性函数对于深度学习的工作至关重要，因为它们能够捕获和表示复杂的模式。 与 ReLU 等其他常用激活函数相比，Swish 具有独特的形状。它的形状更像是 sigmoid 函数，随着输入值的增加，输出平滑且逐渐增加。此功能使 Swish 在处理各种输入方面更具适应性和效率。
机器学习中的Swish激活函数
BxuqBlockchain的博客
10-10 780
Swish激活函数是由Google研究员Ramachandran等人在2017年提出的，它具有一定的自适应性，能够根据输入数据的范围自动调整激活函数的形状。Swish函数的输出值在[-x/2, +∞)范围内，相对于其他激活函数如ReLU，它具有更平滑的曲线，有助于减少梯度消失的问题，并提高模型的泛化能力。Swish是一种常用的机器学习中的激活函数，它在神经网络中广泛应用于提高模型的性能。使用合适的激活函数是设计高效神经网络的重要步骤之一，Swish激活函数提供了一种有效的选择。是Sigmoid函数，
神经网络中的激活函数——Swish函数
Seu_Jason的博客
05-17 4198
本文介绍了Swish函数
神经网络 - 激活函数（Swish函数、GELU函数）
最新发布
分享技术人生的学习笔记和过往心得，与志同道合者共同进步
02-28 1822
本文我们学习了神经网络的两种激活函数，分别是Swish函数和GELU函数，为了更好的理解GELU函数，还附加了概率密度函数和累积分布函数的介绍。知识的学习，有时晦涩难懂，但总归需要日积月累、慢慢消化，希望跟我一样正在学习神经网络的同学，不要放弃，持之以恒，向着目标勇敢出发！
激活函数Swish
August-us的博客
05-21 3万+
激活函数Swish系列文章：   Swish函数先对来说是比较新的一些激活函数，算是由之前的激活函数复合而成出来的。也是由Google提出的，毕竟资力雄厚，承担的起搜索的任务。而且这个算法感觉曝光率还算比较高，就在这里整理一下，同时后面的文章也会再次提到这个函数。   对前面的激活函数有了一定的基础之后，理解Swish激活就容易很多了，Swish函数的表达式是f(x)=x⋅σ(x)f(x)=x·\sigma(x)f(x)=x⋅σ(x)，σ(x)\sigma(x)σ(x)就是sigmoid函数。因为sigmo
Google提出的新型激活函数:Swish
weixin_30785593的博客
11-26 457
简介 Swish是Google在10月16号提出的一种新型激活函数,其原始公式为:f(x)=x * sigmod(x),变形Swish-B激活函数的公式则为f(x)=x * sigmod(b * x),其拥有不饱和,光滑,非单调性的特征,而Google在论文中的多项测试表明Swish以及Swish-B激活函数的性能即佳,在不同的数据集上都表现出了要优于当前最佳激...
Swish 激活函数
weixin_44012667的博客
12-06 1578
Swishxx⋅σx1e−xx​其中，σxσx1e−x1​Swish 激活函数在深度学习中的一些应用已经展示了其优势，特别是在神经网络的训练过程中。
【激活函数】Swish激活函数详解
Roaddd的博客
03-14 1万+
Swish：Self-gated activation function（2017） Swish图像： Swish公式： 当β=1 时： Swish导数： Swish特点：
Swish、ARiA、E-Swish激活函数
weixin_38190702的博客
07-12 876
Swish/ARiA/E-Swish激活函数简介
基于Swish激活函数的人脸情绪识别的深度学习模型研究.pdf
08-18
Swish在设计上引入了一个轻量级的非线性项，它和输入的乘积使得Swish激活函数拥有平滑的单侧抑制特性，这在理论上和实践中都证明了Swish激活函数的优越性。研究显示，Swish激活函数不仅在许多基准测试上性能优于ReLU...
激活函数Swish（ICLR 2018）
00000cj的博客
03-04 1194
本文提出用自动搜索技术来寻找新的激活函数。结合穷举和基于强化学习的搜索，作者发现了许多新的激活函数。作者还通过对找到的最优激活函数的经验评估来验证搜索的有效性。实验表明，找到的最优激活函数 \(f(x)=x\cdot siogmoid(\beta x)\)，作者称之为 \(Swish\)，在许多具有挑战性的数据集上，效果都优于ReLU。
谷歌swish激活函数
qq_43258953的博客
11-13 1496
Swish是Google17年在10月16号提出的一种新型激活函数,其原始公式为:f(x)=x * sigmod(x),变形Swish-B激活函数的公式则为f(x)=x * sigmod(b * x),其拥有不饱和,光滑,非单调性的特征。 f(x)=x⋅sigmoid(βx) β是个常数或可训练的参数.Swish 具备无上界有下界、平滑、非单调的特性。Swish 在深层模型上的效果优于 ReLU。...
机器学习中的数学——激活函数（八）：Swish函数
热门推荐
冯·诺依曼
10-06 3万+
Swish 的设计受到了 LSTM 和高速网络中gating的sigmoid函数使用的启发。我们使用相同的gating值来简化gating机制，这称为self-gating。 Swish(x)=x∗Sigmoid(x)\text{Swish}(x)=x*Sigmoid(x)Swish(x)=x∗Sigmoid(x) self-gating的优点在于它只需要简单的标量输入，而普通的gating则需要多个标量输入。这使得诸如Swish之类的self-gated激活函数能够轻松替换以单个标量为输入的激活函数（如：
详解激活函数Swish
大脸猫的博客
11-23 1万+
深层神经网络激活函数的选择对网络的训练动力学和任务性能有着重要的影响。目前，最成功和广泛使用的激活函数是矫正线性单元(ReLU) ，它是 f (x) = max (0，x)。虽然有人提出了各种替代 ReLU的办法，但由于收益不一致，没有一种办法能够取代它。因此，谷歌大脑团队提出了一个名为 Swish 的新激活函数，简称 f (x) = x s (x)。他们的实验表明，在一些具有挑战性的数据集上，Swish 比 ReLU 在更深层次的模型上工作得更好。例如，只需简单地用 Swish 单位替换 ReLUs，M.
激活函数(ReLU, Swish, Maxout)
weixin_30950607的博客
02-18 3077
神经网络中使用激活函数来加入非线性因素，提高模型的表达能力。 ReLU(Rectified Linear Unit,修正线性单元) 形式如下: \[ \begin{equation} f(x)= \begin{cases} 0, & {x\leq 0} \\\\ x, & {x\gt 0} \end{cases} \end{equation} \] ReLU公式近似推导::...
激活函数Swish和Hardswish简介
码农1479的博客
03-12 2万+
Swish激活函数和Hardswish激活函数学习笔记。
激活函数 05 ——Swish
Software Engineer、Artificial Intelligent
02-10 655
Swishxx⋅σβx其中σz1e−z1​原始版本中 β=1，后续研究发现可训练参数β能获得更好效果。该函数结合了ReLU的线性响应特性和Sigmoid的平滑特性。建议从固定 β=1 开始，当模型参数量>1M时考虑可训练参数版本。
swish 激活函数
07-27
Swish（或称为自适应Sigmoid激活函数）是一种用于神经网络的激活函数。Swish函数的数学表达式为f(x) = x * sigmoid(x)，其中sigmoid是Sigmoid函数。Swish激活函数在2017年由Google的研究人员提出，并在一些实验中表现出比ReLU等常用激活函数更好的性能。 Swish激活函数具有一些有趣的性质，例如它是平滑的，并且在x趋近于负无穷时呈现出类似ReLU的线性行为，而在x趋近于正无穷时呈现出类似Sigmoid函数的饱和行为。这种特性可以帮助网络学习更复杂的函数，并且在一些情况下可以提高模型的准确性和收敛速度。 需要注意的是，Swish激活函数在计算上相对于ReLU和Sigmoid函数会更加复杂，因此在一些资源受限的环境中可能不适用。此外，Swish激活函数使用了Sigmoid函数，因此在网络层较深时可能会出现梯度消失的问题，需要注意适当的初始化和正则化方法来缓解这个问题。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值