Probabilistic PCA

前言

一直觉得PCA还是比较简单容易理解的，但是到了Probabilistic PCA（PPCA）就开始觉得复杂起来。PCA出来已经有100年时间，而PPCA到了1999年才出来。这段时间看了这方面的资料，以下将自己的理解记录一下

介绍

假设有数据$X,X\in {\mathbb{R}}^{m\times n}$，且各列已经以0作为均值中心化，且相互独立。第i行表示为第i个观察样本$x_i$,不是变量。未加说明，所有向量为列向量
$$X=[x_1,\cdots ,x_m{]}^T$$
一个潜在变量模型可以表述为下述形式：
$$x=Wz+\mu +ϵ$$
z是潜在变量，W属于潜在因子，和权值矩阵不一样。由于X已经中心化，这里的均值$\mu$可以忽略。给定不同的$ϵ$，这个模型可以衍生出PCA，PPCA，Factor Analysis（FA）。

PCA

最熟悉的PCA目标是如下的形式
$$arg\underset{w}{\max }||Xw|{|}_2^2$$
这个假定有一些粗暴的认定方差最大的方向w，代表了数据X中的大多数信息，在计算上，跟概率没有什么直接的联系。

令 $ϵ\to 0$
$$\begin{gathered} \Rightarrow x=Wz \\ X=[x_1,\cdots ,x_m{]}^T=[W{z}_1,\cdots ,W{z}_m{]}^T=[z_1,\cdots ,z_m{]}^T{W}^T=Z{W}^T \\ \underset{W}{\mathrm{argmax}}\sum _{i=1}^m||z_i-{\mu }_z|{|}_2^2=\sum _{i=1}^m||W^T{x}_i|{|}_2^2=tr(W^T{X}^{T}XW) \end{gathered}$$

PPCA

$$x\sim N(Wz,{\sigma }^{2}I),z\sim N(0,I)$$




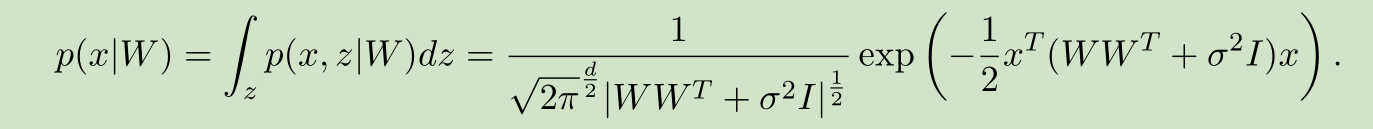
PPCA允许数据中带有的白噪声，一定程度上，能更好的反应真实的数据。但在实际应用中，PPCA似乎并没有比PCA好多少。

Factor Analysis

$$x\sim N(Wz,D),z\sim N(0,I)$$ D是对角阵。FA是没有解析解的，它的因子解析也很随意，带有很大的主观性。

总结

PCA是PPCA的特殊形式，而PPCA又是FA的特殊形式

参考文献

1. Michael E. Tipping, Christopher M. Bishop. Probabilistic Principal Component Analysis[J]. Journal of the Royal Statistical Society, 1999, 61(3):611-622.
2. https://www.cs.ubc.ca/~schmidtm/Courses/540-W16/L12.pdf
   这个课程感觉相当棒，推荐一下