word2vec学习笔记之CBOW和skip-gram

在上一篇学习笔记《 word2vec学习笔记之文本向量化概述》中介绍了word2vec提出的一些背景（当然，除了该篇文章中所说的一些向量化方法之外，在word2vec之后，还有fasttext，glove等其他方法，但在 word2vec学习笔记系列中不对这些新的方法进行介绍）。本文将详细针对word2vec中的CBOW和skip-gram这两种形式进行详细介绍。本文主要是学习《word2vec Parameter Learning Explained》进行笔记。
word2vec的两个模型与 上一篇笔记中提到的NNLM相似，均是在训练语言模型的过程中，使用语言模型的中间产物来得到词表的词向量。

1. Continuous Bag-of-Word Model(CBOW)

上图是连续词袋模型CBOW的结构图。该模型中，是使用上下文词汇来预测中间词。下面将与《word2vec Parameter Learning Explained》相同，分别从一个词的上下文和多个词的上下文来进行介绍。

1.1 One-word context（一个词的上下文）

这里是先简单的从一个词的输入上下文开始介绍，即假设输入侧只有一个词。此时CBOW模型的结构如下

上图中，输入层是一个词的one-hot形式，假设词表大小为V，那么输入是一个大小为V维的one-hot向量，该one-hot向量中，仅有所对应的词的下标处为1，其他位置均为0，我们可以将输入向量记为$x$。
输入层经过与一个$V\ast N$大小的矩阵$W_{V\ast N}$相乘后，得到N维大小的隐藏层的向量$h$，从输入层到隐藏层可以理解为是一个全连接过程，但是跟平时的全连接不同的是，这里没有进行非线性函数的处理。并且，由于输入是一个one-hot向量，因此相乘后的结果实际上是从矩阵$W_{V\ast N}$中取出第$k$行的向量（one-hot向量中1的下标为k），也就是词$w_I$所对应的词向量。即$$h=W^{T}x=W_{k,\cdot }^T:=v_{w_I}^T$$
隐藏层再经过与一个$N\ast V$大小的矩阵$W^{\prime }$相乘后，得到V维大小的输出层的向量$u$。其中输出层向量中的第$j$个元素$u_j$就是矩阵$W^{\prime }$中的第$j$列向量$v_{w_j}^{\prime }$与隐藏层向量$h$的乘积$$u=h{W}^{\prime }$$$$u_j={v_{w_j}^{\prime }}^{T}h$$然后将输出的向量$u$进行softmax处理，得到此表中每一个词的预测概率，而输出概率最大的词即为本次预测的结果。即，输入$w_I$输出$w_j$的概率为$$p(w_j|w_I)=y_j=\frac{exp(u_j)}{{\sum }_{j^{\prime }=1}^{V}exp(u_{j^{\prime }})}$$
隐藏层到输出层之间的权重更新
在模型训练过程中，假设当输入的词是$w_I$时，期望输出的词是$w_O$，那么我们希望$p(w_O|w_I)$能够最大，即我们训练的目标是使得下面的式子最大化$$\max p(w_O|w_I)=\max y_{j\ast }=\max \log y_{j\ast }=u_{j\ast }-\log \sum _{j^{\prime }=1}^{V}exp(u_{j^{\prime }}):=-E$$其中，$E=-\log p(w_O|w_I)$就是我们所期望能够达到最小的损失函数，$j\ast$就是实际输出词或者说是我们期望输出词在此表中的下标。
接下来，我们使用反向传播来进行权重的更新。首先是求损失函数$E$对于$u_j和w_{ij}^{\prime }$的求导（$u_j$是输出层输出向量的第$j$个值，$w_{ij}^{\prime }$是矩阵$W^{\prime }$的第$i$行第$j$列的元素）$$\frac{\partial E}{\partial u_j}=y_j-t_j:=e_j$$$$\frac{\partial E}{\partial w_{ij}^{\prime }}=\frac{\partial E}{\partial u_j}\cdot \frac{\partial u_j}{\partial w_{ij}^{\prime }}=e_j\cdot h_i$$其中，当$j=j^{\ast }$的时候$t_j$为1，否则为0。于是，矩阵$W^{\prime }$的更新公式如下$${w_{ij}^{\prime }}^{(new)}={w_{ij}^{\prime }}^{(old)}-\eta \cdot e_j\cdot h_i$$或者$${v_{w_j}^{\prime }}^{(new)}={v_{w_j}^{\prime }}^{(old)}-\eta \cdot e_j\cdot h$$其中$\eta$是learning rate。

输入层到隐藏层之间的权重更新
与上述”隐藏层到输出层之间的权重更新“过程类似，可以使用以下几个式子求得损失函数$E$对$h_i和w_{ki}$的求导$$\frac{\partial E}{\partial h_j}=\sum _{j=1}^V\frac{\partial E}{\partial u_j}\cdot \frac{\partial u_j}{\partial h_i}=\sum _{j=1}^V{e}_j\cdot w_{ij}^{\prime }:=E{H}_i$$$$\frac{\partial E}{\partial w_{ki}}=\frac{\partial E}{\partial h_i}\cdot \frac{\partial h_i}{\partial w_{ki}}=E{H}_i\cdot x_k$$其中$$h_i=\sum _{k=1}^V{x}_k\cdot w_{ki}$$而由于输入向量$x$中仅有一个元素非零，因此$${v_{w_I}}^{(new)}={v_{w_I}}^{(old)}-\eta E{H}^T$$

1.2 Multi-word context(多个词的上下文)

多个词上下问的CBOW的结构图如下

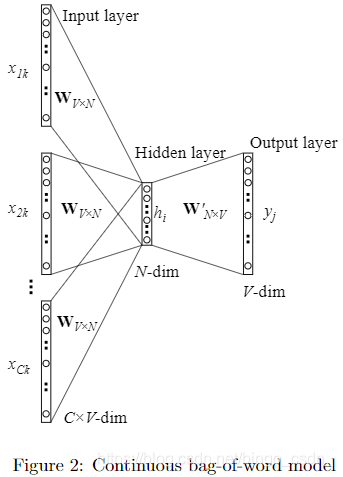
多个词的上下文与单个词的上下文的主要区别在于，每次训练的时候，输入层中的输入词不是一个而是多个。于是，从输入层到中间层的映射变为，将每一个单独的输入词所对应的向量做均值$$h=\frac{1}{C}{W}^T(x_1+x_2+...+x_C)=\frac{1}{C}(v_{w_1}+v_{w_1}+...+v_{w_C}{)}^T$$其中，C是输入层输入词的个数。于是损失函数也就变为$$E=-\log p(w_O|w_{I,1},\cdot \cdot \cdot ，w_{I,C})$$$$=-u_{j^{\ast }}+\log \sum _{j^{\prime }=1}^{V}exp(u_{j^{\prime }})$$$$=-{v_{w_O}^{\prime }}^T\cdot h+\log \sum _{j^{\prime }=1}^{V}exp({v_{w_j}^{\prime }}^T\cdot h)$$于是，更新$W^{\prime }和W$中的值的公式为$${v_{w_j}^{\prime }}^{(new)}={v_{w_j}^{\prime }}^{(old)}-\eta \cdot e_j\cdot h$$$${v_{w_{I,c}}^{\prime }}^{(new)}={v_{w_{I,c}}^{\prime }}^{(old)}-\frac{1}{C}\cdot \eta \cdot E{H}^T$$

2. Skip-gram model

上图是跳字模型skip-gram的结构图。该模型中，是使用中间词来预测上下文词汇。
下图中每一个节点均是表示一个向量，将上图中的每一个节点展开为向量，就与下面的图相同

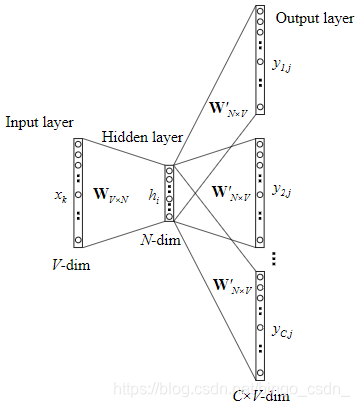
在skip-gram中的输入层到中间层的过程，就与1.1节中介绍的相似，于是也就有了$$h=W_{(k,\cdot )}^T:=v_{w_I}^T$$在隐藏层到输出层中，是有多个词输出，而每一个词的输出概率同样是$$p(w_{c,j}=w_{O,c}|w_I)=y_{c,j}=\frac{exp(u_{c,j})}{{\sum }_{j^{\prime }=1}^{V}exp(u_{j^{\prime }})}$$于是skip-gram的损失函数就是$$E=-\log p(w_{O,1},w_{O,2},...,w_{O,c}|w_I)$$$$=-\log \prod _{c=1}^C\frac{exp(u_{c,j_c^{\ast }})}{{\sum }_{j^{\prime }=1}^{V}exp(u_{j^{\prime }})}$$$$=-\sum _{c=1}^C{u}_{j_c^{\ast }}+C\log \sum _{j^{\prime }=1}^{V}exp(u_{j^{\prime }})$$其中$w_I$是输入的词，w_{O,c}表示输入的C个词中的第c个。于是，损失函数对输出的第c个输出词向量的第j个元素的求导为$$\frac{\partial E}{\partial u_{c,j}}=y_{c,j}-t_{c,j}:=e_{c,j}$$损失函数E对矩阵$W^{\prime }$中的第i行第j列元素的求导为$$\frac{\partial E}{\partial w_{ij}^{\prime }}=\sum _{c=1}^C\frac{\partial E}{\partial u_{c,j}}\cdot \frac{\partial u_{c,j}}{\partial w_{ij}^{\prime }}=E{I}_j\cdot h_i$$于是，可更新权重$${w_{ij}^{\prime }}^{(new)}={w_{ij}^{\prime }}^{(old)}-\eta \cdot E{I}_j\cdot h_i$$或者$${v_{w_j}^{\prime }}^{(new)}={v_{w_j}^{\prime }}^{(old)}-\eta \cdot E{I}_j\cdot h$$
而在skip-gram的输入层到隐藏层的过程与一个词上下文的CBOW相似，矩阵$W$的更新公式为$$v_{w_I}^{(new)}=v_{w_I}^{(old)}-\eta \cdot E{H}^T$$