本文介绍了如何通过留数计算确定有理真分式部分分式的待定系数。在Q(x)的根为单根或重根的情况下，利用留数公式可以求解这些系数。这一方法不仅适用于实数根，也适用于复数根。通过将函数视为复变函数并应用复变函数的积分和留数理论，可以有效地将有理真分式化为部分分式和形式。
确定部分分式中待定系数的留数方法
在将有理真分式化为确定部分分式和的过程中，可以使用留数对部分分式的系数进行求解。
这里介绍一篇论文，证明可以在论文中查看
注：链接已经失效，请大家自行到知网进行检索
设有理真分式
f
(
x
)
=
P
m
(
x
)
Q
n
(
x
)
f(x)=\frac{P_m(x)}{Q_n(x)}
f(x)=Qn(x)Pm(x)
其中，
m
<
n
m\lt n
m<n
分为以下两种 情况进行讨论
a. Q(x)=0的根均为单根
.
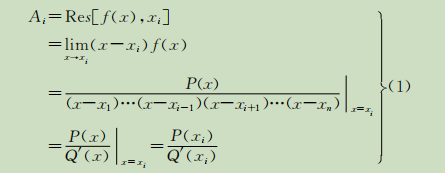
即，此时要确定的系数就是f（x）在对应极点上的留数
b.根中有重根
单根的确定方法同a情况中的确定方法，对于重根,设x1 为r重根,考虑Bk
B
k
=
R
e
s
[
(
x
−
x
1
)
k
−
1
f
(
x
)
,
x
1
]
此时
x
1
为
(
x
−
x
1
)
k
−
1
f
(
x
)
的
r
−
(
k
−
1
)
=
r
−
k
+
1
级极点
B_k=Res[(x-x_1)^{k-1}f(x),x_1 ] \\ 此时x_1为(x-x_1)^{k-1}f(x)的r-(k-1)=r-k+1级极点
Bk=Res[(x−x1)k−1f(x),x1]此时x1为(x−x1)k−1f(x)的r−(k−1)=r−k+1级极点
利用留数极点计算公式 得，
B
k
=
1
(
r
−
k
)
!
lim
x
→
x
1
[
(
x
−
x
1
)
r
f
(
x
)
]
(
r
−
k
)
=
1
(
r
−
k
)
!
[
(
x
−
x
1
)
r
f
(
x
)
]
(
r
−
k
)
∣
x
=
x
1
B_k=\frac{1}{(r-k)!}\lim_{x \to x_1} [(x-x_1)^{r}f(x)]^{(r-k)} \\{\color{Blue}=\frac{1}{(r-k)!}[(x-x_1)^rf(x)]^{(r-k)}|_{x=x_1} }
Bk=(r−k)!1x→x1lim[(x−x1)rf(x)](r−k)=(r−k)!1[(x−x1)rf(x)](r−k)∣x=x1
注：上述结论虽然是在实根条件下得出的，但经过博主研究，上述结论在根为复数单根，以及复数重根的条件下同样成立。
c.总结——基本思想
要将有理真分式 f ( x ) = P m ( x ) Q n ( x ) 在实数范围内化为部分分式和的形式，可将ｆ ( x ) 视为特殊的复变函数ｆ ( z ) 先将ｆ ( z ) 化为部分分式和的形式 , 根据复变函数的积分和留数理论可得 其待定系数为ｆ ( z ) 在极点处的留数 要将有理真分式\\ f(x)=\frac{P_m(x)}{Q_n(x)} \\在实数范围内化为部分分式和的形式，可将ｆ(x)视为特殊的复变函数ｆ(z) \\先将ｆ(z)化为部分分式和的形式,根据复变函数的积分和留数理论可得 \\其待定系数为ｆ(z)在极点处的留数 要将有理真分式f(x)=Qn(x)Pm(x)在实数范围内化为部分分式和的形式，可将ｆ(x)视为特殊的复变函数ｆ(z)先将ｆ(z)化为部分分式和的形式,根据复变函数的积分和留数理论可得其待定系数为ｆ(z)在极点处的留数
扫一扫
4217
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
