
多相插值滤波器将一组 N 个原滤波器系数 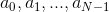 ,映射为P个多相子滤波器
,映射为P个多相子滤波器 , 转换公式与式3-1相同:
, 转换公式与式3-1相同:
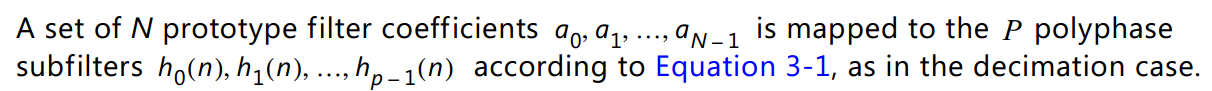

每个新的输入采样x(n)同时并行送入P个多相子滤波器,同时得到P个输出采样,每个多相子滤波器输出一个采样送到滤波器输出端口,输出端口从第一个多相子滤波器开始依次选择多相子滤波器的输出。由于输入采样是同时并行送入每个多相子滤波器的,因此多相插值滤波器的输出采样速率是输入数据采样速率的P倍。
(a) 利用对称性实现多相插值器

下面用例子说明:
假设在一个抽头数为15的滤波器,滤波器系数如下,对该滤波器进行3倍插值,得到3个子滤波器,系数分别为:


可见,第一个和第三个子滤波器是不对称的,应用对称性技术,经过简单的加法和减法运算对两个滤波器系数进行处理得到;
(2) 系数填充
关于系数填充的话题在之前提到过,那是对于使用MAC设计对称系数滤波器时提出的一种优化方案;
在对称滤波器基础上进行插值,如果速率和滤波器抽头数的组合导致子滤波器的系数个数不匹配,则滤波器系数的重新组织将可能使滤波器的相位响应发生变化,即结果得到的冲激响应移位了若干个输出采样。
例如:对抽头数为14的滤波器进行4倍插值,则需要有16个抽头才合理,这样的话,我们就需要在系数矢量的前面补充一个零,在系数矢量的后面也补充一个零系数,从而保证子滤波器系数的对称性,但结果是滤波器的相位响应发生了变化。避免出现相位响应变化的方法是要么强制滤波器以非对称的结构实现,要么用能支持所选实现结构的额外系数来实现。下面给出了一些扩展到较大滤波器的例子: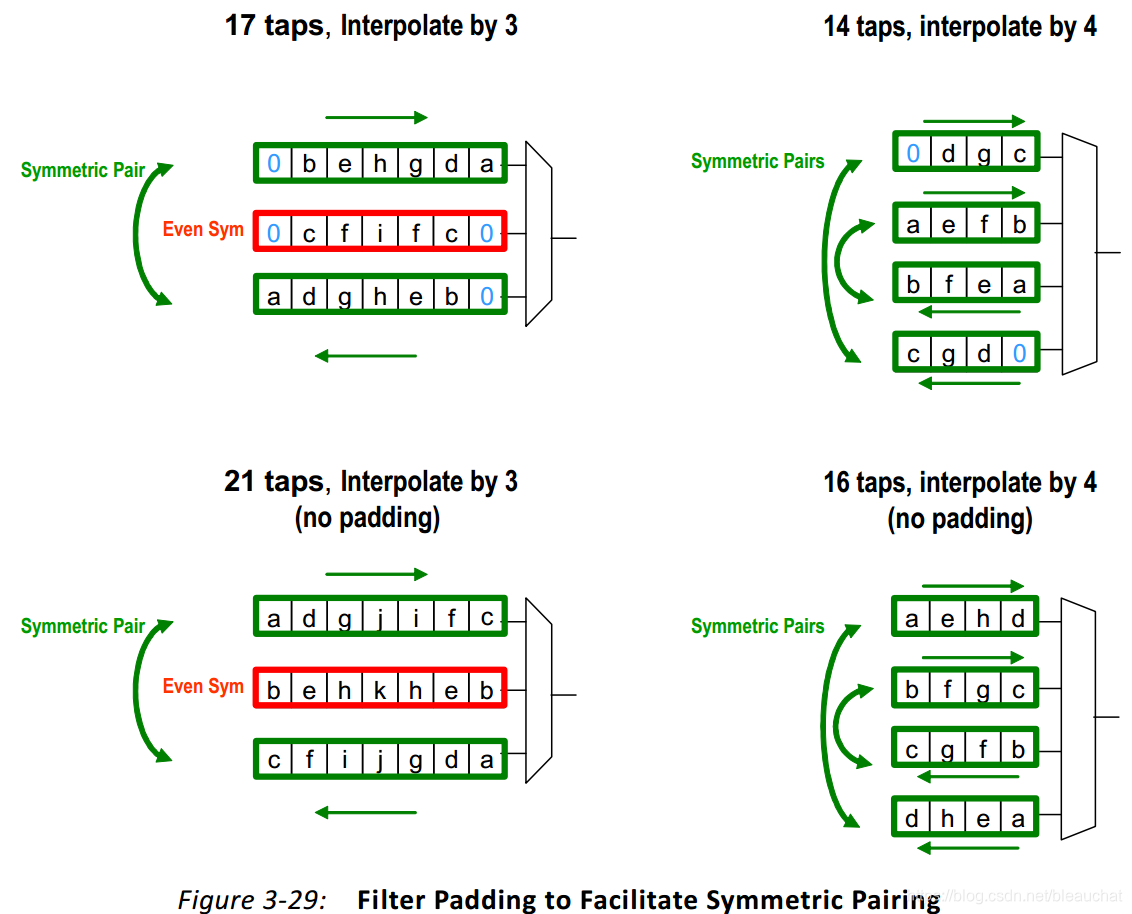
























 2016
2016

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








