Introduction

什么是静态时序分析？

在介绍什么是STA之前，我们需要了解为什么需要进行时序分析：

（1）时序约束 timing constraint 

 验证我们的设计是否达到了时序要求，也就是验证设计是否达到了我们所需要的时钟频率；通常我们会在限定的芯片速度、面积和功耗之间做出取舍，但是芯片必须满足时序约束以在所需的时钟频率工作，所以时序约束是最重要的约束.

（2）操作环境

我们应该确保芯片在任何操作环境下都能正常的工作，这里的操作环境是指添加其他组件的情况.

（3）器件选型

比如我们要为一款微处理器选择一个存储设备：如果存储器的速度太慢则不符合要求，如果速度太快价格又太贵。因此我们要选择一款与微处理器速度匹配的存储器.

所以，时序分析至关重要以确保我们的设计达到了我们时序约束的要求，这意味着设计要尽可能的满足建立时间和保持时间以及脉宽的要求.因此时序分析是IC设计中不可或缺的重要环节！

时序分析的类型

（1） 静态时序分析（STA）

在没有输入和输出的情况下检查静态延时需求；STA不依赖输入向量，通过分析电路拓扑并计算不同信号达到各点的时间窗口，将其与要求信号达到该点的时间进行比较来验证是否满足时序；和动态时序分析相比，它不需要输入激励，因此速度会很快，并且它是Path Based分析，采用穷举型逻辑，如下图所示，理论上能分析到所有同步逻辑是否违反约束：

那么如何去做STA，需要准备些什么文件呢？简单的可以用下图表示：

我们需要准备设计的libarary data (包括cell的lib和operating condition等等)，Timing constraints(包括clock的描述，design boundry的约束等其他sdc)，Gate-level-netlist，sdf/spef等rc信息文件； 然后需要指定时序分析模式，最后会产生设计中的详细时序分析报告. 

常用的静态时序工具是SYNOPSYS公司的PrimeTime.

（2）动态时序分析

通过对设计添加激励来检查输出是否正确来验证是否满足时序要求；通过输入向量作为激励，来验证整个设计的时序功能，动态时序分析的精确与否取决于输入激励的覆盖率，它最大的缺点就是速度非常慢，通常百万门的设计想全部覆盖测试的话，时间就是按月来计算了；

时序分析的基础

时序分析的基础就是"clock"和"sequential component"（FF和latch）。下面列举了关于时钟和FF我们通常要注意的事项：

（1）关于时钟

• 必须有很高的质量，即无毛刺；
• 必须保证任何生成时钟都是干净的，具有有界的周期和占空比，并且已知和源时钟之间的相位关系；
• 时钟不管在high还是low相位的情况下都必须满足最小脉宽的要求；
• 对于特定的电路，如PLL，也许会存在最小时钟抖动（clock jitter）的要求.因为随着时钟频率的增加，时钟抖动会变大；
• 当要把一个时钟边界的数据传递到另一个时钟域时要确保在最坏的情况下的占空比被用于计算延时，一个常见的错误就是假设每个时钟都是50%的占空比； 

 （2）关于FF和latch

• 必须确保FF的所有参数都满足，唯一的例外是当同步器用于同步异步信号的时候；
• 对于异步预置和清零，Recovery和Removal（恢复和删除）两个参数必须满足；
• 对于最早或最晚的时钟到达时间都应该满足建立时间和保持时间要求；
• 建立时间通常由设计者计算，而保持时间一般不计算；
• 在进行跨时钟域处理时，必须确保两个时钟之间的相位关系满足建立保持时间或者两个时钟域之间已经正确同步；

静态时序分析STA

STA通过检查在最糟糕的情况下所有可能发生时序违例路径来分析设计的时序性能，它考虑的是每个逻辑单元的最差延时情况而不是电路的逻辑操作.

相比于电路仿真，STA的优点有：

（1）速度更快，因为STA不需要遍历所有可能的激励；

（2）更彻底完整，因为它检查了所有逻辑单元最差的时序情况，而不仅仅是被特定激励触发的那部分；

需要强调的是，STA只检查是否满足时序要求，而不会检查逻辑功能！STA努力回答的问题是:"在所有可能的情况下当时钟到达时数据是否会准确的出现在每个同步单元的数据输入口？"还有一点，STA只适合用来分析同步逻辑电路！

STA主要分为以下3步：

（1）将设计拆分成多组时序路径；

（2）计算每条路径上的传输延时；

（3）检查设计内部和输入输出端口的违反时序约束的情况；

STA工具分析从每个起点到每个终点的所有路径的延时情况，并将它与该路径的约束所需求的时间进行对比，因此所有的路径都需要约束，约束一般是通过定义时钟来完成，以及电路的最开始输入和最终输出的约束.

在我们开始学些STA之前，我们需要了解一些STA的术语：timing path（时序路径）、arrive time、required time 、slack和critical path。下面我们将一一讲述：

timing path

STA会分析以下四种路径：

• data path 数据路径
• clock path 时钟路径
• clock gating path 时钟门控路径
• asynchronous path 异步路径

每一条timing path都有一个起点和一个终点，起始点和终点的定义对于不同的路径来说各不相同，例如对于data path，起点是数据在时钟沿发送的位置，数据经过组合逻辑，然后被另一个时钟沿捕获。正是由于不同路径的起始点不同，所以对这点了解清楚对于我们阅读时序分析报告和纠正时序违例很重要.

（1）data path

起点可以是设计的输入端口（因为输入数据可以是从外部源发送过来的）或者FF的时钟端口；

终点可以是FF的数据输入端口或者设计的输出端口（因为数据可以被外部设备捕获） ；

（2）clock path

起点是时钟输入端口，终点是FF的时钟管脚；

（3）clock gating path

起点是设计的输入端口，终点是时钟门控单元的输入端口；

（4）asynchronous path

起点是设计的输入端，终点是FF的复位、置位或清零端；

data path 数据路径

如果我们使用两种起点和终点的组合，那么就存在四种类型 的时序路径，分别是：

• input port/pin to register data pin  输入端口到寄存器的数据输入端口
• input port/pin to output port/pin 输入端口到输出端口
• FF clock pin/port to register data pin FF的时钟输入端口到FF的数据输入端口
• FF clock pin/port to output port/pin FF的时钟输入端口到输出端口

上面这张图展示了四种时序路径.

 clock path 时钟路径

看下图：

时钟从设计的输入端口作为起点，终点是FF的时钟端口，起始点之间可能包括大量的buffer、反相器或者时钟分频器.

clock gating path 时钟门控路径

时钟可以通过一个门控单元来获得更佳的时钟特性，在这种情况下时钟特性会发生改变，我们通常将这种加上门控单元的路径称为时钟门控路径。看下图：

LD引脚不存在任何时钟，但是它用于选通原始的clk信号，输出作为新的时钟进入FF。对于这类路径既不属于时钟路径也不属于数据路径，所以取名叫时钟门控路径.

asynchronous path 异步路径

 

如上图，一条路径的起点是输入端口，终点是FF的异步置位或清零端，这种路径叫做异步路径.置位/复位是独立于时钟边沿的，可以再任何时间进行，因此可以说这种路径不同于同步电路的其他路径，我们称之为异步路径.

其他路径类型：

• critical path 关键路径
• false path 伪路径
• multi-cycle path  多周期路径
• single-cycle path 单周期路径
• launch path 发送路径
• capture path 捕获路径
• longest path 最长路径（也叫作最差路径或最大延时路径）
• shortest path 最短路径（也叫作最佳路径或最小延时路径）

critical path 关键路径 

简而言之，可以说最差路径（longest path）就是关键路径.

• 关键路径是时钟敏感的路径，因为不允许再添加额外的逻辑门到这些路径中，否则会增加额外的时钟延时；
• 关键路径也指那些不满足时序约束的路径.通常在你综合完成后，仿真工具会给出那些具有最大negetive slack的路径，此时你要确保这些路径不是伪路径或者多周期路径。因为如果是这两种路径的话，就可以忽略这些路径了. 

举一个简单的例子：STA工具会在FF的Q端到下一个FF的D端路径上添加延时，再比较这个延时加上建立时间以及时钟偏斜的和与时钟周期的关系。如果加起来的延时小于时钟周期，则满足时序约束；如果大于，则发生时序违例。而关键路径就是这些违例路径当中延时超过时钟周期最多的一个或者在所有路径都满足约束的条件下，延时最接近时钟周期的一条路径.

false path 伪路径

物理上存在，但是在逻辑功能上不正确的路径，也就是没有数据从该路径的起点发送到路径的终点，这种路径叫做伪路径。伪路径在设计中存在的原因可能有几个。

有些时候我们必须明确定义和创建设计中的一些伪路径，如两个异步时钟之间的关联路径。

STA将伪路径排除在外，在伪路径上不会做时序分析。

由于伪路径不存在数据发送，所以它们通常不满足时序约束。在时序收敛的时候考虑伪路径会导致时序违例，而修复伪路径的操作将会给设计带来不必要的复杂度。

在你的设计中，也许存在少数路径它们既不是关键路径，也可能会掩盖其他时序优化的重要路径或者在正常环境中基本上不会出现。这种情况下为了减少运行时间或者优化时序，我们可以将它们声明为伪路径。这样，时序分析工具就会忽略这些路径并且在时序优化的时候也不会聚焦于这些路径上。如下图，存在于两个选择端连在一起的MUX，某些路径根本就不可能会发生，这些路径就是伪路径。

我们可以看到伪路径1和2不可能同时发生，但是在做时序优化的时候它们可以影响另一条路径的时序。这种情况，我们应该将其中的一条定义为伪路径.一般情况下，伪路径存在于：

• 芯片的异步输入端口；
• 测试输入端口，这些端口仅用于测试，在芯片正常工作时为禁止状态；
• 配置输入端口；

 multi-cycle path  多周期路径

 从起点到终点所需的时间超过一个周期的路径，因此多周期路径允许多个周期的传输延时。通过定义多周期路径约束去告诉时序分析工具该路径需要N个周期来完成，所以此时的定时检查变为该路径延时必须小于N*period，N>1.

举个例子来说明：

当你在做两个时钟的交叉，从一个30MHz的时钟到60MHz的时钟，两个时钟同源同相；通常的约束是从30M时钟的上升沿到60M时钟的最近上升沿，两者之间周期相差16ns。如果此时你有一个信号从60时钟域传送到30时钟域，此时你可以允许该信号的传送周期为32ns，即2个60MHz时钟的周期。

single-cycle path 单周期路径

 从路径的起点到终点只需要一个时钟周期的路径，默认的路径都为单周期路径；

launch path 发送路径和capture path 捕获路径

 

上图中，FF1为发送寄存器，FF3为捕获寄存器.发送路径指的是发送时钟的路径，负责在发送寄存器处发送数据；捕获路径指的是捕获时钟的路径，负责在接收寄存器处接收数据。看下图：

上面数据路径的起点是FF0的时钟端，终点是FF1的D端口；launch clock path和data path共同构成了数据到达时间；捕获时钟周期和时钟路径延时构成了数据要求到达时间；

longest path 最长路径和 shortest path 最短路径

 

timing borrowing

 timing borrowing是指长延时路径从后续的短延时路径借用时间的技术。看下图：

各个锁存器之间的延时如上所示，中间的G1、G2、G3、G4为组合逻辑。如果假设上面的设计采用触发器，则时钟周期至少是8ns才不会发生违例。现在假设锁存器都是透明的，对于周期为5ns的时钟，path1可以从path2借用3ns，而path3可以从path4借用1ns，从而使得时序不出现违例的情况。

注意，基于锁存器的设计完成上面设计所需的时间为20ns，而同样的触发器却需要32ns。

我们再看下面一个复杂一点的设计：

对于一个基于锁存器的设计，每一条执行路径的起点都必须是驱动锁存器使能的时刻，终点都是被驱动锁存器使能的时刻。

一些重要的事情：

（1）如果timing borrowing 发生在同一个周期，这意味着发送和捕获锁存器使用同相的时钟；如果两个锁存器所用的时钟不同相，则timing borrowing不会发生，这种情况下timing borrowing被EDA软件禁止。

（2）timing borrowing通常影响建立时间裕量的计算，因为timing borrowing推迟了数据到达时间；由于保持时间裕量一般使用最早的到达时间来计算，所以timing borrowing不会影响。

几个重要的术语：

（1）最长借用时间（maximum borrow time） 脉冲宽度减去锁存器的建立时间

（2）负借时间（negative borrow time） 数据到达时间减去时钟边沿为负数，则说明没有timing borrowing

建立时间与保持时间的基本概念

 接下来我们将回答以下几个问题：

（1）什么是建立时间和保持时间？

（2）建立和保持的定义

（3）建立和保持违例

（4）如何计算一个设计中的建立和保持违例？

什么是建立时间和保持时间？

如上图所示，一个输入口DIN和一个外部时钟CLK通过buffer和组合逻辑同步进入D触发器的D端口和clk端口。现在为了正确捕获数据，数据必须在时钟沿到clk端口时准确的出现在D端口上。这里我们假设FF的建立和保持时间为0.

这里只存在两种情况：

• Tpd DIN>Tpd CLK  这种情况下为了在时钟沿到达管脚C端捕获数据，你必须在时钟沿到达CLK之前保持输入数据稳定Ts=Tpd DIN-Tpd CLK时间，也就是说在时钟到达CLK之前，输入数据在DIN必须保持稳定Ts时间，这就是建立时间.
• Tpd DIN<Tpd CLK 这种情况下为了在时钟到达管脚C时捕获数据，输入数据必须保持稳定Th=Tpd CLK-Tpd DIN时间，也就是说在时钟到达CLK之后，数据在DIN必须保持稳定Th时间，这就是保持时间.

当然以上的两种情况不可能同时存在，所以以上的情况可能是：

例如，对于组合逻辑路径：

data path(最大值，最小值)=（5，4）；

clock path(最大值，最小值)=（4.5，4.1）；

所以建立时间Ts=5-4.1=0.9ns、保持时间=4.5-4=0.5ns.

建立和保持的定义

 

如上图所示：

建立时间就是在时钟沿到来之前数据必须保持不变的最短时间，只有满足了建立时间输入数据才能被可靠的采样；

保持时间就是在时钟沿到来之后数据必须保持不变的最短时间，只有满足了保持时间输出数据才能被可靠的采样；

建立和保持违例

如果数据在tsu之内的时间段内发生变化，则发生建立时间违例；如果数据在thd之内的时间段内发生变化，则发生 保持时间违例；

计算设计中的建立和保持违例

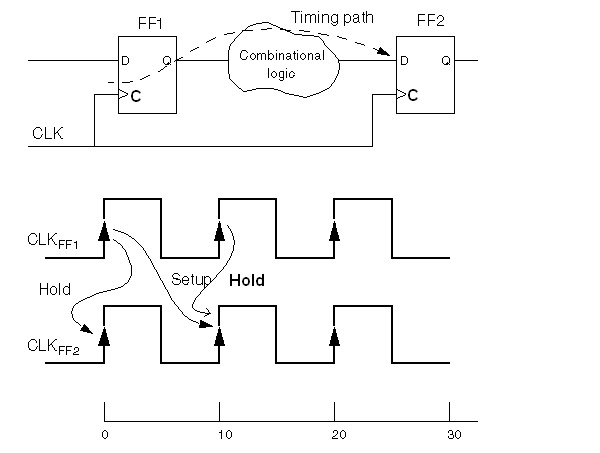
数据路径FF1/C->->FF1/Q->组合逻辑->FF2/D，所以对于单周期路径，假设数据在0ns时发送，则在10ns时被捕获，对应的两个时钟沿分别为发送沿和捕获沿；

对于建立时间分析，0ns为发送沿，10ns为捕获沿，为了满足建立时间，数据必须在10-Ts之前到达FF2/D并且保持稳定（这里的Ts是FF2的），否则将发生建立时间违例；

对于保持时间分析，10ns作为下一个数据发送沿，为了满足保持时间，数据必须在10ns之后保持稳定Th（这里的Th是FF2的），且第二个在FF1发送的数据必须在10+Th之后才能到达FF2/D，否则将发生保持时间违例.

我们用下面的图再来分析建立检查：

数据在FF1/D发送，然后到达FF2/D，中间经过组合逻辑延时.在数据要求时间之前到达了FF2/D，所以不存在建立时间违例，建立时间裕量=data required time - data arrival time。

由下面的图再来分析保持检查：

上图我们可以看到clkB相对于clk发生了延时，这是加入了buffer的原因.由于FF1/Q与FF2/D之间的逻辑延时太短，导致下一个数据很快就传送到FF2/D，上一个数据没有稳定Th的时间就被下一个数据替换（电平发生翻转），所以发生保持时间违例。保持时间违例可以通过减少时钟延时（clk到clkB的延时）或者增加组合逻辑延时来避免！

我们来看下面的例子：

我们要考虑两个路径，数据路径和时钟路径.

数据路径：从时钟的输入端口到FF/D         clk->FF1/clk->FF1/Q->FF2/Q

时钟路径：从时钟的输入端口到FF/CLK    clk->FF2/clk

最大数据路径延时=2+11+2+9+2=26ns  最小路径延时=1+9+1+6+1=18ns

最大时钟路径延时=3+9+3=15ns 最小时钟路径延时=2+5+2=9ns

所以，数据要求到达的最晚时间（经过一个时钟周期）=最小时钟路径延时+T-Tsu=9+15-4=20ns

建立时间裕量=数据要求到达的最晚时间-最大数据路径延时=20-26=-6ns  发生建立时间违例

下一个数据要求到达的最晚时间=最大时钟路径延时+Th=17ns

保持时间裕量=下一个数据到达的最早时间-数据要求达到的最早时间=18-17=1ns 没有发生保持时间违例

从上面我们可以看到，建立检查是在下一个时钟沿（时钟周期）分析的，而保持检查是在当前时钟沿分析的.

我们再来看下面一个例子：

首先计算reg2reg delay （寄存器到寄存器的延时，也就是数据路径延时）:

数据路径：U1/clk->U1/Q->U4->U2/D    5+7=12ns           U1/clk->U1/Q->U4->U2/D     5+8=13ns

时钟路径在两个寄存器之间为0ns的延时，所以数据要求到达的最晚时间=T+0-Tsu   13<T-Tsu   T>16ns

然后计算pin2pin delay（输入管脚到输出管脚的延时）:

pin2pin delay=U7+U5+U6=1+9+6=16ns

最后计算clk2out delay（时钟到输出管脚延时，也就是时钟路径延时）：

clk2out delay=U8+U2+U5+U6=2+5+9+6=22ns

所以最大的时钟频率 max cllock freq=1/max(reg2reg，pin2pin，clk2out)=1/22=45.5MHz

总结上面所述：

（1）建立检查是在下一个时钟沿，保持检查是在当前时钟沿；

（2）建立裕量=数据要求到达时间-数据到达时间   保持裕量=下一个数据到达时间-数据要求到达时间

计算时钟最高频率的方法：

再来看下面一个例子：

数据路径：max delay=2+11+2+9+2=26ns  min delay=1+9+1+6+1=18ns

时钟路径：max delay=3+9+3=15ns  min delay=2+5+2=9ns

保持检查：下一个数据要求到达的最晚时间=15+Th=17ns <18 ns 所以不会发生保持违例

建立检查：数据要求达到的最晚时间=9-4+T>26  所以T>21

时序路径延时的进一步讨论

关于如何计算一条路径的延时，存在两种方法：

（1）计算从路径起点到终点的maxdelay和mindelay；

（2）分别以时钟的上升沿和下降沿来计算延时，延时大的为maxdelay，延时小的为mindelay；

这两种方法都是正确的，我们都要用到.其实路径上的延时主要分为两类：逻辑延时和走线延时.

逻辑延时主要是逻辑器件输入管脚到输出管脚的延时，走线延时主要是导线上的延时； 

两种延时与以下的多种因素相关：

我们看下面一个例子：

从UFF1到UFF3存在两条路径，下面我们我们根据提供的信息来分别计算两条路径的延时.

正如上面所计算的那样，STA工具或许会使用类似的方法计算maxdelay和mindelay.

解决建立和保持违例

 

我们来看第一个例子：

数据路径：0.5ns

时钟路径：0ns

建立检查：0.5<0+T-Tsu  =8 没有违例

保持检查：0.5>0+Th=1 发生保持违例

要通过增加组合逻辑延时来解决保持违例，但是组合逻辑延时不能随便添加，要满足建立和保持时间，即：

1<0.5+Tl<8，所以增加的延时     0.5<Tl<7.5