微积分2-常见函数的导数

同步于Buracag的博客;音尘杂记

在微积分1中已经附上了一个常见函数形式的导数，下文主要是关于向量函数及其导数，以及在机器学习和神经网络中常见的Logistic函数、Softmax函数的导数形式。

1. 向量函数及其导数

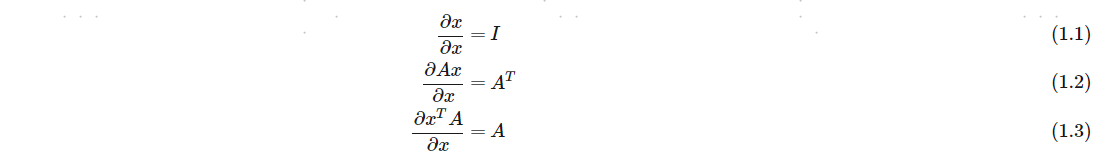
2. 按位计算的向量函数及其导数

假设一个函数$f(x)$的输入是标量$x$。对于一组$K$个标量$x_1,...,x_K$，我们可以通过$f(x)$得到另外一组$K$个标量$z_1,...,z_K$，
$$z_k=f(x_k),\forall k=1,...,K\text{\hspace{1em}(1.4)}$$
为了简便起见，我们定义$x=[x_1,...,x_K{]}^T，z=[z_1,...,z_K{]}^T$，
$$z=f(x)\text{\hspace{1em}(1.5)}$$
其中$f(x)$是按位运算的，即$[f(x){]}_i=f(x_i)$。

当$x$为标量时，$f(x)$的导数记为$f\prime (x)$。当输入为$K$维向量$x=[x_1,...,x_K{]}^T$时，其导数为一个对角矩阵。

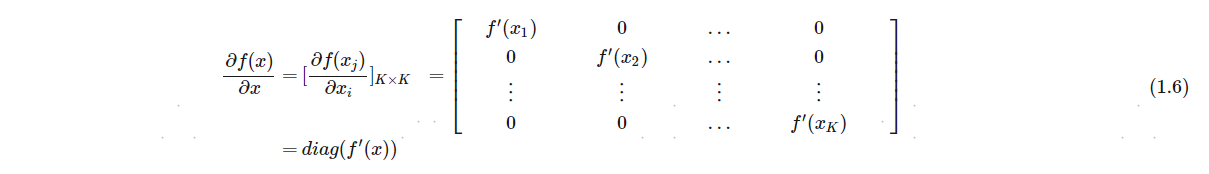
3. Logistic函数的导数

关于logistic函数其实在博文’Logistic loss函数’中已经有所介绍，接下来要说是更广义的logistic函数的定义：
$$logistic(x)=\frac{L}{1+exp(-k(x-x_0))}\text{\hspace{1em}(1.7)}$$
其中，$x_0$是中心点，$L$是最大值，$k$是曲线的倾斜度。下图给出了几种不同参数的Logistic函数曲线。当$x$趋向于$-\infty$时，logistic(x)接近于0；当$x$趋向于$+\infty$时，logistic(x) 接近于$L$。

当参数为($k=1,x_0=0,L=1$) 时，Logistic 函数称为标准Logistic 函数，记为f(x)。
$$f(x)=\frac{1}{1+exp(-x)}\text{\hspace{1em}(1.8)}$$
标准logistic函数有两个重要的性质如下：

当输入为$K$维向量$x=[x_1,...,x_K{]}^T$时，其导数为：
$$f^{\prime }(x)=diag(f(x)\odot (1-f(x)))\text{\hspace{1em}(1.11)}$$

4. Softmax函数的导数

Softmax函数是将多个标量映射为一个概率分布。对于$K$个标量$x_1,...,x_K$，softmax 函数定义为
$$z_k=softmax(x_k)=\frac{exp(x_k)}{{\sum }_{i=1}^{K}exp(x_i)}\text{\hspace{1em}(1.12)}$$
这样，我们可以将$K$个变量$x_1,...,x_K$转换为一个分布：$z_1,...,z_K$，满足
$$z_k\in [0,1],\forall k,\sum _{k=1}^K{z}_k=1\text{\hspace{1em}(1.13)}$$
当Softmax函数的输入为$K$维向量$x$时，

其中$1_K=[1,...,1{]}_{K\times 1}$是$K$维的全1向量。

Softmax函数的导数为

其中式(1.16)请参考 ‘微积分1-导数’ 式(1.13)。

主要参考https://github.com/nndl/nndl.github.io