​多任务学习漫谈：行梯度之事

©PaperWeekly 原创 · 作者 | 苏剑林

单位 | 追一科技

研究方向 | NLP、神经网络

在《多任务学习漫谈：以损失之名》中，我们从损失函数的角度初步探讨了多任务学习问题，最终发现如果想要结果同时具有缩放不变性和平移不变性，那么用梯度的模长倒数作为任务的权重是一个比较简单的选择。我们继而分析了，该设计等价于将每个任务的梯度单独进行归一化后再相加，这意味着多任务的“战场”从损失函数转移到了梯度之上：看似在设计损失函数，实则在设计更好的梯度，所谓“以损失之名，行梯度之事”。

那么，更好的梯度有什么标准呢？如何设计出更好的梯度呢？本文我们就从梯度的视角来理解多任务学习，试图直接从设计梯度的思路出发构建多任务学习算法。

整体思路

我们知道，对于单任务学习，常用的优化方法就是梯度下降，那么它是怎么推导的呢？同样的思路能不能直接用于多任务学习呢？这便是这一节要回答的问题。

下降方向

其实第一个问题，我们在《从动力学角度看优化算法（三）：一个更整体的视角》就回答过。假设损失函数为 ，当前参数为 ，我们希望设计一个参数增量 ，它使得损失函数更小，即 。为此，我们考虑一阶展开：

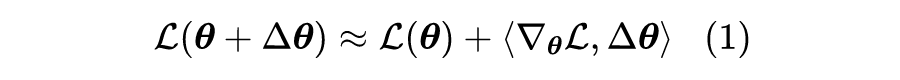
假设这个近似的精度已经足够，那么 意味着 ，即更新量与梯度的夹角至少大于 90 度，而其中最自然的选择就是

这便是梯度下降，即更新量取梯度的反方向，其中 即为学习率。

无一例外

回到多任务学习上，如果假设每个任务都同等重要，那么我们可以将这个假设理解为每一步更新的时候 都下降或保持不变。如果参数到达 后，不管再怎么变化，都会导致某个 上升，那么就说 是帕累托最优解（Pareto Optimality）。说白了，帕累托最优意味着我们不能通过牺牲某个任务来换取另一个任务的提升，意味着任务之间没有相互“内卷”。

假设近似（1）依然成立，那么寻找帕累托最优意味着我们要寻找 满足

注意到它存在平凡解 ，所以上述不等式组的可行域肯定非空，我们主要关心可行域中是否存在非零解：如果有，则找出来作为更新方向；如果没有，则有可能已经达到了帕累托最优（必要不充分），我们称此时的状态为帕累托稳定点（Pareto Stationary）。

求解算法

方便起见，我们记 ，我们寻求一个向量 ，使得对所有的 都满足 ，那么我们就可以像单任务梯度下降那样取 作为更新量。如果任务数只有两个，可以验证 自动满足 和 ÿ