如何度量数据的稀疏程度？

©PaperWeekly 原创 · 作者 | 苏剑林

单位 | 追一科技

研究方向 | NLP、神经网络

在机器学习中，我们经常会谈到稀疏性，比如我们经常说注意力矩阵通常是很稀疏的。然而，不知道大家发现没有，我们似乎从没有给出过度量稀疏程度的标准方法。也就是说，以往我们关于稀疏性的讨论，仅仅是直观层面的感觉，并没有过定量分析。那么问题来了，稀疏性的度量有标准方法了吗？

经过搜索，笔者发现确实是有一些可用的指标，比如 、熵等，但由于关注视角的不同，在稀疏性度量方面并没有标准答案。本文简单记录一下笔者的结果。

基本结果

狭义上来讲，“稀疏”就是指数据中有大量的零，所以最简单的稀疏性指标就是统计零的比例。但如果仅仅是这样的话，注意力矩阵就谈不上稀疏了，因为softmax出来的结果一定是正数。所以，有必要推广稀疏的概念。一个朴素的想法是统计绝对值不超过 的元素比例，但这个 怎么确定呢？

1 相比于 0.0001 很大，但是相比 10000 又很小，所以大和小的概念不是绝对的。直观来想，稀疏的向量存在很多接近于零的数，那么它的绝对值的平均肯定会比较小，又因为大和小的概念是相对的，我们不妨将这个平均值跟最大值做除法，以获得相对结果，所以一个看上去比较合理的指标是

其中 是需要评估稀疏性的向量（下面都假设 并非全等向量，即至少有两个不同的元素），指标越小的向量越稀疏。不过，尽管这个指标有一定的合理性，但它却不够“光滑”，主要是 这个操作极易受到异常值的影响，不能很好地反应数据统计特性。

光滑齐次

于是，我们按照《寻求一个光滑的最大值函数》[1] 的思路，将 换成它的光滑近似。 标准的光滑近似是 ：

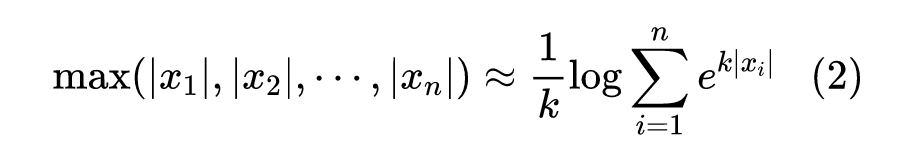
然而，如果这里用 替代 ，并不能起到较好的改进效果。一是因为有 的放大作用， 同样容易受到异常值的影响，二是因为 没有正齐次性，反而不美（所有 乘以正数 ，稀疏性应该不改变）。在《寻求一个光滑的最大值函数》[1] 中我们也给出了一个 的具备正齐次性的光滑近似，它正好是 范数（）：