梯度流（Gradient Flow）：探索通往最小值之路

©PaperWeekly 原创 · 作者 | 苏剑林

单位 | 追一科技

研究方向 | NLP、神经网络

在这篇文章中，我们将探讨一个被称为“梯度流（Gradient Flow）”的概念。简单来说，梯度流是将我们在用梯度下降法中寻找最小值的过程中的各个点连接起来，形成一条随（虚拟的）时间变化的轨迹，这条轨迹便被称作“梯度流”。在文章的后半部分，我们将重点讨论如何将梯度流的概念扩展到概率空间，从而形成“Wasserstein 梯度流”，为我们理解连续性方程、Fokker-Planck 方程等内容提供一个新的视角。

梯度下降

假设我们想搜索光滑函数 的最小值，常见的方案是梯度下降（Gradient Descent），即按照如下格式进行迭代：

如果 关于 是凸的，那么梯度下降通常能够找到最小值点；相反，则通常只能收敛到一个“驻点”——即梯度为 0 的点，比较理想的情况下能收敛到一个极小值（局部最小值）点。这里没有对极小值和最小值做严格区分，因为在深度学习中，即便是收敛到一个极小值点也是很难得的了。

如果将 记为 ，将 记为，那么考虑 的极限，那么式（1）将变为一个 ODE：

求解这个 ODE 所得到的轨迹 ，我们就称为“梯度流（Gradient Flow）”，也就是说，梯度流是梯度下降在寻找最小值过程中的轨迹。在式（2）成立前提下，我们还有：

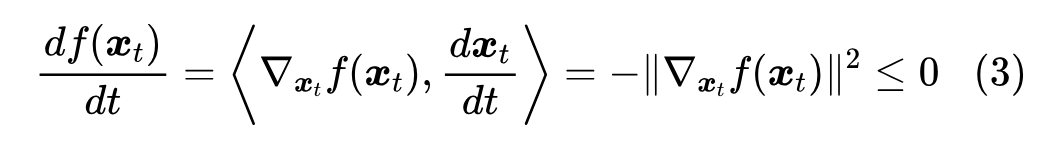
这就意味着，只要 ，那么当学习率足够小时，梯度下降总能往让 变小的方向前进。

更多相关讨论，可以参考之前的优化算法系列，如《从动力学角度看优化算法：从SGD到动量加速》、《从动力学角度看优化算法：一个更整体的视角》等。

最速方向

为什么要用梯度下降？一个主流的说法是“梯度的负方向是局部下降最快的方向”，直接搜这句话就可以搜到很多内容。这个说法不能说错，但有点不严谨，因为没说明前提条件——“最快”的“最”必然涉及到定量比较，只有先确定比较的指标，才能确定“最”的结果。

如果只关心下降最快的方向的话，梯度下降的目标应该是：