给定数据集:, 其中
,
样本均值和样本方差的矩阵表达
样本均值:
, 这里记
样本方差:
记,
称之为centering matrix, 则
讨论:centering matrix的性质:
由可知,
综上可知,
最大投影方差角度
PCA的核心思想:将一组可能线性相关的变量通过正交变换成一组线性无关的变量;
- 一个中心:原始特征空间的重构(相关到无关)
- 两个基本点:
- 最大投影方差
- 最小重构距离
首先,对所有数据样本进行去中心化,即, 同时令投影方向
, 则投影方差:
, 此处
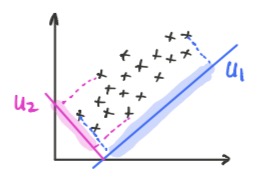
损失函数 , 同时
, 因为
,所以可写成这样
综上可知,
拉格朗日函数:
由,可得
,这里
为eign-vector,
为eign-value;
最小重构距离角度
首先,对所有样本进去中心化,即, 同时令投影方向
,
考虑二维的重构向量:, 其中
为投影标量,
为方向向量;如下图所示:
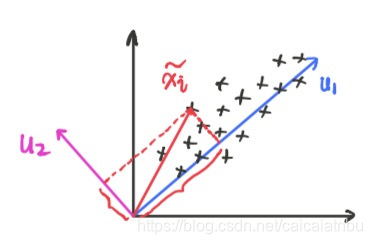
更一般的情况, , 则重构向量:
降维后,, 则重构向量:
, 降维是丢掉了一部分信息
重构距离为:
, 由上
可知,
综上可知,
由拉格朗日函数同理可得,
, 找出对重构距离影响最小的(p-q)个维度。
SVD 角度
,
,
, SVD分解,其中:
是对角矩阵;
综合与
, 可知,
和
有相同的特征值:(
,
为特征值构成的对角矩阵)。
特征分解
得到方向(主成分)
由
求做坐标【备注:
】
特征分解
直接求得坐标
由可知,
, 其中
,
为特征值
组成的对角矩阵。
为T的特征向量
组成的矩阵,
直接求
的特征向量,就可以直接得到坐标;
当 时,分解
, 当
时,分解
;
完,





 本文详细探讨了PCA(主成分分析)的核心概念,包括样本均值和方差的矩阵表达,最大投影方差角度,最小重构距离角度以及SVD的角度。PCA旨在通过正交变换将数据转换为线性无关的变量,最大化投影方差并最小化重构距离。通过对数据进行去中心化,利用拉格朗日乘子法寻找最优投影方向,以及SVD分解来确定主成分。
本文详细探讨了PCA(主成分分析)的核心概念,包括样本均值和方差的矩阵表达,最大投影方差角度,最小重构距离角度以及SVD的角度。PCA旨在通过正交变换将数据转换为线性无关的变量,最大化投影方差并最小化重构距离。通过对数据进行去中心化,利用拉格朗日乘子法寻找最优投影方向,以及SVD分解来确定主成分。
















 7532
7532

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








