纵波时差预测

爱找石油的小孩

已于 2024-10-28 17:55:47 修改

阅读量662

点赞数 27

文章标签：人工智能算法机器学习

于 2024-10-28 10:52:37 首次发布

本文链接：https://blog.csdn.net/caoqichang_sir/article/details/143284745

版权

（本报告为课程作业欢迎大家讨论）

摘要

本报告旨在展示通过对MULTI WELLS中的数据进行清洗和处理，利用随机森林法构建预测纵波时差（DT）模型的过程。首先，我们对原始数据进行了系统的数据清洗，以去除重复和异常值，确保数据的质量和准确性。接着，使用随机森林算法构建了DT的预测模型，利用已清洗的数据进行训练。

在模型构建完成后，我们对Prediction in blind well文件中的数据进行了相同的数据清洗流程，以准备进行预测。最后，通过比较预测值与原始值的差异，我们对模型的预测质量进行了评估。结果表明，随机森林法在DT值的预测上具有良好的性能。

一、数据预处理

数据清洗

对MULTI WELLS文件中WELL-01和WELL-07井中所测得的数据清洗，具体操作包括：去除重复值、去除异常值

数据去重

在文件中发现重复值较多，如果采用整体去重的操作得到的数据并不理想，这样去除的重复值只是“GR RHOB NPHI LLD DT DTS”这些数据完全重合时的数据，另一种清洗的方法是对每一种数据进行依次去重，如果一行中有一个数据重复就删除整个行，这样的操作导致文件清洗之后留下的可用数据点太少。

通过观察文件中数据我们可以发现在文件中大量存在的是部分数据重合。故采取以下去重操作：

以每五行为一个组来进行操作，而不是在所有行中进行全局查找，在这五行内检查重复值，如果有一个数据重复就删除整个行。这样的操作留下的可用数据较多，方便后续的模型训练。

去除异常值

去除异常值所用到的方法是删除异常值所用到的是z-score法：z-score（标准分数）是用于描述一个数据点相对于其均值的偏离程度的统计量。它表示该数据点在标准差单位下的偏差量，用于识别异常值。z-score 大于3或小于-3的数据点被视为异常值将被删除。

训练数据清洗前后形状对比：

需要预测数据清洗前后的形状对比：

数据清洗效果

对训练数据清洗前后的散点图对比

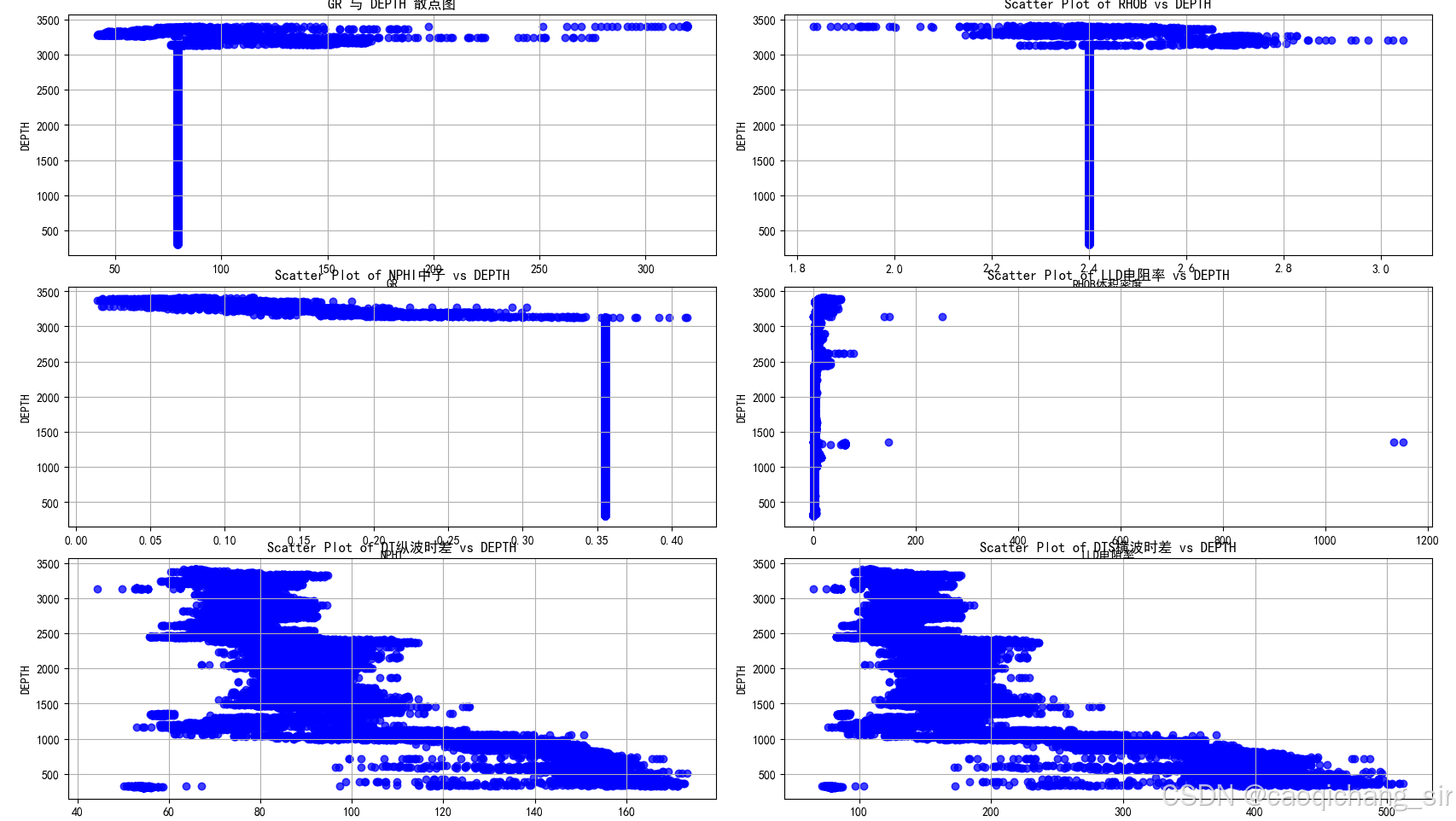
图1 未清洗数据

图2 清洗后数据

通过对比清洗前后的数据散点图分布发现经过数据清洗这一步骤去除了训练数据的中的重复值，数据的分布更直观。

预测模型建立

训练数据选取

考虑到横波DTS 和要预测的纵波DT的相关性过高特征占比过高故舍弃DTS，训练集和测试集所测得数据是同一地层所测得的数据，在相同的深度上对应着相同的地层特性因此将深度点DPTH作为一个训练元素考虑在内。综上选取的特征列是['GR', 'RHOB', 'NPHI', 'LLD','DEPTH'] 。

训练模型选取

考虑到此次要预测的横波DT与上述的特征列之间并不是线性关系，故选取随机森林回归的方法来进行模型的构建。

随机森林回归（Random Forest Regression）是一种集成学习方法，基于多棵决策树的组合来进行预测。它通过引入随机性来构建多棵独立的决策树，并将这些树的预测结果进行平均，从而提升模型的泛化能力并降低过拟合的风险。

随机森林回归的核心思想是通过引入两种随机性来创建一个强大的预测模型：

样本随机性：通过从原始数据集中有放回地随机抽取样本（即自助法或Bootstrap）来生成不同的训练数据集。
特征随机性：在构建每棵决策树时，随机选择部分特征来进行分裂。

随机森林回归的算法流程：

（1）样本抽取：从原始数据集中有放回地随机抽取多个样本，生成多个子数据集。

样本抽取公式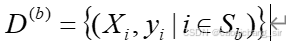：（不知道为什么在Word上做好的公式不能直接粘贴）

其中是第个子数据集的样本索引集合

（2）决策树构建：对于每个子数据集，使用决策树算法构建回归树。在每个节点分裂时，随机选择一部分特征，选择最佳特征进行分裂。

特征选择公式：

$eq?%5Ctext%7BSplit%20Feature%7D%20%3D%20%5Carg%5Cmin_%7Bj%20%5Cin%20%5Ctext%7BRandom%20Subset%7D%7D%20%5Csum_%7Bi%3D1%7D%5E%7Bm%7D%20%5Cleft%28%20y_i%20-%20%5Chat%7By%7D_i%20%5Cright%29%5E2$

3）集成预测：所有树训练完成后，对新输入的数据点，分别使用每棵决策树进行预测，然后对所有预测结果进行平均，得到最终的预测值。

最终预测公式：

$eq?%5Chat%7By%7D%5E%7B%28b%29%7D%28%5Cmathbf%7Bx%7D%29%20%3D%20%5Cfrac%7B1%7D%7B%7CL_b%28%5Cmathbf%7Bx%7D%29%7C%7D%20%5Csum_%7Bi%20%5Cin%20L_b%28%5Cmathbf%7Bx%7D%29%7D%20y_i$

其中， $eq?%5Chat%7By%7D%5E%7B%28b%29%7D%28%5Cmathbf%7Bx%7D%29$ 是第 $eq?b$ 棵决策树的预测结果。

随机森林回归的优缺点

优点：

高准确度：随机森林通过结合多棵决策树，显著提升了模型的预测准确度。

抗过拟合：由于引入了随机性，随机森林相比单棵决策树更加抗过拟合，能够更好地泛化到未见的数据。

能够处理高维数据：随机森林在特征维度较高的情况下仍然能够有效工作。

缺点：

计算复杂度高：由于随机森林需要训练多棵决策树，因此计算成本较高，尤其是在数据量大时。

模型解释性较差：随机森林的集成机制使得模型难以解释，不容易理解每个特征对预测结果的影响。

其特点符合本次预测横波DT值的要求。

预测结果

将预测的结果和真实值对比画图呈现如下

预测模型评估

1、模型评估参数

对于预测模型的评估主要从以下几个方面进行：

平均绝对误差 (MAE)：衡量预测值和真实值之间的平均绝对差距，反映了误差的平均水平。
均方误差 (MSE)：计算平方误差的平均值，MSE对较大误差更敏感，可以帮助识别较大误差的影响。
根均方误差 (RMSE)：是MSE的平方根，可以和MAE进行比较，以了解误差的分布
决定系数R²:用于判断模型解释数据方差的能力。决定系数R2越高，越接近于1，模型的拟合效果就越好

计算结果如下

Mean Absolute Error (MAE)	0.1396502082038519
Mean Squared Error (MSE)	0.06202726608065497
Root Mean Squared Error (RMSE)	0.24905273754900784
R-squared (R2)	0.99891370858001

2、评估结论

MAE 值较小，表明模型在平均上只存在约 0.14 的预测误差，说明模型的预测相对准确。
MSE 值也较低，说明预测值与真实值之间的平方差的平均值不大，表明模型对数据的拟合较好。
RMSE 是误差的标准差，约 0.25，意味着在所有预测值中，模型的预测误差在这个范围内。这个值相对较小，说明模型在预测方面表现良好。
R² 值接近 1，表明模型能够解释约 99.89% 的数据变异性。这个值非常高，表明模型拟合效果极佳。

综上所述，模型在预测 DT 值时表现出色，误差较小且拟合度高，适合用于实际应用和进一步的分析。这表明所构建的模型有效地捕捉了数据中的模式，能够可靠地进行预测。

附录：python代码

数据清洗

1.	import pandas as pd  
2.	import os  
3.	import numpy as np  
4.	from scipy import stats  
5.	  
6.	# 设置工作目录  
7.	os.chdir(r'C:\Users\Admin\Desktop\DEMO-03-第三次作业-预测纵波时差DT曲线\DEMO-03-第三次作业-预测DT和DTS曲线')  
8.	  
9.	file = 'MULTI WELLS.csv'  
10.	  
11.	# 数据读取  
12.	columns_to_read = ['DEPTH','GR', 'RHOB', 'NPHI', 'LLD', 'DT', 'DTS']  
13.	data = pd.read_csv(file, usecols=columns_to_read)  
14.	  
15.	# 打印原始数据的形状  
16.	print("原始数据形状：", data.shape)  
17.	  
18.	# 定义每批的大小（即每 5 行一组）  
19.	batch_size = 5  
20.	  
21.	# 定义一个空的 DataFrame，用于存储去重后的数据  
22.	cleaned_data = pd.DataFrame(columns=data.columns)  
23.	  
24.	# 逐批处理每 5 行  
25.	for i in range(0, len(data), batch_size):  
26.	    batch = data.iloc[i:i + batch_size]  # 提取每 5 行的数据  
27.	  
28.	    # 删除批次中任意列出现重复值的行  
29.	    # 删除任意一列中出现重复值的行  
30.	    batch_cleaned1 = batch.drop_duplicates(subset=['GR'], keep=False)  
31.	    batch_cleaned2 = batch_cleaned1.drop_duplicates(subset=['RHOB'], keep=False)  
32.	    batch_cleaned3 = batch_cleaned2.drop_duplicates(subset=['NPHI'], keep=False)  
33.	    batch_cleaned4 = batch_cleaned3.drop_duplicates(subset=['LLD'], keep=False)  
34.	    batch_cleaned5 = batch_cleaned4.drop_duplicates(subset=['DT'], keep=False)  
35.	    batch_cleaned = batch_cleaned5.drop_duplicates(subset=['DTS'], keep=False)  
36.	  
37.	    # 如果 batch_cleaned 为空则跳过该批次  
38.	    if batch_cleaned.empty:  
39.	        continue  
40.	  
41.	    # 将非空的 batch_cleaned 拼接到 cleaned_data  
42.	    cleaned_data = pd.concat([cleaned_data, batch_cleaned])  
43.	  
44.	# 打印清洗后的数据形状  
45.	print("清洗重复值后的数据形状：", cleaned_data.shape)  
46.	  
47.	  
48.	# 使用 Z-score 检测并删除异常值  
49.	# 计算每列的 Z-score  
50.	z_scores = np.abs(stats.zscore(cleaned_data.select_dtypes(include=[np.number])))  # 只计算数值列的 z-score  
51.	  
52.	# 设置 Z-score 阈值，通常 3 是一个常用的值  
53.	threshold = 3  
54.	  
55.	# 删除 z-score 超过阈值的行  
56.	cleaned_data = cleaned_data[(z_scores < threshold).all(axis=1)]  
57.	  
58.	# 打印清洗后（去除异常值）的数据形状  
59.	print("清洗异常值后的数据形状：", cleaned_data.shape)  
60.	  
61.	# 保存清洗后的数据（可选）  
62.	cleaned_data.to_csv('cleaned_well_data_with_zscore.csv', index=False)

2、散点图绘制

1.	import pandas as pd  
2.	import numpy as np  
3.	import os  
4.	import matplotlib.pyplot as plt  
5.	import matplotlib  
6.	  
7.	# 设置中文字体  
8.	matplotlib.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体  
9.	matplotlib.rcParams['axes.unicode_minus'] = False  # 使负号正常显示  
10.	  
11.	# 设置工作目录  
12.	os.chdir(r'C:\Users\Admin\Desktop\DEMO-03-第三次作业-预测纵波时差DT曲线\DEMO-03-第三次作业-预测DT和DTS曲线')  
13.	  
14.	file = 'cleaned_well_data_with_zscore.xlsx'  # 确认文件名没有多余空格或错别字  
15.	  
16.	# 数据读取  
17.	columns_to_read = ['GR', 'RHOB', 'NPHI', 'LLD', 'DT', 'DTS', 'DEPTH']  
18.	try:  
19.	    data = pd.read_excel(file, usecols=columns_to_read)  
20.	except FileNotFoundError:  
21.	    print(f"文件 {file} 未找到，请检查路径和文件名。")  
22.	    raise  
23.	  
24.	# 绘制散点图  
25.	plt.figure(figsize=(10,25))  # 设置图形大小  
26.	  
27.	# 第一个子图：GR vs DEPTH  
28.	plt.subplot(3, 2, 1)  # 3行2列的第1个图  
29.	plt.scatter(data['GR'], data['DEPTH'], color='blue', alpha=0.2)  
30.	plt.title('GR 与 DEPTH 散点图')  
31.	plt.xlabel('GR')  
32.	plt.ylabel('DEPTH')  
33.	  
34.	plt.grid(True)  
35.	  
36.	  
37.	  
38.	plt.subplot(3, 2, 2)  # 3行2列的第2个图  
39.	plt.scatter(data['RHOB'], data['DEPTH'], color='blue', alpha=0.2)  
40.	plt.title('Scatter Plot of RHOB vs DEPTH')  
41.	plt.xlabel('RHOB体积密度')  
42.	plt.ylabel('DEPTH')  
43.	plt.grid(True)  
44.	  
45.	plt.subplot(3, 2, 3)  # 3行2列的第3个图  
46.	plt.scatter(data['NPHI'], data['DEPTH'], color='blue', alpha=0.2)  
47.	plt.title('Scatter Plot of NPHI中子 vs DEPTH')  
48.	plt.xlabel('NPHI')  
49.	plt.ylabel('DEPTH')  
50.	plt.grid(True)  
51.	  
52.	plt.subplot(3, 2, 4)  # 3行2列的第4个图  
53.	plt.scatter(data['LLD'], data['DEPTH'], color='blue', alpha=0.2)  
54.	plt.title('Scatter Plot of LLD电阻率 vs DEPTH')  
55.	plt.xlabel('LLD电阻率')  
56.	plt.ylabel('DEPTH')  
57.	plt.grid(True)  
58.	  
59.	plt.subplot(3, 2, 5)  # 3行2列的第5个图  
60.	plt.scatter(data['DT'], data['DEPTH'], color='blue', alpha=0.2)  
61.	plt.title('Scatter Plot of DT纵波时差 vs DEPTH')  
62.	plt.xlabel('DT纵波时差')  
63.	plt.ylabel('DEPTH')  
64.	plt.grid(True)  
65.	  
66.	plt.subplot(3, 2, 6)  # 3行2列的第6个图  
67.	plt.scatter(data['DTS'], data['DEPTH'], color='blue', alpha=0.2)  
68.	plt.title('Scatter Plot of DTS横波时差 vs DEPTH')  
69.	plt.xlabel('DTS横波时差')  
70.	plt.ylabel('DEPTH')  
71.	plt.grid(True)  
72.	  
73.	# 调整布局以避免重叠  
74.	plt.tight_layout()  
75.	plt.show()  # 显示图形

3 随机森林预测模型

1.	from sklearn.datasets import fetch_california_housing  
2.	from sklearn.model_selection import train_test_split  
3.	from sklearn.ensemble import RandomForestRegressor  
4.	from sklearn.metrics import mean_squared_error, r2_score  
5.	import pandas as pd  
6.	import numpy as np  
7.	import os  
8.	  
9.	# 设置工作目录  
10.	os.chdir(r'C:\Users\Admin\Desktop\DEMO-03-第三次作业-预测纵波时差DT曲线\DEMO-03-第三次作业-预测DT和DTS曲线')  
11.	  
12.	# 读取训练数据  
13.	train_file = 'cleaned_well_data_with_zscore.xlsx'  
14.	train_columns = ['GR', 'RHOB', 'NPHI', 'LLD','DEPTH']  # 特征列  
15.	X_train = pd.read_excel(train_file, usecols=train_columns)  # 特征  
16.	y_train = pd.read_excel(train_file, usecols=['DT'])  # 目标列  
17.	  
18.	#定义随机森林回归模型  
19.	# 定义随机森林回归模型  
20.	rfr = RandomForestRegressor(n_estimators=100, random_state=42)  
21.	  
22.	# 训练模型  
23.	rfr.fit(X_train, y_train)  
24.	  
25.	  
26.	# 读取要预测的数据  
27.	predict_file = 'cleaned_well_prediction_data.csv'  
28.	X_predict = pd.read_csv(predict_file, usecols=train_columns)  # 选择与训练特征相同的列  
29.	y_first = pd.read_csv(predict_file,usecols=['DT'])  
30.	# 使用模型进行预测  
31.	y_pred = rfr.predict(X_predict)  
32.	  
33.	# 将预测结果保存到新的 Excel 文件中  
34.	predicted_data = pd.DataFrame(X_predict)  # 保留原始特征列  
35.	predicted_data['Predicted_DT'] = y_pred  # 增加一列保存预测的DT值  
36.	predicted_data['DT'] = y_first #增加一列保存训练值  
37.	  
38.	# 保存结果到 Excel 文件  
39.	predicted_data.to_csv('cleaned_well_prediction_data.csv', index=False)  
40.	print('预测完成并已保存到 cleaned_well_prediction_data.csv')

4 预测模型数据对比

1.	import pandas as pd  
2.	import numpy as np  
3.	import os  
4.	import matplotlib.pyplot as plt  
5.	import matplotlib  
6.	from sklearn.metrics import r2_score  
7.	from sklearn.metrics import mean_absolute_error  
8.	  
9.	  
10.	# 设置中文字体  
11.	matplotlib.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体  
12.	matplotlib.rcParams['axes.unicode_minus'] = False  # 使负号正常显示  
13.	  
14.	# 设置工作目录  
15.	os.chdir(r'C:\Users\Admin\Desktop\DEMO-03-第三次作业-预测纵波时差DT曲线\DEMO-03-第三次作业-预测DT和DTS曲线')  
16.	  
17.	file = 'cleaned_well_prediction_data.csv'  # 确认文件名没有多余空格或错别字  
18.	  
19.	# 数据读取  
20.	try:  
21.	    data = pd.read_csv(file, encoding='ISO-8859-1')  # 或者尝试 'GBK'  
22.	except Exception as e:  
23.	    print(f"读取文件时发生错误: {e}")  
24.	  
25.	  
26.	y1 = data['Predicted_DT']  # 预测的DT值  
27.	y2 = data['DT']  # 初始DT值  
28.	index_values = data['DEPTH']  # 深度  
29.	  
30.	#R2  
31.	r2_1= r2_score(y2, y1)  
32.	print(f"R² Score: {r2_1}")  
33.	  
34.	# 绘制散点图  
35.	plt.figure(figsize=(9,15))  # 调整图形大小  
36.	  
37.	  
38.	# 第一个子图：  
39.	plt.subplot(1,3, 1)  # 3行2列的第1个图# 绘制线条和数据点  
40.	plt.plot(y1, index_values, color='b', label='Predicted_DT', linestyle='-')  
41.	plt.plot(y2, index_values, color='r', label='原始DT值', linestyle='-')  
42.	# 反转纵轴  
43.	plt.gca().invert_yaxis()  
44.	# 添加标题和标签  
45.	plt.title('数据大小与深度关系图')  
46.	plt.xlabel('DT')  
47.	plt.ylabel('Depth')  
48.	plt.legend()  
49.	plt.grid()  
50.	  
51.	#第二个图  
52.	plt.subplot(1,3,2)  # 3行2列的第1个图# 绘制线条和数据点  
53.	plt.plot(y2, index_values, color='r', label='原始DT值', linestyle='-')  
54.	plt.gca().invert_yaxis()  
55.	plt.title('DT 与 DEPTH 散点图')  
56.	plt.xlabel('DT')  
57.	plt.ylabel('DEPTH')  
58.	plt.legend()  
59.	plt.grid()  
60.	#第三个图  
61.	plt.subplot(1,3,3)  # 3行2列的第1个图# 绘制线条和数据点  
62.	plt.plot(y1, index_values, color='b', label='Predicted_DT', linestyle='-')  
63.	plt.gca().invert_yaxis()  
64.	plt.title('Predicted_DT 与 DEPTH 散点图')  
65.	plt.xlabel('Predicted_DT')  
66.	plt.ylabel('DEPTH')  
67.	plt.legend()  
68.	plt.grid()  
69.	  
70.	plt.show()

5 模型评估

1.	from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score  
2.	import numpy as np  
3.	import pandas as pd  
4.	import matplotlib  
5.	import os  
6.	  
7.	# 设置中文字体  
8.	matplotlib.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体  
9.	matplotlib.rcParams['axes.unicode_minus'] = False  # 使负号正常显示  
10.	  
11.	# 设置工作目录  
12.	os.chdir(r'C:\Users\Admin\Desktop\DEMO-03-第三次作业-预测纵波时差DT曲线\DEMO-03-第三次作业-预测DT和DTS曲线')  
13.	  
14.	file = 'cleaned_well_prediction_data.csv'  # 确认文件名没有多余空格或错别字  
15.	data = pd.read_csv(file, encoding='ISO-8859-1')  # 或者尝试 'GBK'  
16.	  
17.	# 假设 y_true 和 y_pred 是真实值和预测值的数组或序列  
18.	y_true = data['DT']# 真实数据  
19.	y_pred =data['Predicted_DT'] # 预测数据  
20.	  
21.	# 计算各个指标  
22.	mae = mean_absolute_error(y_true, y_pred)  
23.	mse = mean_squared_error(y_true, y_pred)  
24.	rmse = np.sqrt(mse)  
25.	r2 = r2_score(y_true, y_pred)  
26.	  
27.	print(f"Mean Absolute Error (MAE): {mae}")  
28.	print(f"Mean Squared Error (MSE): {mse}")  
29.	print(f"Root Mean Squared Error (RMSE): {rmse}")  
30.	print(f"R-squared (R2): {r2}")

随机森林回归的算法流程部分引用自用Python实现9大回归算法详解——08. 随机森林回归算法_随机森林回归模型-CSDN博客