82岁的北大教授证明了黎曼猜想？

来源：AI科技大本营

最近，黎曼猜想有点热。

上个月，89 岁的菲尔兹奖与阿贝尔奖双料得主、英国皇家学会院士迈克尔·阿蒂亚爵士（Michael Atiyah）刚刚宣布自己证明了黎曼猜想。

近日，82 岁的北大教授（已退休）李忠也要挑战黎曼猜想。

真真是老当益壮。

10 月 9 日，南方科技大学副校长汤涛教授在微博上转发一则公告，称北京大学的李忠教授将在 10 月 11 日挑战“黎曼猜想”。

      

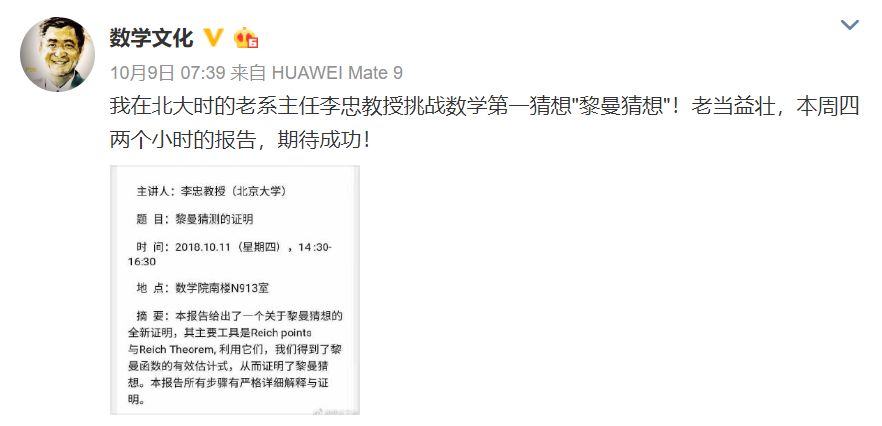
公告摘要显示，李忠教授将在报告中给出一个关于黎曼的全新证明，其主要工具是 Reich points 与 Reich Theorem，利用它们得到了黎曼函数的有效估计式，从而证明了黎曼猜想。重点是，本报告所有步骤有严格详细解释与证明。

              

随后，有人质疑称这个消息是假的，因为北大数院的楼只有 8 层没有 9 层。不过知乎用户、某高校老师 @gujurat 称，这个报告预告是真实的，并不是从李忠老师以前的报告预告 p 的。报告原定是中科院数学所南楼，不是北大数学院，所以 9 楼并不是什么问题，而预告里的地点是动力系统讨论班的一个固定场所。

不过，根据最新得到的消息，这次报告已经取消，因为李老师的学生里有人发现了证明中的错误。当然，李老师还是比较坚持认为自己是对的，不过在解决疑问之前先把报告取消。

▌关于李忠教授

公开资料显示，李忠 1960 年毕业于北京大学数学力学系，随即留校任教。1979 年至 1981 年 间，他在瑞士苏黎世大学数学研究所访学。李忠 1980 年升为副教授，1985 年评为教授、博士生导师，1987 年至 1991 年担任北京大学数学系主任。其研究领域为基础数学复分析，对拟共形映射与黎曼曲面的模空间理论有系统的研究。

其研究成果曾获得国家教委科技进步奖（一等奖），并两次获得国家自然科学奖（三等奖）。1991 年被国家人事部与国家教委评为“有突出贡献的中青年专家”。1993 年被国家教委评为“国家优秀教师”。

此外，李忠教授还编写过复分析导引和高等数学教程。据说，李忠老师编写的高等数学教程比流行的同济版高数教程更难。

              

在去年 9 月的一次学术讲座上，李忠教授曾以《数学的新黄金时代》为题，论述了计算机在数学领域的利用以及数学与计算机的相关联性，并就四色问题、NP 问题、黎曼猜想等用计算机解决的问题或与计算机有关的数学问题进行论证。

不过就连阿蒂亚爵士在海德堡获奖者论坛上的报告也饱受质疑，李忠教授对黎曼猜想的证明真的靠谱吗？

由于这次报告已经取消，所以我们也无从得知李忠教授的论证细节。不过 @gujurat 表示，用厄米特矩阵特征值来表征黎曼函数的想法早已有之，也是现在被尝试很多的一个方法。从这个观点来看，Reich 定理可能确实与之有关。而李忠老师作为知名复分析专家，对此理论熟悉也不奇怪。暂时来看细节上可能有问题，但至少能提供一个可能的研究方向。

▌关于黎曼猜想

黎曼猜想（或称黎曼假设）是关于黎曼ζ函数ζ(s)的零点分布的猜想，由数学家波恩哈德·黎曼于1859 年提出。德国数学家戴维·希尔伯特在第二届国际数学家大会上提出了20世纪数学家应当努力解决的 23 个数学问题，其中便包括黎曼假设。现今克雷数学研究所悬赏的世界七大数学难题中也包括黎曼假设。 

黎曼猜想是当今数学界最重要的数学难题，当今数学文献中已有超过一千条数学命题以黎曼猜想（或其推广形式）的成立为前提。2000 年，美国克莱数学研究所将黎曼猜想列为千禧年七大数学难题之一，成功解决其中任何一个难题都将获得 100 万美元奖金。

据报道，曾有人统计，在当今数学文献中已有超过一千条数学命题以黎曼猜想（或其推广形式）的成立为前提。如果黎曼猜想被证明，所有那些数学命题就全都可以荣升为定理；反之，如果黎曼猜想被否证，则那些数学命题中起码有一部分将成为陪葬。

黎曼猜想自 1859 年“诞生”至今，无数数学家都希望能攻克这一难题。然而，至今没有人给出解答，反倒是出了不少闹剧。

比如，英国在 2015 年曾报道，尼日利亚教授奥派耶米 伊诺克(Opeyemi Enoch)成功解决已存在156年的数学难题——黎曼猜想。然而随后便有人指出，这很可能是一场自导自演的闹剧，最终不了了之。

今年 9 月，阿蒂亚爵士声明证明黎曼猜想，并在海德堡获奖者论坛上进行了宣讲。然而 ，在为时 45 分钟的演讲过程中，25 分钟都是在回顾历史，只有一页 PPT 是证明相关。

虽然阿蒂亚爵士有很高的威望，但是学术界对此次演讲质疑声普遍较高。至于网上泄露出来的疑似论文也没能让人信服。

著名科普作者卢昌海评论称，

（阿蒂亚爵士的）报告录像给我一种交杂的感觉， 一开始讲述历史的部分是有一定条理， 甚至有一定幽默的——那句 “Solve the Riemann hypothesis and you become famous. If you are famous already, you become infamous” （解决黎曼猜想，你会变得声名显赫，如果你已经声名显赫，你会变得声名狼藉） 更是堪称整个报告的唯一亮点。 然而到了证明黎曼猜想的部分， 从试图用数学解释 “精细结构常数” （这个物理常数的数值其实跟能标有关， 并非数学意义上的常数） 这个本身就很突兀的努力， 突兀地转到以一张透明片的篇幅宣称证明黎曼猜想，这一刻，我相信满座听众绝无一人明白他的意思。

     

      阿蒂亚爵士 “疑似” 论文的核心部分

至于那篇题为 “黎曼猜想” (The Riemann Hypothesis) 的总计 5 页的 “疑似” 论文， 它是否是阿蒂亚爵士的正式论文，目前尚无定论，不过可能性不小，一是风格跟阿蒂亚爵士的近期论文比较相似，二是阿蒂亚爵士在报告末尾答听众问题时提到论文恰是 5 页。跟报告中的那一张透明片相比，论文稍体面些，但依然存在明显问题。拣小的说，几天前的通告中提到的狄拉克在论文中未曾出现，呈前言不搭后语之感；2.6 这个标号则出现了两次， 显得粗疏和草率。拣大的说， 从 2.6 到 3.3 这大半页的核心推理——也就是对黎曼猜想的 “证明”——完全推不动。而且哪怕姑妄读之，推特上也已有读者注意到，整个过程没有用到黎曼 ζ 函数的任何特殊性质，从而要么是错误的， 要么适用于在所讨论区域内解析性质相同的任何函数， 难不成所有那些函数的零点全归黎曼猜想管？

卢昌海猜测，如果哪天真有哪位数学家证明了黎曼猜想，在他自拟的标题里，你也许根本不会看到最耸人听闻的 “黎曼猜想” 的字眼，而是会像怀尔斯证明费马猜想的首个报告取名为 “模形式、椭圆曲线及伽罗瓦表示”，或佩雷尔曼证明庞加莱猜想的首篇论文取名为 “里奇流的熵公式及其几何应用” 那样的低调。 

             

参考来源：

https://weibo.com/p/1005051892680923/home?profile_ftype=1&is_all=1#_0

https://www.zhihu.com/question/297707301/answer/507756643（已获知乎作者授权）

https://www.changhai.org/articles/miscellaneous/comments/riemann3.php（按照卢昌海老师版权声明格式转载）

https://weibo.com/ChanghaiBlog?profile_ftype=1&is_all=1#_0

未来智能实验室是人工智能学家与科学院相关机构联合成立的人工智能，互联网和脑科学交叉研究机构。

未来智能实验室的主要工作包括：建立AI智能系统智商评测体系，开展世界人工智能智商评测；开展互联网（城市）云脑研究计划，构建互联网（城市）云脑技术和企业图谱，为提升企业，行业与城市的智能水平服务。

  如果您对实验室的研究感兴趣，欢迎加入未来智能实验室线上平台。扫描以下二维码或点击本文左下角“阅读原文”