黎曼猜想？

的所有非平凡零点都在Re=1/2的这条线上。

这就是黎曼的猜想。

介绍黎曼猜想之前先看看数学界关于素数（质数）的研究：素数就是只有1和本身的约数就是素数。

1、素数的研究

欧几里得定理，证明了素数是无穷多了：（反证法）

人们如何获取质数，（埃及）埃拉拖色尼筛选法：

 

 继续发展，既然素数有无限多个，有没有公式知道素数在一定范围的公式：

2、素数计数函数（Prime-counting function）（高斯勒让德公式）

 

 3、德国数学家（黎曼出现）

格奥尔格·弗雷德里希·波恩哈德·黎曼（1826－1866）德国数学家，黎曼几何学创始人，复变函数论创始人之一。1859年被任命为柏林科学院通讯院士，提交了一篇关于数论的论文，《论小于一个给定值的素数个数》。

 黎曼居然给出了素数计数函数的准确表达式：

 这个函数分为两部分：

说一下黎曼函数 ：

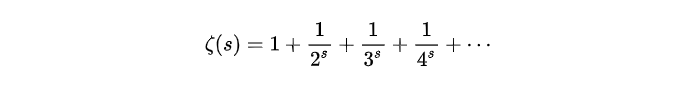
 函数领域使用x，复数领域使用s。

 =0；

有无数个根，总体可以分为俩类。

（1）平凡解，s=-2n,也就是所有负偶数。这个解看上去就比较简单，也很容易求，所以叫做平凡解，也叫做 函数的平凡零点。

（2）非平凡解：s=a+bi，也就是复数解，也就是非平凡零点的解。

黎曼的猜想就是非平凡零点的实部re=1/2。

4、黎曼素数计数函数

 

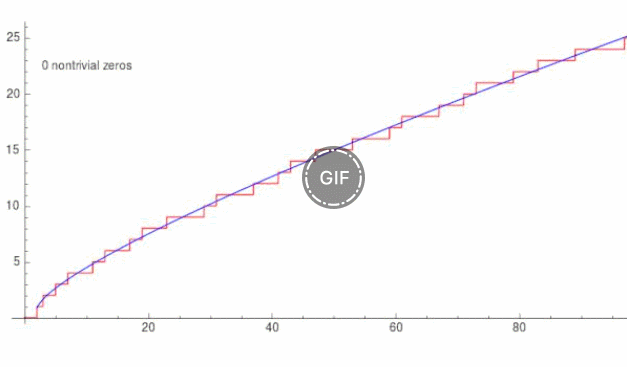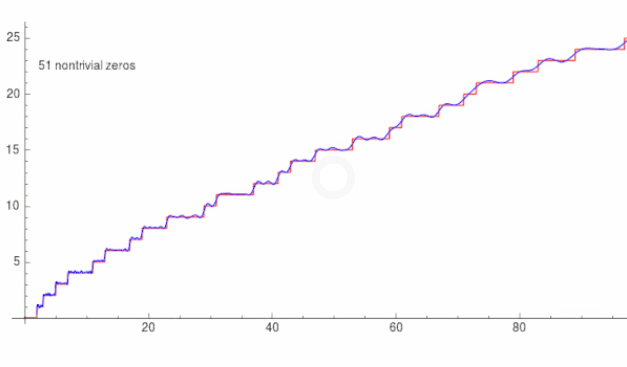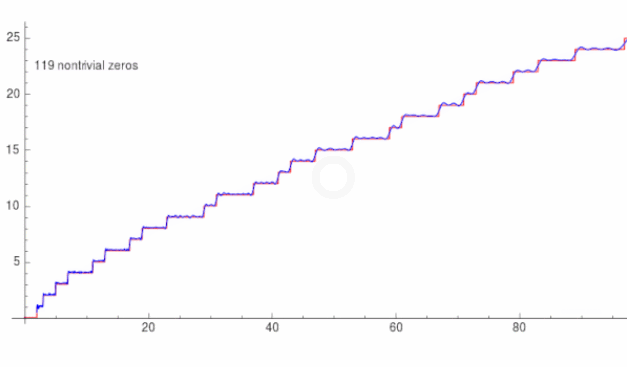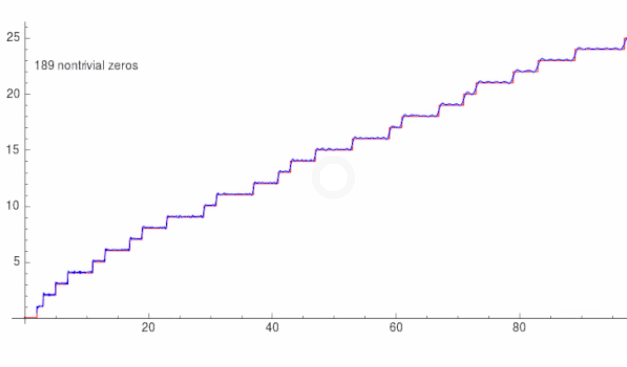
5、 是如何扩展到复数域的？

大家也都知道欧拉推出一个等式，所有自然数的和最后计算到-1/12?

 

 

黎曼函数 的定义域是s>1,sR    Re(s)>1,sC,实数大于1，后来解析为复数，只要复数的实部大于1都可以。

注意：要证明黎曼猜想的注意定义域。后来黎曼通过解析延拖，也就是函数处处可导，延拖之s<1。通过解析延拖：

=-1/12

=0

=1/120

 6、黎曼猜想的发展

1、1896年法国学者阿达玛.普森，证明了Re（s）（0,1），黎曼猜想的实部都在0~1之间。

2、1903年，格拉姆计算出15个非平凡零点都在1/2上，后来计算了138个全部满足黎曼猜想。

3、1932年，西格尔研究黎曼手稿，黎曼以前遗留下来的，研究出来西格尔黎曼公式

4、1936年计算机计算出来1041个非平凡零点；1953年计算出来1104个 ；1982年计算出来3亿个非平凡零点；IMB的公益活动计算零点（zetaGird）共计算出来1万亿个零点。

到目前为止黎曼猜想都还是正确的。

。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。

复分析数学还是比较值得关注，复数更加贴近自然，更加贴近宇宙的规律。

曾经在想，为什么需要研究质数，从宇宙的角度来看，质数相当于一个独立的星系或者组织，没有子系统；合数相当于有很多个子系统，比如太阳系（好多行星），行星下又有卫星，是不是特别的形象。加油oligei！！！！！！！！！！！！！！！

期待有人可以证明黎曼猜想。有部分图片来自网上，希望留言讨论撒！！！！！！！！