黎曼猜想简介

世界七大数学难题， 是七个由美国克雷数学研究所(Clay Mathematics Institute,CMI) 于2000年5月24日公布的数学猜想。包括NP完全问题、霍奇猜想、庞加莱猜想、黎曼猜想、杨-米尔斯存在性和质量缺口、纳维-斯托克斯方程、BSD猜想。其中庞加莱猜想已被解决。这些难题是呼应1900年德国数学家大卫·希尔伯特在巴黎提出的23个数学问题，黎曼猜想是23个中唯一一个没被解决的。

1.在实数范围内：

黎曼函数如下表示，在实部大于1下，黎曼函数才收敛。

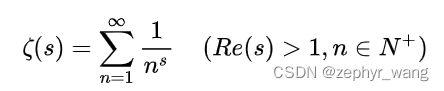
2.解析延拓至复数范围

黎曼函数如下表示（在s的实部不是大于1的时候）

3.黎曼函数等于0的情况

我们考虑黎曼函数等于0的情况，即

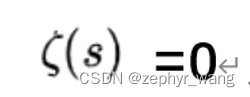
此外，

从这个关系式中不难发现，黎曼ζ 函数在 s=-2n (n 为正整数） 取值为零 - 因为 sin(πs/2) 为零 。这些零点分布有序、 性质简单， 被称为黎曼ζ 函数的平凡零点 (trivial zero)。除了这些平凡零点外，黎曼ζ 函数还有许多其它零点， 它们的性质远比那些平凡零点来得复杂， 被称为非平凡零点 (non-trivial zeros)。

4.黎曼猜想

黎曼猜想：黎曼ζ 函数的所有非平凡零点都位于复平面上 Re(s)=1/2 的直线上，也即方程ζ(s)=0的解的实部都是1/2。

数学家们把复平面上 Re(s)=1/2 的直线称为 critical line（临界线）。运用这一术语，黎曼猜想也可以表述为：黎曼ζ 函数的所有非平凡零点都位于 critical line 上。

5.黎曼猜想与素数定理

素数定理（prime number theorem）是素数分布理论的中心定理，是关于素数个数问题的一个命题： 设x≥1，以π(x)表示不超过x的素数的个数，当x→∞时，π(x)～x/ln(x)。

通过黎曼猜想可以证明素数定理。

1949年，塞尔伯格（即阿特勒·塞尔伯格，Atle Selberg）和埃尔德什（即保罗·埃尔德什，Paul Erdős）分别独立地证明了素数定理。与以往证明不同的是，他们没有用到ζ函数，而且除了极限、指数函数、对数函数的简单性质外，没有用到任何高等数学知识，甚至连微积分都没用到。