文章发表于:AAAI24
推荐指数: #paper/⭐⭐⭐
先验知识以及总结:
(参考毛海涛去年NeurIPS的文章文章链接)
以高的结构信息(英文high global structure proximity)(全局信息?不知道中文叫啥名字)为依据,取给异配图加边,会让图变得更加同配.
我自己的假设(不一定对),既然这样,我们按照局部信息(在某种意义上可以理解为特征相似性)(与高的结构信息相反)去删边,那么也会使图变得更加同配.本文就基于如上的推测
问题背景
问题:
以往的GNN都是基于同配图设计的
解决方法:
1.提出了软连接
2.图修剪模块和图增强模块被提出(目的:动态的删减/增加图的边让图适合同配性/异配性)
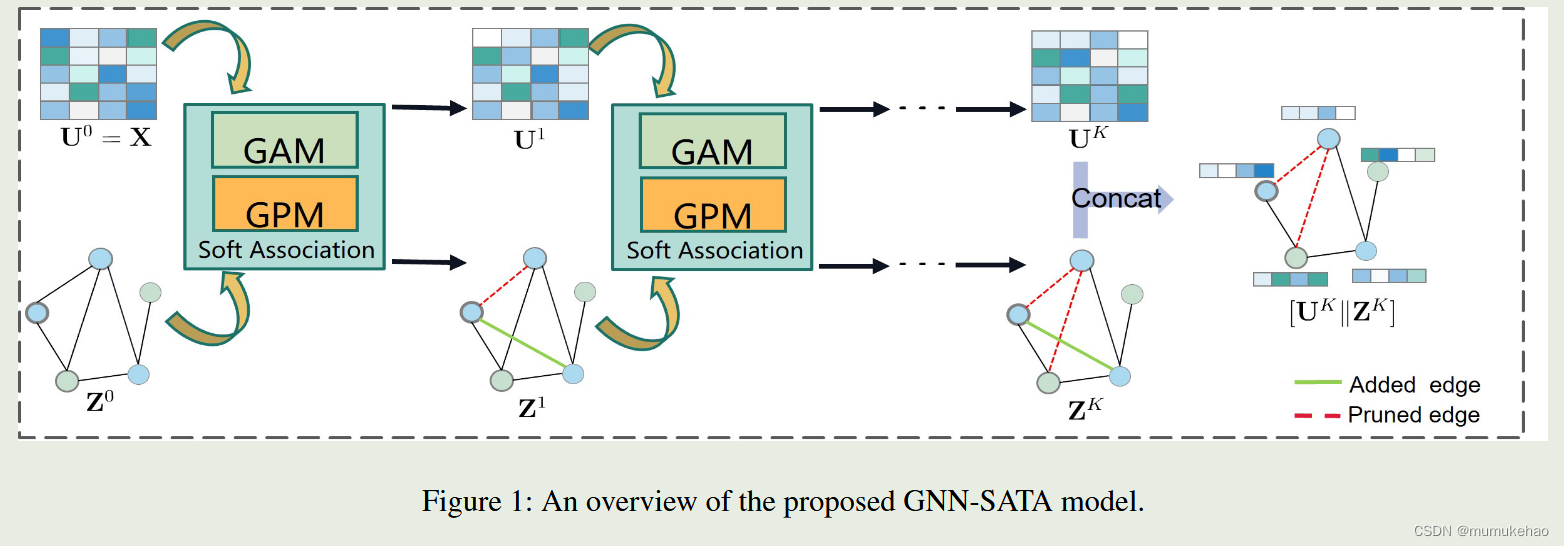
实验详情:
min
Z
,
U
∥
U
−
X
∥
F
2
+
α
1
tr
(
Z
⊤
L
~
Z
)
+
α
2
∥
U
U
⊤
−
A
∥
F
2
\min_{\mathbf{Z},\mathbf{U}}\left\|\mathbf{U}-\mathbf{X}\right\|_F^2+\alpha_1\operatorname{tr}\left(\mathbf{Z}^\top\tilde{\mathbf{L}}\mathbf{Z}\right)+\alpha_2\left\|\mathbf{U}\mathbf{U}^\top-\mathbf{A}\right\|_F^2
Z,Umin∥U−X∥F2+α1tr(Z⊤L~Z)+α2
UU⊤−A
F2
在这里,U和Z代表图数据的属性和拓扑表征,两者通过第三项连接.具体是,我们利用表征矩阵U去从特征提取相似性矩阵,让这个矩阵去接近原始的邻接矩阵A.
我们用
E
p
E_{p}
Ep取表示节点删除矩阵,
E
A
E_{A}
EA表示节点增加矩阵.这样,目标函数可以定义为:(1-A表示增加的其他边)
min
Z
,
U
,
E
P
,
E
A
∥
U
−
X
∥
F
2
+
α
1
tr
(
Z
⊤
L
~
A
Z
)
+
α
2
∥
U
U
⊤
−
(
A
⊙
E
P
+
(
1
−
A
)
⊙
E
A
)
∥
F
2
\begin{aligned}&\min_{\mathbf{Z},\mathbf{U},\mathbf{E}_P,\mathbf{E}_A}\left\|\mathbf{U}-\mathbf{X}\right\|_F^2+\alpha_1\operatorname{tr}\left(\mathbf{Z}^\top\tilde{\mathbf{L}}_\mathcal{A}\mathbf{Z}\right)\\&+\alpha_2\left\|\mathbf{U}\mathbf{U}^\top-(\mathbf{A}\odot\mathbf{E}_P+(\mathbf{1}-\mathbf{A})\odot\mathbf{E}_A)\right\|_F^2\end{aligned}
Z,U,EP,EAmin∥U−X∥F2+α1tr(Z⊤L~AZ)+α2
UU⊤−(A⊙EP+(1−A)⊙EA)
F2

M
=
[
U
K
∥
Z
K
]
\mathbf{M}=[\mathbf{U}^K\|\mathbf{Z}^K]
M=[UK∥ZK]
然后M可以用作半监督分类在线性变换和半监督分类任务后
L
=
∑
v
i
∈
V
L
ℓ
(
m
i
′
,
y
i
)
\mathcal{L}=\sum_{v_i\in\mathcal{V}_L}\ell\left(\mathbf{m}_i^{\prime},\mathbf{y}_i\right)
L=vi∈VL∑ℓ(mi′,yi)
(y,和m都是标签)
模型优化部分
min
Z
,
U
,
E
P
,
E
A
∥
U
−
X
∥
F
2
+
α
1
tr
(
Z
⊤
L
~
A
Z
)
+
α
2
∥
U
U
⊤
−
(
A
⊙
E
P
+
(
1
−
A
)
⊙
E
A
)
∥
F
2
\begin{aligned}&\min_{\mathbf{Z},\mathbf{U},\mathbf{E}_P,\mathbf{E}_A}\left\|\mathbf{U}-\mathbf{X}\right\|_F^2+\alpha_1\operatorname{tr}\left(\mathbf{Z}^\top\tilde{\mathbf{L}}_\mathcal{A}\mathbf{Z}\right)\\&+\alpha_2\left\|\mathbf{U}\mathbf{U}^\top-(\mathbf{A}\odot\mathbf{E}_P+(\mathbf{1}-\mathbf{A})\odot\mathbf{E}_A)\right\|_F^2\end{aligned}
Z,U,EP,EAmin∥U−X∥F2+α1tr(Z⊤L~AZ)+α2
UU⊤−(A⊙EP+(1−A)⊙EA)
F2
我们对上述公式求偏导,为了简化,我们让:
A
′
=
(
1
−
A
)
\mathbf{A^{\prime}}=(\mathbf{1-A})
A′=(1−A)以及:
A
=
A
⊙
E
P
+
A
′
⊙
E
A
)
\mathcal{A}=\mathbf{A}\odot\mathbf{E}_P+\mathbf{A}'\odot\mathbf{E}_A)
A=A⊙EP+A′⊙EA)
偏导结果如下:
2
(
U
−
X
)
+
2
α
2
(
2
U
U
⊤
−
A
ˉ
)
U
=
0
2
α
1
L
~
A
Z
=
0
V
P
+
2
α
2
(
−
A
⊙
U
^
P
+
A
⊙
A
⊙
E
P
)
=
0
V
A
+
2
α
2
(
−
A
′
⊙
U
^
A
+
A
′
⊙
A
′
⊙
E
A
)
=
0
\begin{aligned} &\begin{aligned}2(\mathbf{U}-\mathbf{X})+2\alpha_2(2\mathbf{U}\mathbf{U}^\top-\bar{\mathcal{A}})\mathbf{U}=0\end{aligned} \\ &2\alpha_1\mathbf{\tilde{L}}_A\mathbf{Z}=0 \\ &\begin{aligned}\mathbf{V}_P+2\alpha_2(-\mathbf{A}\odot\hat{\mathbf{U}}_P+\mathbf{A}\odot\mathbf{A}\odot\mathbf{E}_P)=0\end{aligned} \\ &\begin{aligned}\mathbf{V}_A+2\alpha_2(-\mathbf{A}'\odot\hat{\mathbf{U}}_A+\mathbf{A}'\odot\mathbf{A}'\odot\mathbf{E}_A)=0\end{aligned} \end{aligned}
2(U−X)+2α2(2UU⊤−Aˉ)U=02α1L~AZ=0VP+2α2(−A⊙U^P+A⊙A⊙EP)=0VA+2α2(−A′⊙U^A+A′⊙A′⊙EA)=0
在这里,
A
ˉ
\bar{\mathcal{A}}
Aˉ是规范化邻接矩阵
V
P
i
j
=
1
2
α
1
A
i
j
∥
Z
i
−
Z
j
∥
2
2
,
A
ˉ
,
V
A
i
j
=
1
2
α
1
A
i
j
′
∥
Z
i
−
Z
j
∥
2
2
,
U
^
P
=
U
U
⊤
−
A
′
⊙
E
A
,
U
^
A
=
U
U
⊤
−
A
⊙
E
P
\begin{align} \mathbf{V}_{Pij}=\frac12\alpha_1\mathbf{A}_{ij}\|\mathbf{Z}_{i}-\mathbf{Z}_{j}\|_2^2,\bar{\mathbf{A}},\mathbf{V}_{Aij}=\frac12\alpha_1\mathbf{A}_{ij}^{\prime}\|\mathbf{Z}_{i}-\mathbf{Z}_{j}\|_2^2, \\ \hat{\mathbf{U}}_{P}=\mathbf{UU}^{\top}-\mathbf{A}^{\prime}\odot\mathbf{E}_{A},\hat{\mathbf{U}}_{A}=\mathbf{UU}^{\top}-\mathbf{A}\odot\mathbf{E}_{P} \end{align}
VPij=21α1Aij∥Zi−Zj∥22,Aˉ,VAij=21α1Aij′∥Zi−Zj∥22,U^P=UU⊤−A′⊙EA,U^A=UU⊤−A⊙EP
这个迭代关系关于第k层和第k+1层模型可以表示为:
U
k
+
1
=
X
−
α
2
(
2
U
k
U
k
∣
−
A
ˉ
)
U
k
Z
k
+
1
=
A
ˉ
Z
k
E
P
k
+
1
=
(
2
α
2
A
⊙
U
^
P
k
−
V
P
k
)
/
(
2
α
2
A
⊙
A
)
E
A
k
+
1
1
=
(
2
α
2
A
′
⊙
U
^
A
k
−
V
A
k
)
/
(
2
α
2
A
′
⊙
A
′
)
\begin{aligned} &\mathbf{U}^{k+1}=\mathbf{X}-\alpha_2(2\mathbf{U}^\mathbf{k}\mathbf{U}^\mathbf{k}|-\bar{\mathcal{A}})\mathbf{U}^k \\ &\mathbf{Z}^{k+1}=\bar{\mathcal{A}}\mathbf{Z}^k \\ &\mathbf{E}_{P}^{k+1}=(2\alpha_{2}\mathbf{A}\odot\hat{\mathbf{U}}_{P}^{k}-\mathbf{V}_{P}^{k})/(2\alpha_{2}\mathbf{A}\odot\mathbf{A}) \\ &\mathbf{E}_A^{k+1}\begin{aligned}^1=(2\alpha_2\mathbf{A}^{\prime}\odot\hat{\mathbf{U}}_A^k-\mathbf{V}_A^k)/(2\alpha_2\mathbf{A'}\odot\mathbf{A'})\end{aligned} \end{aligned}
Uk+1=X−α2(2UkUk∣−Aˉ)UkZk+1=AˉZkEPk+1=(2α2A⊙U^Pk−VPk)/(2α2A⊙A)EAk+11=(2α2A′⊙U^Ak−VAk)/(2α2A′⊙A′)
V
i
j
k
=
1
2
α
1
A
i
j
∥
Z
i
k
+
1
−
Z
j
k
+
1
∥
2
2
,
U
^
k
=
U
k
+
1
U
k
+
1
−
A
′
⊙
E
A
\mathbf{V}_{ij}^k\quad=\quad\frac12\alpha_1\mathbf{A}_{ij}\|\mathbf{Z}_i^{k+1}-\mathbf{Z}_j^{k+1}\|_2^2,\quad\hat{\mathbf{U}}^k\quad=\mathbf{U}^{k+1}\mathbf{U}^{k+1} -\mathbf{A}^{\prime}\odot\mathbf{E}_A
Vijk=21α1Aij∥Zik+1−Zjk+1∥22,U^k=Uk+1Uk+1−A′⊙EA
为了增加模型的表达能力,我们将U的公式更正:
U
k
+
1
=
X
−
α
2
σ
[
(
2
U
k
U
k
⊤
−
A
ˉ
)
U
k
W
U
]
\mathbf{U}^{k+1}=\mathbf{X}-\alpha_2\sigma[(2\mathbf{U}^\mathbf{k}\mathbf{U}^\mathbf{k}\top-\bar{\mathcal{A}})\mathbf{U}^k\mathbf{W}_\mathbf{U}]
Uk+1=X−α2σ[(2UkUk⊤−Aˉ)UkWU]
U
k
U
k
⊤
−
A
ˉ
\mathbf{U^{k}U^k}^\top-\bar{\mathcal{A}}
UkUk⊤−Aˉ表示重构的邻接矩阵和邻接矩阵之间的差异,整个公式表示特征在消除差异同时保留共性的能力
实验结果
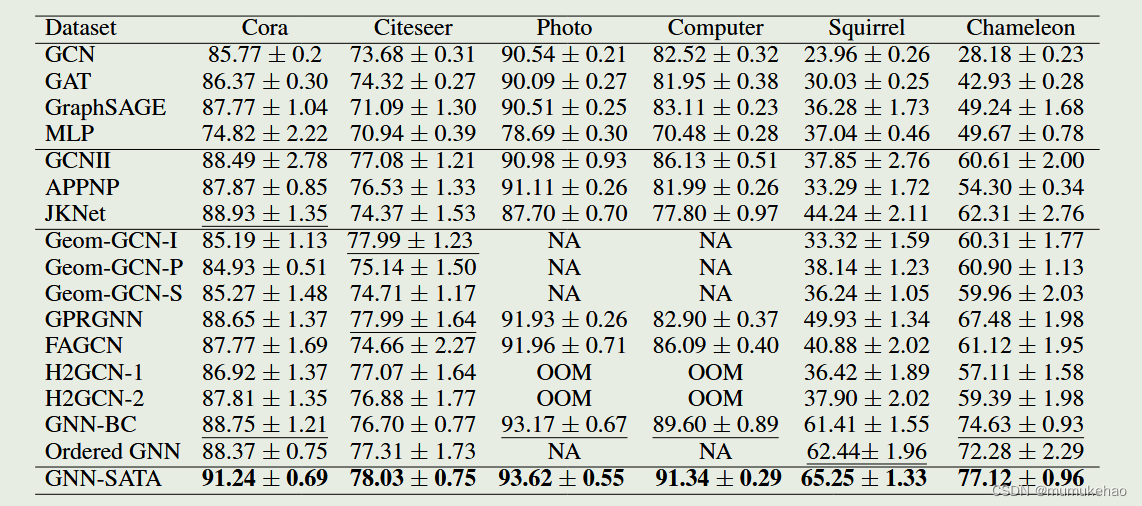
总结:
将Feature proximity 和Structure proximity结合,并利用自适应删边/加边,让两者逐渐趋同又存异,一个挺有意思的idea,理论上可以捕获更多的异配信息.
但是,实验只在两个异配图上做(Squirrel,Chameleon),仍需要部分实验证明其于其他数据集上也充分有效






















 7305
7305











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








