[论文学习笔记]01一种轮廓平行扫描算法【3D打印路径规划】

零.论文来源

Y. Yang,et al.Equidistant path generation for improving scanning efficiency in layered manufacturing[J].Rapid Prototyping Journa,2002,Volume 8 · Number 1:30-37.

0.1 概述

轮廓平行扫描是尺寸精度最佳的3D打印路径规划算法之一，这种算法沿着切片轮廓平行的方向逐层向内扫描，最大程度上保证了轮廓的精度，避免了台阶效应产生的失真等问题。这篇论文的作者把自己的方法称为“Equidistant path generation method”。

一.算法描述

1.1 定义一些概念

1.简单多边形：非相邻边彼此不相交的多边形。
图1

图1引用自 Y. Yang,et al.Equidistant path generation for improving scanning efficiency in layered manufacturing[J].Rapid Prototyping Journa,2002,Volume 8 · Number 1:30-37.

   数学表示：$e_i\cap e_j=\varnothing ,\forall j\ne i+1$
          其中$e_i、e_j$是多边形的边。

2.循环（cycle）和链（chain）：
1）循环是闭合的边界曲线，由有序的、首尾相连的线段组成。
2）链是多边形边界曲线上的线段。

3.循环深度：循环深度指的是轮廓包围的循环层数，可以用来刻画轮廓的复杂程度，可以画出深度树（图2）来形象的表示。如图2、3所示。
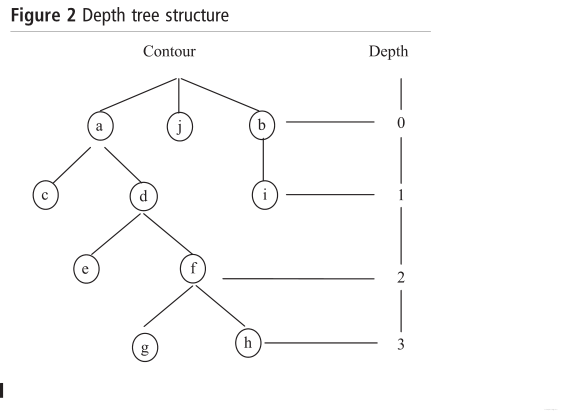图2
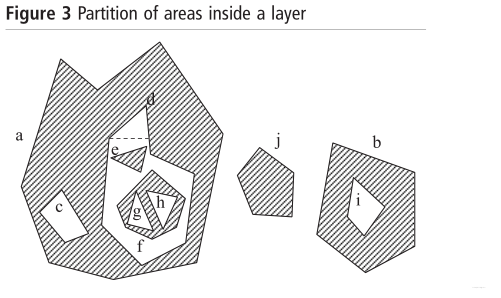图3

图2、3引用自 Y. Yang,et al.Equidistant path generation for improving scanning efficiency in layered manufacturing[J].Rapid Prototyping Journa,2002,Volume 8 · Number 1:30-37.

4.内循环和外循环：循环数是偶数，则是外循环，否则是内循环。如图2、3所示。

5.链的方向：链的左侧为实体时，此时链的前进方向为正方向。
   显然，对于外循环，逆时针为正方向；对于内循环，顺时针为正方向。

1.2 域分区

（文章中并没有提及怎样进行分区处理，需要后续进行学习）
这是生成算法的预处理步骤，需要识别出切片层的实体部分（如图3中的阴影部分），这些部分将被填充，可以视为深度树中偶数的循环和其下一层循环之间的部分。

1.3 偏移量的生成

（文章中只有简单多边形的偏移量生成方法，没有提及曲线偏移量的生成方法，且在SLM过程中，也许会为了提高加工质量而更改加工参数，可能需要变距、变激光功率）

该算法的主要思想是等距离偏移轮廓。
链的直线可以用以下式子表示：

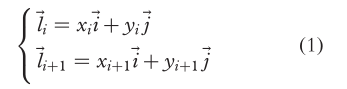
相邻两条边产生外偏移量的直线时会产生一个交点，如图4所示，该交点的方程为：

内偏移的交点方程为：

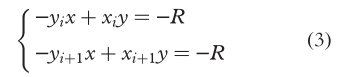
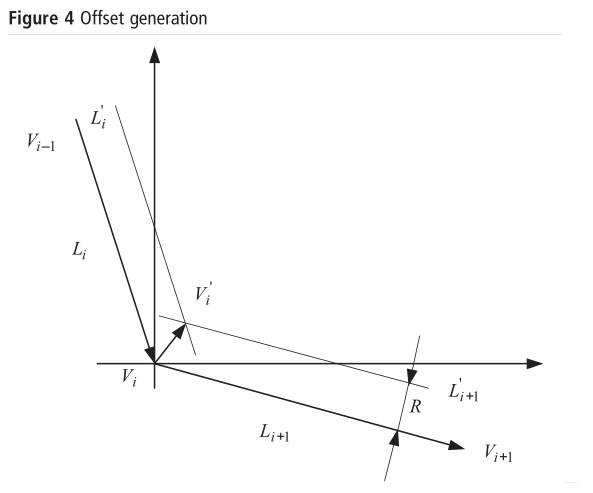图4

图4引用自 Y. Yang,et al.Equidistant path generation for improving scanning efficiency in layered manufacturing[J].Rapid Prototyping Journa,2002,Volume 8 · Number 1:30-37.

求解方程可得到交点坐标：

将得到的所有交点按顺序相连，可得到偏移的轮廓。

1.4 自交问题

如图5所示，某条轮廓偏移线可能出现自交的情况。
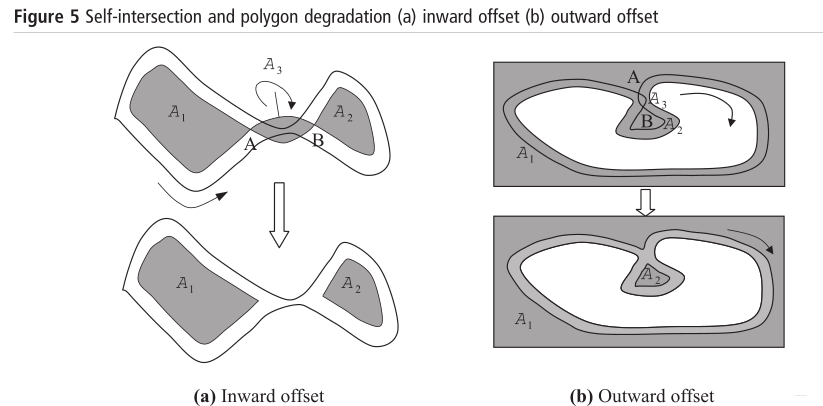图5

图5引用自 Y. Yang,et al.Equidistant path generation for improving scanning efficiency in layered manufacturing[J].Rapid Prototyping Journa,2002,Volume 8 · Number 1:30-37.

可以检查某条偏移线的交点，看是否发生了非相邻边相交的情况，并记录下来。
当发生自交时，说明这条偏移线中有小于最小可制造尺寸的位置，应当划分为多条闭合曲线，如图5所示。
用记录下来的交点之外的链构成的简单多边形循环当作新的独立的循环，交点之间的部分丢弃。

1.5 尖角

（感觉用处不大，没有细研究）
有一些尖角特征太细小了就是打印不出来，而且还会影响到下一次轮廓偏移，需要处理成比较平滑的轮廓。如图6所示。
图6

图6引用自 Y. Yang,et al.Equidistant path generation for improving scanning efficiency in layered manufacturing[J].Rapid Prototyping Journa,2002,Volume 8 · Number 1:30-37.

1.6 外部轮廓和内部轮廓相交

如图7所示，有时会出现外部轮廓和内部轮廓相交的情况。
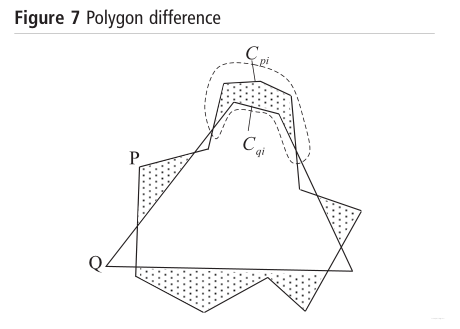图7

图7引用自 Y. Yang,et al.Equidistant path generation for improving scanning efficiency in layered manufacturing[J].Rapid Prototyping Journa,2002,Volume 8 · Number 1:30-37.

这两条循环将平面分为许多小区域，其中只有逆时针方向的封闭链是实体区域的边界，将这些链作为新的循环，最终可以形成如图8所示的效果。
图8

图8引用自 Y. Yang,et al.Equidistant path generation for improving scanning efficiency in layered manufacturing[J].Rapid Prototyping Journa,2002,Volume 8 · Number 1:30-37.

1.7 空隙

这种方法会产生空隙，采用不同层之间不同的偏移量来解决。
（在slm中，相邻轨道之间有一部分重叠，所以空隙问题可能并不明显，并且这篇论文中对于空隙处理的方式太落后了，后续需要学习新的方法）

1.8 连续运动

在材料喷射类方法中，喷嘴路径需要连续。
（但是在粉末床类的技术中不需要，所以这部分问题不是问题）

二.评估

2.1 总路径长度

（这篇论文中材料喷射的喷头速度恒定，所以计算方法并不适用）
结论：由于这种算法有路径重叠的问题，所以总路径比平行扫描方式略长。但是由于本方法的曲率和拐角较少，不需要喷嘴减速到静止再加速运动，整体速度略快于平行扫描方式。

2.2 表面质量

由于平行扫描方式的所有扫描末端都集中在表面部分，导致表面质量要比本方法差。

三.我的问题

1.粉末床类的工艺和材料喷射类工艺有相似之处，也有不同之处，那么在算法上需要怎样改进以适应粉末床类的工艺？
2.每种规划路径都需要有一些优化目标，我的优化目标是什么呢？