上一章分析基本神经网络以及怎么训练网络过程。里面有用到提到BP (反向传播的求解)
1)BP 其实是一种思想
首先我们看一个计算式子
e
=
(
a
+
b
)
∗
(
b
+
1
)的
图模型:如下左图所示,
其中,
c
,
d
表示中间结果,边的方向表示一个结点是另一个结点的输入。
假设输入变量
a
=
2
,
b
=
1
时,图中各结点的偏导计算结果如下:




对比两张图,发现第二张图都已经求出离e对各变量的导数,而第一张图,如果需要求出变量是需要重复步骤。BP算法只是减少了计算,并不是说正向传播不能解决问题。
2)为啥需要BP
需要BP的原因是需要训练参数w,怎么求w
3)代价函数
我们希望对于输入x ,产生的y尽可能与期望的y相等。或者说我们希望下面的表达式最小。
、
求解最小问题就需要求导。
4)完整BP过程
Calculus on Computational Graphs: Backpropagation
http://colah.github.io/posts/2015-08-Backprop/
5)基于sigmoid的BP过程
对于目标函数:代价函数
需要求解,如下η表示步长,由用户设定,右边wji表示前一次的参数,初始值为0,

发现是不是都是关于E对w的求导。符号第一点的要求。
定义变量&4,,,&8
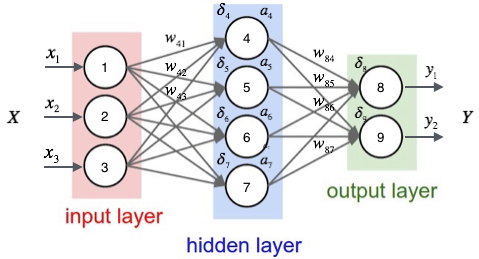
观察上图,我们发现权重
wji仅能通过
影响节点j
的输入值影响网络的其它部分(
前面只能影响后面),设
netj是节点
j
的加权输入,即
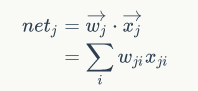
链式求导
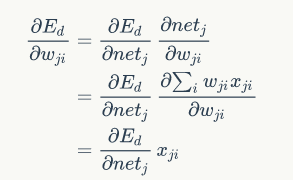
1)
输出层权值训练
有:
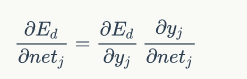
分别求解:

则:
![]()

有:
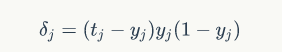
得到输出层的方程
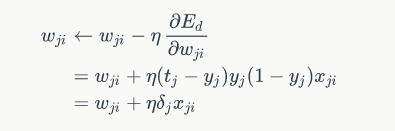
2)隐藏层权值训练

隐含层:
![]()
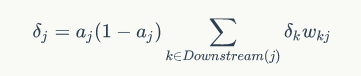
3)结论:
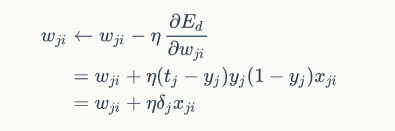
当输出层时:
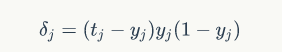
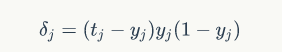
当隐含层时:
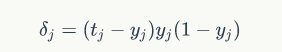
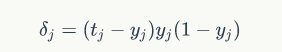





 本文深入解析了反向传播(BP)算法的基本原理及其在神经网络训练中的应用。从计算图模型出发,对比了正向与反向微分算法,阐述了BP如何减少计算量并高效求解参数梯度。此外,还详细介绍了基于sigmoid激活函数的BP过程。
本文深入解析了反向传播(BP)算法的基本原理及其在神经网络训练中的应用。从计算图模型出发,对比了正向与反向微分算法,阐述了BP如何减少计算量并高效求解参数梯度。此外,还详细介绍了基于sigmoid激活函数的BP过程。


















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








