蒙特卡罗仿真（2）：醉汉的随机漫步仿真示例（Python实现）

笨牛慢耕

已于 2023-02-12 11:13:12 修改

阅读量5.9k

点赞数 5

分类专栏：人工智能文章标签： python 蒙特卡罗方法随机仿真随机漫游随机游走定理

于 2022-03-28 16:14:30 首次发布

本文链接：https://blog.csdn.net/chenxy_bwave/article/details/123747245

版权

人工智能专栏收录该内容

58 篇文章 33 订阅

订阅专栏

1. 前言

上一篇（蒙特卡罗仿真（1）：入门求生指南（Python实例））通过几个简单的实例介绍蒙特卡罗仿真的一些基础知识。这一篇我们来看一个稍微复杂一些的有趣例子，随机游走问题，通俗的说法是醉汉的随机漫步问题。醉汉可能在一维直线上做前后随机漫步，也可能在二维平面上做随机漫步，也可以（在想象的世界里你无所不能）在更高维的空间中做随机漫步。。。当然在三维情况下的讨论通常主角换成喝醉的小鸟，毕竟人是难以自由地进行三维运动的。但是另一方面，小鸟又为什么会喝醉呢？。。。不过这些并不重要，只是为了是所研究的问题对象变得更形象一些的调味元素而已。

好了，言归正传。本文以下以二维随机漫步为例。

2. 为什么要做蒙特卡罗仿真？

在问题中，醉汉从坐标原点（0，0）出发，每一步他可能向东南西北四个方向随机选择一个方向向前走一步（一个坐标单位）。在第一步之后他的位置有4种可能性，如下图所示（图来源于【1】MIT6_0002F16_lec5）

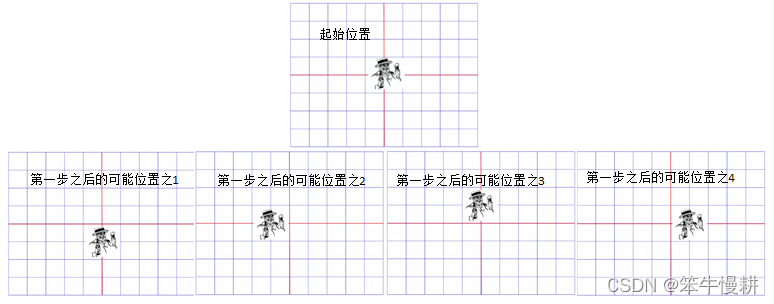
watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA56yo54mb5oWi6ICV,size_20,color_FFFFFF,t_70,g_se,x_16

以后每走一步都会四种可能性，因此经过k步之后，他可能的位置有 $gif.latex?4%5Ek$ 种可能性。。。当然，这是不准确的。因为只谈论位置的话，他有可能重复回到某个位置，因此k步之后，他可能的位置可能性数会小于 $gif.latex?4%5Ek$ 种可能性。但是如果我们谈论从第一步开始之后的轨迹的话，则的确会有 $gif.latex?4%5Ek$ 种可能性。

由于可能的轨迹数随着步数呈指数增长，所以关注某一次实验中中k步之后醉汉位置在哪儿可能价值不大。我们可能更关心的是，在k步之后醉汉离原点的距离的预期均值是多少，呈什么样的分布，最远到过多远，出发以后有没有回到过原点，等等等等。显然这样的问题我们无法通过计算得到一个确定性的值，我们有两种选择：

基于随机过程理论进行理论解析
基于蒙特卡洛仿真得到近似结果

事实上对于绝大多数人来说，只有一种选择，那就是蒙特卡罗仿真法，只要会编程就可以做得到。第一种选择需要相当程度的数学能力（特别是随机过程理论方面）。

3. 第一个仿真程序

import numpy as np
import matplotlib.pyplot as plt

steps = np.array([(1,0), (0,-1), (-1,0),(0,1)]) # East, South, West, North
print(steps)
numSteps = 100000
locs      = np.zeros((numSteps,2))
for k in range(1,numSteps):
    step = steps[np.random.choice(np.arange(4))]
    locs[k]  = locs[k-1] + step
    
dist = np.sqrt(locs[:,0]**2 + locs[:,1]**2)            
dist_min = np.min(dist)
dist_max = np.max(dist)
origins = [] 
for k in range(numSteps):
    if locs[k,0]==0 and locs[k,1]==0:
        origins.append(k)
print('numSteps = {0}, final loc = {1}, dist = {2}, dist_min = {3}, dist_max = {4}'.format(numSteps,locs[-1],dist[-1], dist_min, dist_max))
print(origins)

plt.plot(locs[:,0],locs[:,1])
plt.title('random walks: {0} steps'.format(numSteps))
plt.show()

运行以上脚本会得到以下结果和图（表示醉汉的运动轨迹）

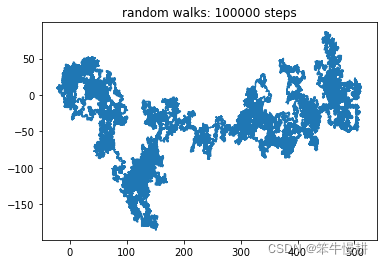
watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA56yo54mb5oWi6ICV,size_13,color_FFFFFF,t_70,g_se,x_16

numSteps = 100000, final loc = [-151. 474.], dist = 497.4706021464987, dist_min = 0.0, dist_max = 516.1395160225576
Time-stpes returning to the origins: [2, 54]

以上结果中包括最终位置和（离原点的）距离，到过的最远距离，以及有两次回到过原点。

重复执行以上脚本会得到不同的结果。改变numSteps也会得到不相同的结果。

但是，这样手动地一次次地执行效率很低下，也很难看出我们所关心的事情，比如说，在k步之后醉汉离原点的距离的预期均值、方差及其分布，等等。首先，这个需要执行很多次实验才能得到有足够统计意义的数据，其次还需要对所收集的实验数据进行统计分析。

因此，接下来我们需要对仿真程序进行封装，以便于能够自动地进行批量的仿真，并自动地对实验结果进行统计分析。

4. 仿真封装及批量仿真

考虑把核心的仿真处理封装到一个函数random_walk()中，每次调用该函数执行一次numSteps步数的仿真（借用强化学习中的术语，或可称之为一个episode，回合），返回该回合中最终位置和距离，在漫步过程中到过的最远距离和最近距离。重复numRuns次random_walk(numSteps)的调用构成一次仿真，这个进一步封装成multiple_walks()函数。

# -*- coding: utf-8 -*-
"""
Created on Sat Mar 26 11:41:18 2022

@author: Chenxy
"""
import numpy as np
import matplotlib.pyplot as plt
import time

steps = np.array([(1,0), (0,-1), (-1,0),(0,1)]) # East, South, West, North

def random_walk(numSteps):    
    locs      = np.zeros((numSteps,2))
    return2start = False
    dist_max  = 0
    for k in range(1,numSteps):
        step = steps[np.random.choice(np.arange(4))]
        locs[k]  = locs[k-1] + step

    dist     = np.sqrt(locs[:,0]**2 + locs[:,1]**2)
    dist_max = np.max(dist)
    return2start = np.min(dist[1:]) == 0 
    final_loc  = locs[-1]
    final_dist = dist[-1]
    return return2start, dist_max, final_loc,final_dist

def multiple_walks(numSteps, numRuns):    

    return2start = np.zeros((numRuns,))
    dist_max     = np.zeros((numRuns,))
    final_loc    = np.zeros((numRuns,2))
    final_dist   = np.zeros((numRuns,))

    tstart =time.time()
    for k in range(numRuns):
        return2start[k], dist_max[k], final_loc[k,:],final_dist[k] = random_walk(numSteps)        
        if k%1000==0: 
            print('k={0}'.format(k))
    tstop  =time.time()
    print('Time cost for {0} simulation with numSteps={1} is {2:6.2f}(sec)'.format(numRuns,numSteps,tstop-tstart))
    fail_ratio_to_return_start = 1-np.sum(return2start)/numRuns
    print('failure ratio to return to start point = {0:4.2f}%'.format(fail_ratio_to_return_start*100))
    print('dist_max: mean={0}, std={1}'.format(np.mean(dist_max),np.std(dist_max)))
    print('final_dist: mean={0}, std={1}'.format(np.mean(final_dist),np.std(final_dist)))

    # Visualize the simulation result
    fig,ax = plt.subplots(1,2,figsize=(16,8))
    ax[0].hist(dist_max,bins=50, density=True)
    ax[0].set_title('dist_max histogram, with numSteps={0}'.format(numSteps))
    ax[1].hist(final_dist,bins=50, density=True)
    ax[1].set_title('final_dist histogram, with numSteps={0}'.format(numSteps))

    fig,ax = plt.subplots()
    ax.scatter(final_loc[:,0],final_loc[:,1])
    ax.set_title('final_loc scatter plot, with numSteps={0}'.format(numSteps))

基于以上实现执行批量仿真回答以下几个问题：

醉汉在numSteps步数的漫步过程有没有回到过起点？
醉汉到过的最远距离的分布及其均值方差等
醉汉最终位置的分布
醉汉最终位置的离起点距离的分布及其均值方差等

然后以不同numSteps执行以上仿真，看看以上统计特性是如何受numSteps影响的。最后一个因为时间太长所以numRuns设的比较小。

multiple_walks(numSteps=100    ,numRuns=10000)    
multiple_walks(numSteps=1000   ,numRuns=10000) 
multiple_walks(numSteps=10000  ,numRuns=1000)

仿真结果如下：

#####################################

Time cost for 10000 simulation with numSteps=100 is 22.67(sec)
failure ratio to return to start point = 40.94%
dist_max: mean=11.295139424500979, std=3.896540180863491
final_dist: mean=8.782640091678228, std=4.585633328128867

#####################################

Time cost for 10000 simulation with numSteps=1000 is 227.73(sec)
failure ratio to return to start point = 32.49%
dist_max: mean=37.01111678401759, std=12.613509995231741
final_dist: mean=28.322730894706165, std=14.866718355644494

#####################################

Time cost for 1000 simulation with numSteps=10000 is 217.35(sec)
failure ratio to return to start point = 23.00%
dist_max: mean=118.47491429371055, std=40.00567063677272
final_dist: mean=90.00791969357836, std=47.18782038232269

其中，numSteps=10000时的最终/最远距离的直方图，以及最终停留位置的散点图如下所示：

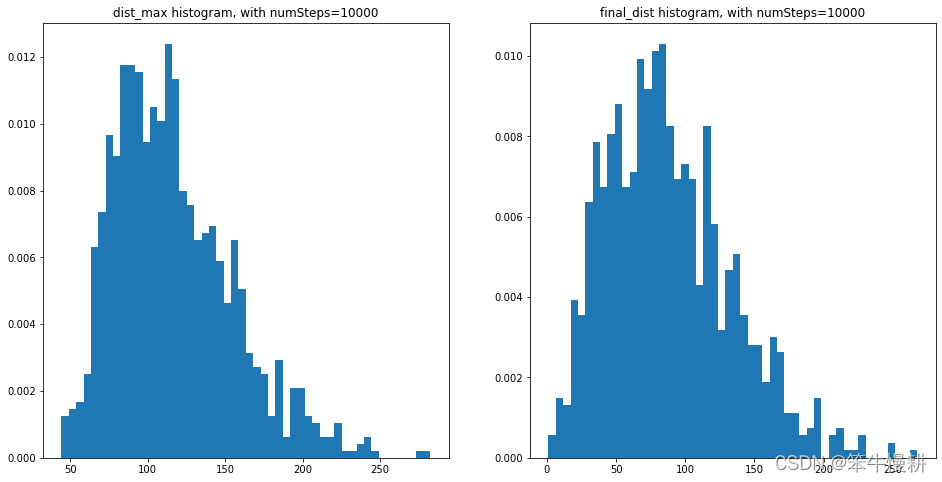
watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA56yo54mb5oWi6ICV,size_20,color_FFFFFF,t_70,g_se,x_16

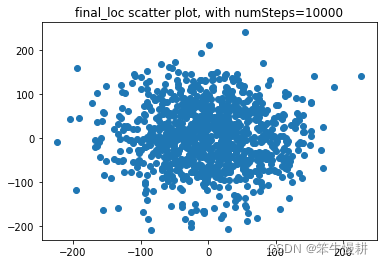
watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA56yo54mb5oWi6ICV,size_13,color_FFFFFF,t_70,g_se,x_16

【Observation】

(1) 醉汉有一定的概率回不了家
(2) 到过的最远距离与最终距离的均值和方差有差异
(3) 最远距离与最终距离的均值和方差都大致与sqrt(numSteps)相当

如何解释这些结果呢？这些结果有什么必然性吗？仿真可以提供这些结果（当然前提条件是确保仿真本身是正确的），仿真本身回答不了这些问题，但是可以为理论分析提供线索和方向。但是，当一个仿真模型通过实验结果与理论分析得到确认后，就可以基于此进行预测，充当深入到理论分析无法或者至少难以涉足的“无人区”去探索的有力工具了。