Matlab/Simulink：动态系统模型的表示及仿真分析基础

笨牛慢耕

已于 2022-06-13 21:32:43 修改

阅读量7.1k

点赞数 4

分类专栏： Matlab 文章标签： matlab 开发语言 simulink 动态系统

于 2022-06-07 23:10:08 首次发布

本文链接：https://blog.csdn.net/chenxy_bwave/article/details/125169429

版权

Matlab 专栏收录该内容

23 篇文章 36 订阅

订阅专栏

1. 前言

本文对Matlab/Simulink建模中常见的动态系统及其表示进行概要性的介绍。

按照动态系统是否有记忆可以分为无记忆系统和有记忆系统。

按照动态系统在时间域是连续的还是离散的可以分为连续时间系统（简称连续系统）和离散时间系统（简称离散系统）。如果其中既包含连续动态子系统也包含离散动态子系统的话，则可以称为混合时间系统（简称混合系统）。

按照系统是否满足线性性可以分为线性系统和非线性系统。

按照系统的行为是随时间变化的还是不随时间变化的可以分为时变系统和时不变系统（或定常系统）。

本文的介绍着重点在于线性时不变系统（LTI：Linear Time-Invariant system）。

无记忆系统的分析和建模比较简单（不管是连续还是离散，线性还是非线性），通常我们又把无记忆系统称为简单系统。

动态系统的通常的研究对象都是指有记忆系统。以下所讨论的除了无记忆系统以外，其它的均指有记忆系统。非线性系统通常都很难进行分析（一般来说常用的手段是先进行线性化近似转换为线性系统后再进行研究）。

2. 线性性

一个变换如果满足如下性质，则称之为线性变换，这个性质称之为线性性，其中包含齐次性和叠加性两个性质：

$T(a \cdot x + b \cdot y) = a \cdot T(x) + b \cdot T(y)$

3. 无记忆系统

无记忆系统是指：

(1) 系统某一时刻的输出直接且唯一依赖于该时刻的输入量
(3) 系统中不存在输入的状态量，所谓的状态量是指系统输入的微分项（即输入的导数项）（对于连续系统）或者说差分项（对于离散系统）

设简单系统的输入为x，系统输出为y，x可以具有不同的物理含义。对于任何系统，都可以将它视为对输入变量x的某种变换，因此可以用T [ ]表示任意一个系统，即 $y = T[x]$ 。对于简单系统，系统输出变量y仅与x的当前值相关，从数学的角度来看，y是x的一个函数，给出一个x值，便有一个y值与之对应。

注意，x本身也是时间的函数，当时间发生变化，输入x和输出y自然是发生变化。但是这个并不意味着这个系统是时变系统。时变系统是指变换T本身是随着时间t的变化而变化。一般来说，时变系统会记作 $y(t) = T_t(x(t))$ ，用以表示变换T是依赖于时间t的（相反，其实变换T本身是不依赖于x的）。

3.1 描述方式

一般来讲，无记忆系统都可以采用代数方程与逻辑结构相结合的方式进行描述。

【代数方程】

采用数学方程对简单系统进行描述，可以很容易由系统输入求出系统输出，并且由此可方便地对系统进行定量分析。

【逻辑结构】

一般来说，系统输入都有一定的范围。对于不同范围的输入，系统输出与输入之间遵从不同的关系。由系统的逻辑结构可以很容易了解系统的基本概况。

3.2 无记忆系统例子

例1. 考虑如下的一个系统：

$y = \begin{cases} & t^2 \text{ if } 0 \leq t <1 \\ & t^{\frac{1}{2}}\text{ if } t \geq 1 \end{cases}$

其中t为系统的输入变量，也即时间变量，y为系统的输出变量。很显然，此系统是一个时变无记忆系统的条件。系统输出仅由系统当前时刻的输入（即当前时刻自身）决定。但是变换方式在t=1前后发生了变化。这个系统可以用matlab建模仿真如下：

% example1.m文件
t=0:0.1:10;     % 设定系统输入范围与仿真步长
leng=length(t); % 计算系统输入序列长度
for i=1:leng    % 计算系统输出序列
    if t(i)<=1  % 逻辑判断
        y(i)=t(i).^2;
    else
        y(i)=sqrt(t(i));
    end
end
plot(t,y);grid; % 绘制系统仿真结果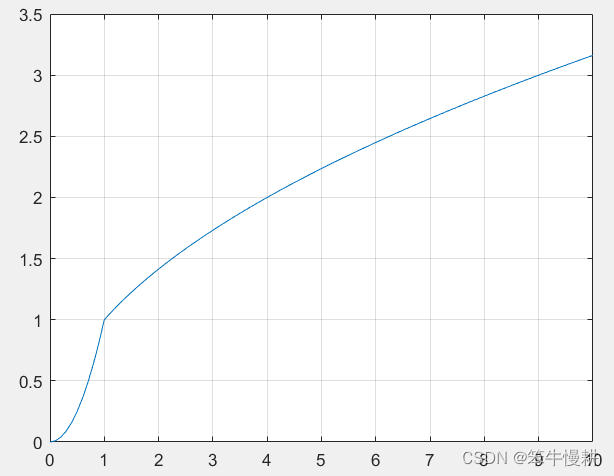

容易验证，以上这个例子不是线性系统。

4. 线性时不变连续系统

4.1 基本概念

连续系统是指系统输出在时间上连续变化，而非仅在离散的时刻采样取值。连续系统满足以下条件：

(1) 系统的状态和输出在时间域连续变化
(2) 对系统的数学描述来说，存在系统输入或输出的微分项（导数项），即系统以微分方程的形式进行描述

连续系统通用数学描述为： $y(t) = f_t(x(t))$ 。系统的输入变量与输出变量既可以是标量（单输入单输出系统），也可以是向量（多输入多输出系统）。而且在系统的数学描述中含有系统输入或输出的导数。连续系统也可以分解为状态方程和输出方程相结合的描述方式，称为状态空间模型，如下所示：

$\begin{align} \dot{s} &= f(s(t),x(t),t) \\ y &= g(s(t),x(t),t) \end{align}$

这里x(t)表示系统的输入，s(t)表示系统的状态。第1个方程称为状态方程，第2个方程称为输出方程。

例2：考虑以下动态系统例：

$y(t) = u(t) + \dot{u(t)}, \quad u(t) = t + sin t, t \geq 0$

$y(t) = t + sin t + 1 + cost = t + sin t + cost + 1, t \geq 0$

这个系统可以用matlab建模仿真如下：

close all; clear; clc

t    = 0:0.1:5;     %系统仿真范围，时间间隔为0.1 s
ut   = t+sin(t);    %系统输入变量
utdot= 1+cos(t);    %系统输入变量的导数
yt   = ut+utdot;    %系统输出
plot(t,yt);grid;    %绘制系统输出曲线

4.2 线性时不变连续系统

如果一个连续系统的数学方程所表示的变换满足线性性，且该变换不随时间变化而变化（体现为微分方程中各项系数为常数），则该连续系统称为线性时不变连续系统。容易验证例2中所示的连续系统是一个线性连续系统（注意，是指关于u线性，而不是关于t线性）。

线性时不变连续系统可以用以下四种方式进行描述：

微分方程
传递函数
零极点模型
状态空间模型

4.2.1 微分方程

线性时不变连续系统的微分方程通用形式为：

$a_0 y^{n}(t) + a_1 y^{n-1}(t) + \cdots + a_{n-1} y^1(t) + a_{n} y(t) \\= b_0 x^{m}(t) + b_1 x^{m-1}(t) + \cdots + b_{m-1} x^1(t) + b_{m} x(t), \quad n \geq m$

其中y(t)表示系统输出，x(t)表示系统输入。

$u^{(k)}(t)$ 表示u(t)的k阶导数。

$n \geq m$ 的约束不是必须的，但是 $n<m$ 的情况总是可以简化为一个纯时延系统与一个满足 $n \geq m$ 的系统的串联，因此通常只需要研究 $n\geq m$ 的情况即可。事实上，可以更进一步约束为 $n>m$ ，因为 $n = m$ 意味着系统中包含着一条从输入到输出的无记忆路径，可以单独提取出来考虑。

4.2.2 传递函数

线性连续系统的传递函数模型与零极点模型是基于连续信号的拉氏（拉普拉斯）变换来实现的。拉氏变换满足如下两个性质：

(1) 线性性。即对于连续信号 $u_1(t)$ 和 $u_2(t)$ ，设它们的拉氏变换分别为 $L(u_1(t))$ 与 $L(u_2(t))$ ，则拉氏变换的线性性是指拉氏变换满足下面的关系：

$L(a \cdot u_1(t) + b \cdot u_2(t)) = a \cdot L( u_1(t)) + b \cdot L( u_2(t))$

(2) 设连续信号 $u(t)$ 的拉氏变换为 $U(s)$ ，则 $\dot{u}(t)$ 的拉氏变换为 $sU(s)$ ， $\ddot{u}(t)$ 的拉氏变换为 $s^2U(s)$ 。更高阶的导数的拉氏变换以此类推。

在零初始条件下，输出量与输入量的拉普拉斯变换之比就是这个系统的传递函数。对一个线性连续系统的微分方程的两边同时取拉氏变换，然后经过数学整理便可以得到该系统的传递函数（transfer function，也称传输函数）。

例3： $u(t) = m \ddot{y} (t) + b \dot{y} (t) + ky(t)$

对两边取拉氏变换然后整理为分式可得： $\frac{Y(s)}{U(s)} = \frac{1}{m s^2 + b s + k}$ ，此即为该系统的传递函数。

一般来说，线性连续系统的传递函数的通用形式如下所示：

$H(s) = \frac{Y(s)}{X(s)}= \frac{\sum\limits_{k=0}\limits^{k=m}b_k s^{m-k}}{\sum\limits_{l=0}\limits^{l=n}a_l s^{n-l}}$

如果传递函数分母中的s的最高次项为n，则称该系统为n阶系统。

4.2.3 零极点模型

将传递函数的分子和分母分别因式分解处理，便可得到线性时不变连续系统的零极点模型：

$\begin{align} H(s) &= K\frac{(s-z_1)(s-z_2)\cdots(s-z_m)}{(s-p_1)(s-p_2)\cdots(s-p_n)} \\ &= K\frac{\prod\limits_{i=1}\limits^{i=m}(s-z_i)}{\prod\limits_{j=1}\limits^{j=n}(s-p_j)} \end{align}$

其中 $z_i$ 为线性连续系统的零点， $p_j$ 为系统的极点， $K$ 为系统的增益。

4.2.4 状态空间模型

线性连续系统的另外一种模型为状态空间模型。对于线性时不变连续系统，使用其微分方程很容易推导出系统的状态空间模型。这里给出线性连续系统用状态空间模型进行描述的一般方式：

$\left\{\begin{matrix} \dot{x}(t) = A x(t) + B u(t) \\ y(t) = C x(t) + D u(t) \end{matrix}\right.$

其中，第一个方程是状态方程，它其实是一阶微分方程（组）；第二个方程是所谓的输出方程。

其中， $x(t)$ 为线性连续系统的状态变量， $u(t)$ 和 $y(t)$ 分别为系统的输入与输出变量，可以为标量，也可以为向量。A、B、C和D均为常数矩阵。

4.3 Matlab中的线性时不变连续系统表示

这里以简单的2阶系统为例说明。

在Matlab中，传递函数表示为num=[n0,n1]; den=[d0,d1,d2]; 其中num表示传递函数的分子系数向量，den为分母系数向量。注意，分子系数n0,n1和分母系数d0,d1,d2是按照传递函数的分子和分母中的s的降幂排列的系数（请与上一节所示的传递函数对比）。

在Matlab中，零极点模型表示为gain=k; zeros=z1; poles=[p1,p2]; 其中gain表示系统增益，zeros表示系统零点，poles表示系统极点。

在Matlab中，状态空间模型则直接以上节所示的四个矩阵A、B、C和D表示。

比如说，有一个线性连续系统的传递函数为 $H(s) = \frac{0.5s+1}{s^2+0.5s+1}$ ，则可以用一下matlab脚本求它的频域响应如下：

num = [0.5, 1];
den = [1, 0.5, 1];
freqs(num, den); title('Frequence response');

4.4 各种表示形式之间的转换

Matlab提供了在三种形式之间进行转换的工具函数，如下所示：

[zeros,poles,k]= tf2zp(num,den);
[num,den] = zp2tf(zeros,poles,k)；
[zeros,poles,k]= ss2zp(A,B,C,D);
[A,B,C,D] = zp2ss(zeros,poles,k)
[num,den] = ss2tf(A,B,C,D)
[A,B,C,D] = tf2ss(num,den)

举例如下：

num = [0.5, 1];
den = [1, 0.5, 1];
[zeros,poles,k]= tf2zp(num,den)
[num,den]      = zp2tf(zeros,poles,k)
[A,B,C,D]      = tf2ss(num,den)

运行可得结果如下：

zeros = -2

poles = -0.2500 + 0.9682i
-0.2500 - 0.9682i
k = 0.5000

num = 0 0.5000 1.0000

den = 1.0000 0.5000 1.0000

A = -0.5000 -1.0000
1.0000 0

B = 1
0

C = 0.5000 1.0000

D = 0

4. 线性时不变离散系统

4.1 基本概念

所谓离散系统，是指系统的输入与输出仅在均匀间隔的离散时间上取值，在这些离散时间间隔之间输入和输出都没有定义，或者说不关心。这些离散时间点称为采样时刻，采样时刻之间的间隔即为采样周期。除此以外，离散系统与连续系统的性质相似。

离散系统的数学描述可以表示为如下差分方程：

$y(k) + a_1 y(k-1) + a_2 y(k-2) + ... + a_n y(k-n) \\ = b_0 x(k) + b_1 x(k-1) + ... + b_m x(k-m)$

可以简写为：

$y(k) = \sum\limits_{i=0}\limits^{i=m}b_i x(k-i) - \sum\limits_{j=1}\limits^{j=n}a_j y(k-j)$

与前述连续系统相似的是，通常我们假设 (n > m)，此外还默认 $a_n \neq 0$ ，以上方程称为n阶差分方程。

例4，考虑如下的离散系统： $y(n) = u^2(n) + 2u(n-1) + 3 y(n-1)$ ，其中系统的初始状态为y(0)=3，系统输入为x(n)，则系统在时刻0，1，2……的输出分别为:

$\begin{align} y(0) &= 3 \\ y(1) &= u^2(1) + 2u(0) +3 y(0) = 4 + 0 + 9 = 13 \\ y(2) &= u^(2) + 2u(1) + 3y(1) = 16 + 4 + 39 = 59 \end{align}$

这个系统可以用matlab建模仿真如下：

y(1)=3; % 表示离散系统初始状态为3
        % 由于MATLAB中数组下标从1开始，这里y(1)相当于上文中的y(0)=3，下同
u(1)=0; % 表示离散系统初始输入为0
for i=2:11    % 设定离散系统输入范围为时刻0到时刻10
    u(i)=2*i; % 离散系统输入向量
    y(i)=u(i).^2+2*u(i-1)+3*y(i-1); % 离散系统输出向量
end
figure; plot(u,y,'k*-');grid; % 绘制系统仿真结果

以上例子中并没有指定离散系统的采样周期。在实际的系统中，必须指定系统的采样时间，
只有这样才能获得离散系统真正的动态性能。当然，也可以理解为采样周期为单位时间1。

4.2 线性时不变离散系统

同样的，如果一个离散系统的数学方程所表示的变换满足线性性，则该离散系统称为线性离散系统。当差分方程中的系数都为常数时，则该系统为线性时不变离散系统。

与线性离散系统表示相似，线性离散系统也有以下四种描述方式：

差分方程（对应于连续系统的微分方程）
传递函数
零极点模型
状态空间模型

只不过线性连续系统的传递函数模型和零极点模型是基于拉氏变换，而线性离散系统的传递函数模型和零极点模型则是基于Z变换。与拉氏变换一样，Z变换也满足以下两条性质：

(1) 线性性

(2) 设离散信号 $u(n)$ 的z变换为 $U(z)$ ，则 $u(n-1)$ 的拉氏变换为 $z^{-1}U(z)$ ， $u(n-2)$ 的z变换为 $z^{-2}U(z)$ 。余者依此类推。

4.2.1 传递函数

对一个线性离散系统的基本数学方程的两边同时取z变换，然后经过数学整理便可以得到该系统的传递函数（transfer function，也称传输函数）。

$y(k) = \sum\limits_{i=0}\limits^{i=m}b_i x(k-i) - \sum\limits_{j=1}\limits^{j=n}a_i y(k-i)$

对该式两边取z变换可得：

$H(z) = \frac{Y(z)}{X(z)} = \frac{\sum\limits_{i=0}\limits^{i=m}b_i z^{-i} }{\sum\limits_{j=0}\limits^{j=n}a_j z^{-j})} , \ a_0 = 1$

4.2.2 零极点模型

与线性连续系统相同，将传递函数的分子和分母分别进行因式分解可以得到对应的零极点描述：

$H(z) = \frac{Y(z)}{X(z)} = \frac{(z^{-1}-z_1^{-1})(z^{-1}-z_2^{-1})\cdots (z^{-1}-z_m^{-1})}{(z^{-1}-p_1^{-1})(z^{-1}-p_2^{-1})\cdots (z^{-1}-p_n^{-1})}$

眼尖得小伙伴也许已经注意到了线性离散系统的传递函数模型、零极点模型中出现的是z的负指数幂，这个是由于z变换的延迟属性所致。后文所说的tf2zp与tf2zpk的细微差异其实也是源于此。关于离散系统和连续系统的处理的异同点等将另文讨论，此处暂且不表，知道有这么个差异即可。

4.2.3 状态空间模型

同样由线性离散系统的基本数学方程也可以推导得出对应的状态空间模型：

$\begin{align} x(n+1) &=Ax(n)+Bu(n) \\ y(n)&=Cx(n)+Du(n) \end{align}$

其中，第一个方程是状态方程，它其实是一阶差分方程（组）；第二个方程是输出方程。

4.4 Matlab中的线性离散系统表示

与线性连续系统相同，线性离散系统在Matlab中有以下三种表示形式（以下以2阶系统为例说明）：
在Matlab中，系统的传递函数表示为num=[n0 n1 n2]; den=[d0 d1]；其中num表示传递函数的分子系数向量，den为分母系数向量。注意，分子系数n0,n1和分母系数d0,d1,d2是按照传递函数的分子和分母中的s的降阶排列的系数（请与上一节所示的传递函数对比）。

在Matlab中，零极点模型表示为gain=k; zeros=[z1,z2]; poles=[0,p1]; 其中gain表示系统增益，zeros表示系统零点，poles表示系统极点。

在Matlab中，状态空间模型则直接以上节所示的四个矩阵A、B、C和D表示。

例5，考虑线性离散系统： $\frac{Y(z)}{U(z)} = \frac{2z^2-z-5}{z^3+3z^2+6z+2}$ ，则可以用一下matlab脚本求它的频域响应如下：

num=[2, -1, -5];
den=[1 3 6 2];
figure; freqz(num,den);
grid;

4.5 各种表示形式之间的转换

与线性连续系统相似，Matlab也为线性离散系统提供了在三种表示形式之间进行转换的工具函数，如下所示：

[zeros,poles,k]= tf2zpk(num,den), or tf2zp(num,den);
[num,den] = zp2tf(zeros,poles,k)；
[zeros,poles,k]= ss2zp(A,B,C,D);
[A,B,C,D] = zp2ss(zeros,poles,k)
[num,den] = ss2tf(A,B,C,D)
[A,B,C,D] = tf2ss(num,den)

注意，tf2zp和tf2zpk存在细微的差异，从以下例子中也可以看出。这个的原因以后补充说明。其它5个函数没有这个带或不带k的函数版本的区分。

例6，仍考虑例5中的系统，不同表示形式之间的变换如下：

num=[2, -1, -5];
den=[1 3 6 2];
[zeros,poles,k]= tf2zp(num,den)
[zeros,poles,k]= tf2zpk(num,den)
[num,den]      = zp2tf(zeros,poles,k)
[A,B,C,D]      = tf2ss(num,den)

zeros =

1.8508
-1.3508

poles =

-1.2980 + 1.8073i
-1.2980 - 1.8073i
-0.4039 + 0.0000i

k = 2

zeros =

0
1.8508
-1.3508

poles =

-1.2980 + 1.8073i
-1.2980 - 1.8073i
-0.4039 + 0.0000i

k = 2

num =

2.0000 -1.0000 -5.0000 0

den =

1.0000 3.0000 6.0000 2.0000

A =

-3.0000 -6.0000 -2.0000
1.0000 0 0
0 1.0000 0

B =

1
0
0

C =

-7.0000 -17.0000 -4.0000

D =

2

5. 混合系统

混合系统是由连续子系统和离散子系统共同构成的，因此混合系统的数学描述可以由不同类型系统描述共同构成。但是由于混合系统的复杂性，一般难以用单独的数学模型进行描述或表达，因此混合系统一般都是由系统各部分输入与输出间的数学方程所共同描述的。

同样，由于混合系统的复杂性，不存在对应于的连续系统和离散系统中的传递函数模型、零极点模型、状态空间模型等表达方式。一般来说，对于混合系统的分析，只能直接对由系统各部分输入与输出间的数学方程所共同描述的模型进行直接建模仿真分析。

例7：考虑如下的一个混合系统：设系统的输入为一离散变量，系统由离散系统与连续系统串联构成，其中离散系统输出经过一个零阶保持器后作为连续系统的输入。其中离散系统的输入输出方程为 $u(n) = 0.5 \cdot n$ 且系统采样时间为Ts=1 s(即1Hz的采样率)。连续系统的输入输出方程为：

$y(t) = \sqrt{x(t)} + sin(x(t))$

由于此混合系统中离散系统的输出经过一零阶保持器后作为连续系统的输入，因此u(t)与u(n)的数学关系为:

$x(t) = u(n) + 1\quad n T_s \leq t \leq (n+1)T_s$

故此混合系统的输入与输出之间的关系可以由下面的方程来描述：

$\left\{\begin{matrix} \begin{align} u(n) &= 0.5 n \quad n = 1,2,\cdots \\ x(n) &= u(n) + 1 \\ y(t) &= \sqrt{x(n)} + sin(x(n)) \quad n T_s \leq t \leq (n+1)T_s \end{align} \end{matrix}\right.$

5.1 Matlab仿真

close all; clear; clc;

t=1:0.1:99.9; %表示在时间[1，99.9]范围内分析系统。时间间隔0.1 s
n=1:100;      %表示系统输入时刻为1~100 s
un=0.5*n;     %表示系统输入u(n)
yn=un+1;      %表示系统中离散部分的输出，即连续部分的输入

for j=1:length(t)
    n    = floor(t(j)); % 计算对应的离散时间点
    un   = 0.5 * n;
    xn   = un + 1;       % 离散系统的输出。连续系统部分的输入端的零阶保持器的输入
    y(j) = sqrt(xn) + sin(xn);
end

plot(t,y);grid; %绘制系统输出曲线图系统输出曲线

仿真结果如下图所示：

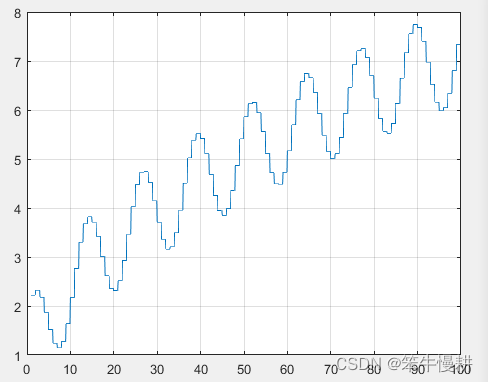
虽说，本系统的后半部分是连续系统，但是计算机仿真究竟只能以离散的方式进行仿真。只不过，如本例中所示，对连续系统仿真时所采用的采样率要足够高即可。

5.2 Simulink建模仿真

以下也给出一个用simulink对以上混合系统进行建模仿真的示例。Simulink模型如下图所示：

最左端的是一个“Free-run counter”，采样周期设置为1，对应于1Hz的采样周期，用以模拟输入端的离散系统。坐起第三个模块是一个Zero-Order Hold模块，最右端是TimeScope模块。“Matlab Function”中实现" y = sin(x)"的功能。对这个系统仿真得到输出波形如下（与上面结果大抵相近，但是似乎初始相位不太相同。作为第一个例子，就不追究这些细节了。后面再来讨论Simulink建模仿真的各方面的问题）：

参考文献

【1】王正林，王胜开，陈国顺，王祺编著，Matlab/Simulink与控制系统仿真

【2】姚俊，马松辉编著，Simulink建模与仿真

笨牛慢耕

关注

4
点赞
踩
45

收藏

觉得还不错? 一键收藏
打赏
0
评论
Matlab/Simulink：动态系统模型的表示及仿真分析基础

本文对Matlab/Simulink建模中常见的动态系统及其表示进行概要性的介绍。按照动态系统是否有记忆可以分为无记忆系统和有记忆系统。按照动态系统在时间域是连续的还是离散的可以分为连续时间系统（简称连续系统）和离散时间系统（简称离散系统）。如果其中既包含连续动态子系统也包含离散动态子系统的话，则可以称为混合时间系统（简称混合系统）。按照系统是否满足线性性可以分为线性系统和非线性系统。按照系统的行为是随时间变化的还是不随时间变化的可以分为时变系
复制链接

扫一扫