（今天继续努力学习！使劲学!）
目录
这两个定理是概率论中非常重要的定理，在理论研究和应用中起着非常重要的作用。极限的引入可以让我们衍生到大量数据当中，以便我们在海量数据中分析数据的特征。
一、大数定律
1. 弱大数定理（辛钦大数定律）
若一组随机变量服从统一分布，且有数学期望μ，作前n个变量的算术平均，则对一任意小的数，大于零，满足算术平均依概率收敛与μ
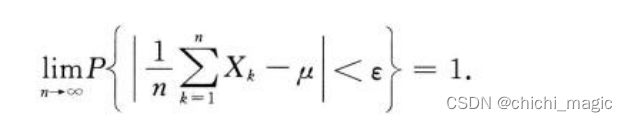
这是一个随机事件，弱大数定理告诉我我们，对于独立同分布、具有数学期望的一组随机变量，当n很大时，它们的算术平均很可能接近于该组随机变量的数学期望。
2. 辛钦大数定律的推论-->伯努利大数定律
依据小概率事件原理，上述事件发生的概率很小，实际推断可知，当试验次数很大时，可以使用事件的频率来代替事件的概率。
论证了频率的稳定性，频率的稳定性是概率稳定性的客观基础。
二、中心极限定理
中心极限定理的客观背景是，在实际生活中，会有多种随机变量，是由大量的相互独立的随机因素的综合影响所形成的的，而其中每一个个别因素在总的影响中起到的作用又非常小，这种随机变量近似地服从正态分布。
1. 独立同分布的中心极限定理
通常，我们有时候很难求出n个变量之和的分布函数，这时候，就可以利用正态分布给出其近似地分布。利用正态分布对n个变量之和作分析或作计算是非常便利的。
这是大样本统计推断的基础。
2. 李雅普诺夫定理
当每个随机变量的数学期望和方差都不相同的时候，使用此定理进行计算。
只要满足定理的条件，那么它们的和当n很大时，就近似服从正态分布，这也是正态随机变量在概率论中占有重要地位的原因。
在很多实际应用中，很多问题都可以表示成很多个独立的随机变量之和。
3. 蒂莫夫-拉普拉斯定力
这个定理表明，正态分布是二项分布的极限分布，当n充分大时，可以利用正态分布来计算
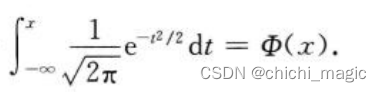
654
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
