反向放大器传递函数推导——史上最全

基本反向电路带输出直流偏置控制功能电路图如下所示，这里尝试用各种不同的思路来推导其传递函数，通过结果我们发现最终将得到一样的传递函数，不同思路可以有助于对运算放大器的工作原理更好理解。

A、利用虚短虚断原理推导：

1、理想运放假设

在理想运放假设下（输入端电流为 0、运放两输入端电压相等），可得：

其中 Vn表示运放反相端的电压。

2、节点方程（KCL）
对反相端节点应用 KCL（节点电流和为零），可得：

3、代入 Vn=Vcmi

将 Vn=Vcmi代入上式：

4、解出 Vout

​整理可得：

若展开该式，则可写成：

以上即该电路的传递函数，若 Zi与 Zf为纯电阻，则它是带有共模偏置项的反相放大器。若 Zi与 Zf为一般阻抗，则只需将上述式子中相应的电阻值替换为阻抗即可。

B、利用叠加原理推导：

下面给出一种常用的“叠加”思路来推导同样的结果。将电路的两个输入视为 Vin​ 和 Vcmi​，分别考虑它们对输出的贡献，再将结果相加即可。

1. 只考虑Vin​ 对输出的影响，令 Vcmi=0V

当Vcmi​=0 时，同相端电压为 0。对理想运放而言，反相端电压与同相端电压相等，故反相端电压也为 0（“虚地”概念）。这样电路就变成了一个标准的反相放大器：反相端电压（节点电位） V−​=0，输入电流经过电阻Zi​，然后流过反馈电阻Zf​ 回到输出端，因此，输出与输入间的关系为

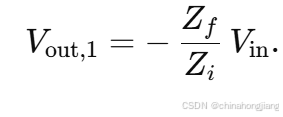
2、只考虑Vcmi​ 对输出的影响，令 Vin=0V

当 Vin​=0 时，输入端接地。而同相端电压为Vcmi​，理想运放令反相端电压也等于 Vcmi​。此时：从“Vin 节点”到反相端的电阻Zi​，其两端电压分别是 0 和Vcmi​。从“输出端”到反相端的反馈电阻Zf​，其两端电压分别是Vout​ 和Vcmi​。

对反相端做 KCL，令流入反相端的电流为正，则

整理可得；

进而得到

3、叠加结果

由于运放是线性器件，最终的输出就是来自Vin​ 和 Vcmi​ 两个独立“激励”贡献的叠加和，即

这与之前直接使用虚短虚断方法一致，只是用“叠加”的思路更直观地看到了输入信号与共模电压各自对输出的贡献。

C、利用极限原理推导：

下面再提供一种常见的“有限增益模型”推导思路：先假设运放有一个非常大的但有限的开环增益 AA，写出运放输出与输入差值之间的关系式，然后令 A→∞A \to \infty 得到极限形式。这个方法在分析某些精密电路时很有用。

1、写出运放的开环模型方程
对于理想运放通常假设“输入差分电压极小”，但若我们引入一个有限增益 A，则

在此电路中，

2、将 V−用 Vout表示
由上式可得

3、对反相端节点 V−写 KCL

反相端节点通过 Zi与 Vin相连，通过 Zf与输出 Vout相连，并假设理想运放输入电流为 0。则

将上一步得到的式子代入，得到

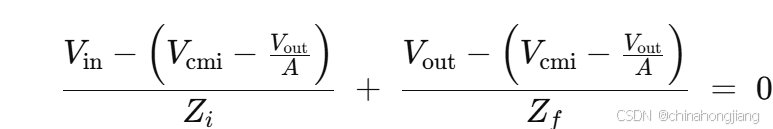
展开并整理，可写成

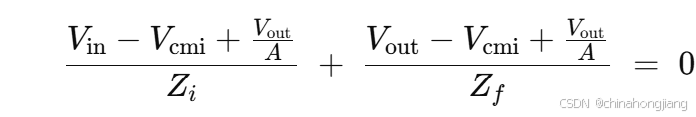
4、令 A→∞并求解 Vout

当 A→∞时，Vout/A项变得可忽略，因此上式简化为

这时再解得

这便是该电路的传递函数。由此可见，若运放增益 A足够大，则反相端电压与同相端电压“几乎相等”，最终得到与前两种思路相同的结果。这样就完成了利用“有限增益模型并令 A→∞求极限的第三种推导方式。

D、参考点平移原理推导：

1、定义新电压变量
假设将同相输入端电压Vcmi​ 当作新的参考零电位。为此，引入新变量v′=v−Vcmi​,

表示对原参考地(系统地)“下移”了Vcmi​。

新的“输入电压”记为Vin′​=Vin​−Vcmi​。

新的“输出电压”记为 Vout′=Vout−Vcmi​。

此时，放大器的非反相端在新参考系下电压为 0（因为它原来是 Vcmi）。

2、在新参考系下，电路变成标准的反相放大器
在这个新参考系里，非反相端是 0V，反相端在理想运放模型下也将贴近 0V（“虚地”）。因此电路就是一个“输入电压为 Vin′​，反相端虚地，负反馈电阻Zf​，输入电阻 Zi​ 的标准反相放大器”。对这样一个“标准反相放大器”而言，新参考系下的输出 Vout′和Vin′​ 的关系是

3、将结果平移回原参考系

由于我们当初“下移”了 Vcmi​，现在要回到最初的电路坐标系，则

展开整理得

这正是我们熟悉的结果。该方法的思路可以概括为：“把同相端视作零电位，就把电路看成一个普通的反相放大器；然后再把输出电平整体上抬回到原先的共模电压处。”这样可以非常快捷地得到该电路的传递函数。