SVD奇异值分解详解

1、定义

假设C是MxN矩阵，U是MxN的矩阵，其中U的列为CC^T的正交特征向量，V为NxN矩阵，其中V的列为C^TC的正交特征向量，再假设r为C矩阵的秩，则存在奇异值分解：

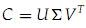
然后把∑的r个对角元素的前k个保留（最大的k个保留）, 后面最小的r-k个奇异值置0, 得到∑k；最后计算一个近似的分解矩阵

则Ck在最小二乘意义下是C的最佳逼近，∑k是∑的低阶近似。

2、SVD相关数学概念

1）矩阵的秩，是矩阵中线性无关的行或列的个数

2）对角矩阵，除对角线外所有元素都为0的方阵

3）单位矩阵，如果对角矩阵所有对角线上元素都为1则称单位矩阵

4）特征值，对于一个MxN的矩阵C和向量x，如果存在λ使得Cx=λx，则称λ为矩阵C的特征值，x为矩阵的特征向量

3、SVD的低阶近似原理

考虑如下矩阵S

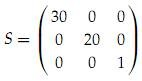
该矩阵的特征值λ1 = 30,λ2 = 20,λ3 = 1。对应的特征向量

‍假设V^T=(2,4,6) 计算S x V^T‍

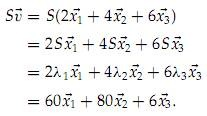
^{由上面计算结果可以看出，矩阵与向量相乘的结果与特征值，特征向量有关。观察三个特征值λ1 = 30,λ2 = 20,λ3 = 1，λ3值最小，对计算结果的影响也最小，如果忽略λ3，那么运算结果就相当于从(60,80,6)转变为(60,80,0)，这两个向量十分相近。这也表示了数值小的特征值对矩阵-向量相乘的结果贡献小，影响小。}

4、SVD的实例

原始文档矩阵C1

低阶近似后的矩阵C2

转载于:https://my.oschina.net/u/2318847/blog/422542