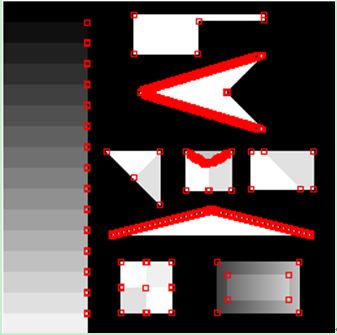
下图中,是用3*3的窗口,对图像进行morave角点检测。虽然moravec算法能把所有角点都检测出来,但是把边缘上面的很多点也作为角点了,对于这种情况,我们应该是可以理解的。moravec算法对角点定义是:窗口在各个方向的移动,窗口内的灰度值都会产生较大的变化。而其实这里的“各个方向“,最多也就只有8个方向。所以,如果边缘的方向,是这8个方向以外的方向,那么,就会被认为是角点。
(1)它不具备旋转不变性。
(2)对边缘点的反应比较强烈
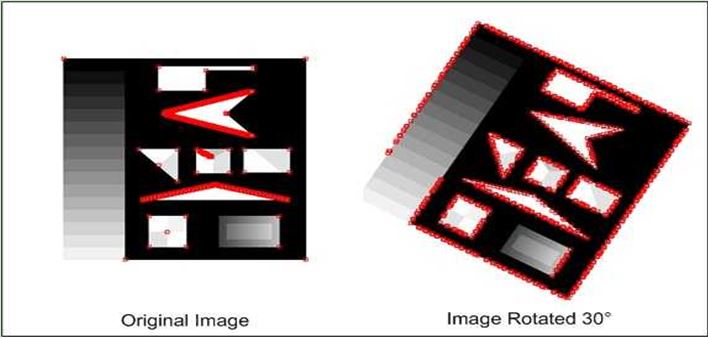
moravec只计算了一些离散的偏移产生的灰度值变化(最多是8个方向),如图下所示,旋转之后,检测到角点不一样了。moravec统计的8个方向(最多是8个方向)是0°,45°,90°,135°,180°,225°,270°,315°。如果图像上的边缘上的某个点,在旋转前刚好是处于45°方向,此时检测到不是角点(因为窗口在45°方向平移的时候,窗口内部像素值变化肯定很小),当图像旋转10°,此时该点处在55°,那么现在就很有可能变成了一个角点(因为窗口只有在55°方向平移的时候,窗口内部的灰度值变化才会取到最小值,而55°不在moravec算法的统计之内)
在moravec中,使用的窗口是正方形的,并且窗口值是二元的,在窗口内,窗口值是1,在窗口外,窗口值是0,公式:
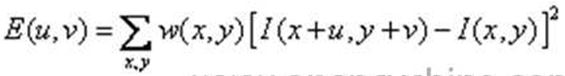
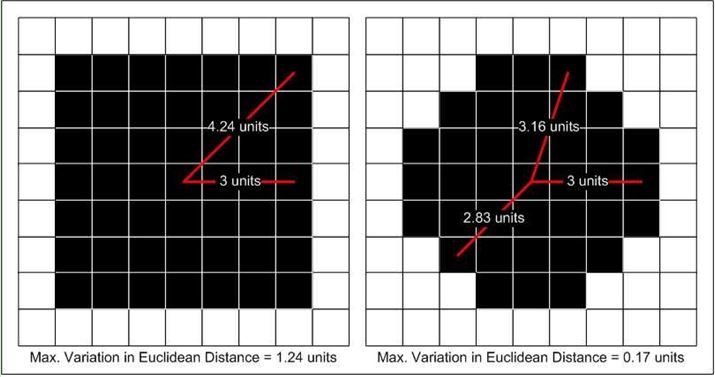
为了达到精确估计局部灰度值的变化程度,圆形的窗口才是理想的。圆形的窗口,使得中心点到窗口的每一个边缘点的欧式距离基本是相等的。如图,左图是7*7窗口,右图是半径为7的圆形窗口,可以看出,对于圆形窗口,从中心点到各个边缘点之间的欧式距离更接近。这样更有利于评估局部灰度值的变化程度。为什么呢?“评估局部灰度值的变化程度“,注意这句话里的一个关键词” 局部“,那么什么是局部?如果我们使用7*7的正方形窗口,那么这个正方形窗口就是局部,我们的评估局部灰度值的变化程度的时候,这49个元素都会参与运算;当我们使用半径为7的圆形窗口的时候,那么这个半径为7的圆形窗口就是局部,在这个圆形窗口内的灰度值都会参与运算。
通常,我们认为,里中心点更近的点,对该点影响也会大一些。既然离得比较近的点对中心点的影响比较大,那么我们在评估局部灰度值的变化程度的时候,应该赋予离中心更近的点更大的权重才是合理的,而不是moravec使用的窗口值,只要在窗口内部,不管远近,权重都是1.

moravec的局限性分析
(1)它不具备旋转不变性。
(2)对边缘点的反应比较强烈
moravec只计算了一些离散的偏移产生的灰度值变化(最多是8个方向),如图下所示,旋转之后,检测到角点不一样了。moravec统计的8个方向(最多是8个方向)是0°,45°,90°,135°,180°,225°,270°,315°。如果图像上的边缘上的某个点,在旋转前刚好是处于45°方向,此时检测到不是角点(因为窗口在45°方向平移的时候,窗口内部像素值变化肯定很小),当图像旋转10°,此时该点处在55°,那么现在就很有可能变成了一个角点(因为窗口只有在55°方向平移的时候,窗口内部的灰度值变化才会取到最小值,而55°不在moravec算法的统计之内)

在moravec中,使用的窗口是正方形的,并且窗口值是二元的,在窗口内,窗口值是1,在窗口外,窗口值是0,公式:
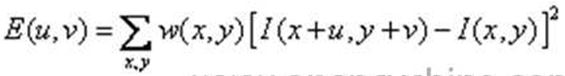
为了达到精确估计局部灰度值的变化程度,圆形的窗口才是理想的。圆形的窗口,使得中心点到窗口的每一个边缘点的欧式距离基本是相等的。如图,左图是7*7窗口,右图是半径为7的圆形窗口,可以看出,对于圆形窗口,从中心点到各个边缘点之间的欧式距离更接近。这样更有利于评估局部灰度值的变化程度。为什么呢?“评估局部灰度值的变化程度“,注意这句话里的一个关键词” 局部“,那么什么是局部?如果我们使用7*7的正方形窗口,那么这个正方形窗口就是局部,我们的评估局部灰度值的变化程度的时候,这49个元素都会参与运算;当我们使用半径为7的圆形窗口的时候,那么这个半径为7的圆形窗口就是局部,在这个圆形窗口内的灰度值都会参与运算。

通常,我们认为,里中心点更近的点,对该点影响也会大一些。既然离得比较近的点对中心点的影响比较大,那么我们在评估局部灰度值的变化程度的时候,应该赋予离中心更近的点更大的权重才是合理的,而不是moravec使用的窗口值,只要在窗口内部,不管远近,权重都是1.
通过上面的分析,既要使用圆形的窗口,又要赋予离中心更近的点更大的权重,那么高斯窗口就是比较好的一个选择了。5*5的高斯窗口如图所示:虽然看起来的也是方形的,但是它在四个角落上的权重是非常小的,可以近似的认为是0,那么就可以认为是一个圆形的窗口,并且,权重是离中心点越近变得越大。























 7874
7874

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








