PMSM是一个强耦合、复杂的非线性系统,要实现更好的控制建立合适的数学模型就显得尤为重要,主要包括同步旋转坐标系、静止坐标系下的数学模型,以及动态模型。
三相PMSM的坐标变换
1.1 Clark变换(3s->2s)
将自然坐标系ABC变换到两相静止坐标系的变换称为Clark变换,变换以产生相等的磁动势以及相等的电压或电流幅值(或相等的电功率)为准则。由产生相等的电压或电流幅值和相等的电功率可分为等幅值变换以及等功率变换。
1.1.1 等幅值变换
等幅值变换与等功率变换本质上是对转换得到的两相静止坐标系进行缩放处理。先 写出变换前后的电压(将三相电压表示为表示):
合成得到的电压矢量为
变换到两相静止坐标系后:
示意图如下图所示:

写出最终合成电压的幅值为 ,为保证变换后的幅值与三相静止坐标系的幅值
相等,则需要再变换时额外乘
才满足,得到最终的变换式为
最后一行只有当三相正弦量不对称时才会有值(零序电流),一般对称的情况下不考虑,并且零序电流不产生合成磁场。
和
轴物理量幅值与原三相电路幅值保持一致,对应转矩公式省去开头的3/2。
1.1.2 等功率变换
先分别计算变换前后的有功功率(与等幅值变换时相同,投影到两相轴时幅值将变为原有的3/2倍):
将变换后的两相坐标值均乘一个系数k,得到此时的有功功率为:
令 得:
得到最终的变换公式为
最终,两相坐标系物理量的幅值将变为原三相电路幅值的倍,对应转矩公式要保留开头的3/2。
1.1.3 补充
上述情况属于d轴起始位置与A轴重合时(对应Matlab中的"Aligned with phase A axis")。当q轴的起始位置与A轴重合时(对应Matlab中的"90 degrees behind phase A axis"),此时的Clark变换有所不同,示意图如下图所示:

1.等幅值Clark变换(qa重合)
2.等功率Clark变换(qa重合)
1.2 Park变换(2s->2r)
将静止坐标系(图中为
)变换到同步旋转坐标系
的坐标变换称为Park变换。由于
坐标系是以转子磁场同步旋转的,所以变换矩阵与两坐标系的夹角
有关。其示意图如下图所示:

Park变换只需要将原有坐标系投影到同步旋转坐标系即可,变换矩阵为:
要从三相静止坐标系变换至同步旋转坐标系,只需要分别进行上述两次变换即可。
1.2.1 补充
当使用qa重合的Clark变换时,注意进行Clark+Park变换时,需要对进行转置处理(因为qa重合的Clark变换,
分量的位置互换了)
1.2.2 指数形式的Park变换
两相静止坐标系中相量的相位为,而两相旋转坐标系中相量的相位为
,两个坐标系间的相位差为
,得到各坐标系的坐标为:
1.3 Clark+Park变换(3s->2r)
1.3.1 等幅值da重合
1.3.2 等幅值qa重合
1.3.3 等功率da重合
1.3.4 等功率qa重合
1.4 仿真建模
1.4.1 等幅值Clark变换


两个matlab函数中分别为


1.4.2 Park变换

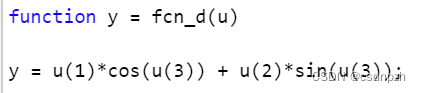
























 3702
3702

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








