【论文学习】半马尔科夫随机跳变系统的随机稳定性与鲁棒镇定（随机稳定性分析）

J o s k i

于 2023-11-15 18:10:00 发布

阅读量1.5k

点赞数 9

文章标签：学习

本文链接：https://blog.csdn.net/csdnqiezi/article/details/134290417

版权

一、论文出处

Ji Huang and Yang Shi，Stochastic stability and robust stabilization of semi-Markov
jump linear systems，INTERNATIONAL JOURNAL OF ROBUST AND NONLINEAR CONTROL
Int. J. Robust Nonlinear Control 2013; 23:2028–2043

DOI: 10.1002/rnc.2862

二、简写说明

1.马尔可夫跳变线性系统：Markov jump linear systems (MJLSs)。

2.半马尔可夫跳跃线性系统：semi-Markov jump linear system(S-MJLS)。

三、随机稳定性证明

首先给出一个证明S-MJLS的鲁棒随机稳定性的引理：

若 $F^{\boldsymbol{\mathbf{T}}}F\leq I$ ，存在常数矩阵 $H$ 和 $E$ ，和标量 $\varepsilon > 0$ ，使以下不等式成立：接着抛出自己的定理：

若存在一组矩阵 $P(i)> 0$ ， $i\in S$ ,和一组正标量 $\varepsilon_{A,i}> 0$ , $i\in S$ 使下列容许不等式成立：

证明过程如下：选取二次型Lyapunov函数：

$V(x(t),r(t))=x^{\mathbf{T}}(t)P(r(t))x(t)$ .

其中， $P(r(t))$ 为正对称矩阵，无穷小生成元（即无穷小算子，详见随机过程理论） $\tilde{A}$ 被视为李雅普诺夫函数沿半马尔科夫过程在时间 $t$ 轨迹的导数（此处原文给出了出处，详见引文）。首先导出无穷小生成元，根据其定义，有：

此处的 $\bigtriangleup$ 是小正数，接着，在 $r(t)=1$ 的条件下应用全概率公式及条件期望公式，将以上公式转化为：

上式是按 $t+\Delta$ 时刻状态与 $t$ 的同异划分成前后两部分，使用全概率公式展开。接着文章使用条件概率公式进一步展开：这一步很好理解，不再赘述。

对于MJLSs的无记忆特性（理解为指数分布），有以下变换：

$\mathrm{Pr}\left \{ r(t+\Delta ) =j,r(t)=i\right \}=\mathrm{Pr}\left \{ r(\Delta ) =j,r(0)=i\right \}$ .

即：系统变换仅与时间增量有关，与所处时刻无关。

但对于S-MJLSs，该式不成立，因为转移率是时变的，是取决于 $h$ 的函数。这里定义系统从状态 $i$ 跳跃到状态 $j$ 的概率为 $q_{ij}$ ，当系统保持在模式 $i$ 时，sojourn-time $h$ 的累积分布函数（CDF）为 $G_{i}$ ，从最后一次跳跃开始，停留在模式 $i$ 的时间为 $h$ ，重新改写（6）式，得到如下结果：

这里将上边的条件概率展开成两式相乘，即状态跳变的概率乘以两不同时刻CDF的差值（再停留一个 $\Delta$ 时间的概率），CDF是概率直观的表达。在 $r(t)$ 时刻处于状态 $i$ 的概率可以理解成停留时间大于等于 $h$ 的概率，也就是 $1-G_{i}(h)$ .

利用一阶近似（泰勒一阶展开），将 $x(t+\Delta )$ 写为

则可将无穷小生成元写为

其中， $Q(i,h,t)$ 由下式表示：

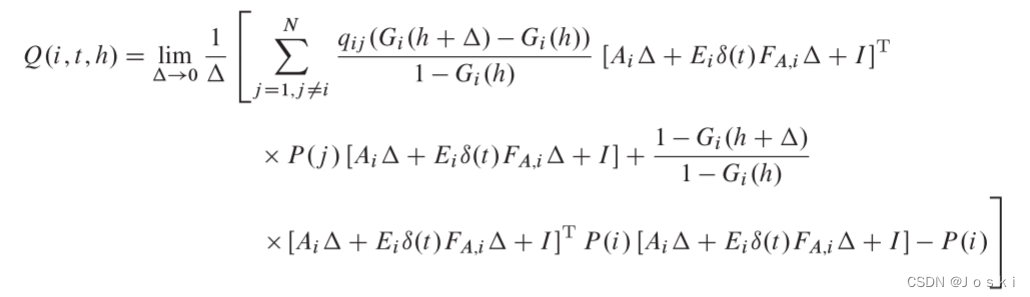
移项，改写为这里主要是为了凑出 $\lim_{\Delta \to 0}\frac{G_{i}(h+\Delta )-G_{i}(h)}{(1-G_{i}(h))\Delta }$ 和 $\lim_{\Delta \to 0}\frac{G_{i}(h+\Delta )-G_{i}(h)}{1-G_{i}(h) }$ 这两项。

根据分布函数的性质，有：先看后面一项，分子是逗留时间为 $h+\Delta$ 与 $h$ 的概率之差，由于 $\Delta$ 太小，分子是无穷小，后一项必然为0。前一项相当于分布函数求导后再与分母的有限量作比值，将该项定义为 $\mathit{\lambda }_{i}(h)$ 。

据此将 $Q(i,h,t)$ 化简为：

在这里引出 $\mathit{\lambda }_{ij}(h)$ 和 $\mathit{\lambda }_{ii}(h)$ 的数学定义：

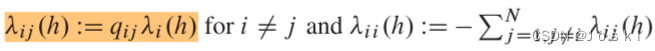
这里就是转移概率矩阵中各元素的定义了。接着化简：将划红线部分用引理1进行放缩，有将 $Q(i,h,t)$ 以放缩项换元，重新定义显然，有 $Q(i,h,t)\leq \tilde{Q}(i,h)$ 。

使用舒尔补[此处为矩阵理论相关知识]将所需证明的 $\tilde{Q}(i,h)< 0$ 转化为以下矩阵形式：

其中， $J_{i}(h)$ 由以下表示：

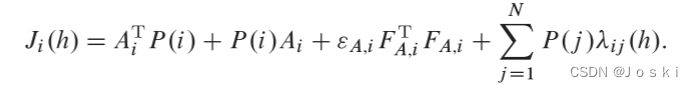因此，为了证明以下不等式链成立：

还需证明

存在。将 $\tilde{Q}(i,h)$ 拆成以下两项：

其中，显然，这两项的 $\lambda _{\mathrm{max}}$ 均存在，因为 $\lambda _{ij}(h)$ 正定且有上界： $\bar{\lambda _{ij}}$ .因此，以下两个不等式成立：

表示都为半负定矩阵。所以以下不等式成立：

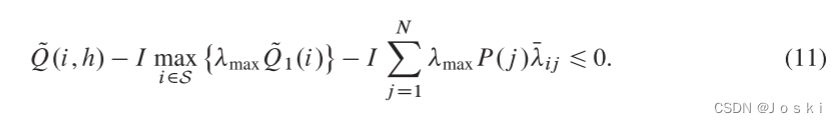这就证明了不等式链的正确性。最后，使用广义Dynkin公式，有

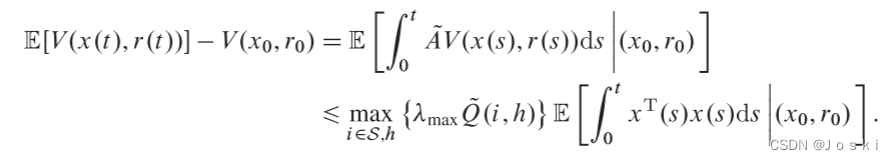移项，即可得到

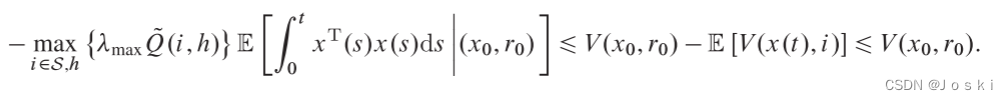由（4）中定义的条件，

即得下式对任意 $t> 0$ 均成立：

当有界，则以上不等式左边被右边的正常数所限定。根据最初对S-MJLSs系统随机稳定性的定义，系统是随机稳定的，完成了证明。