网络流学习笔记（3）：最小费用流与其反向弧详解+算法模板

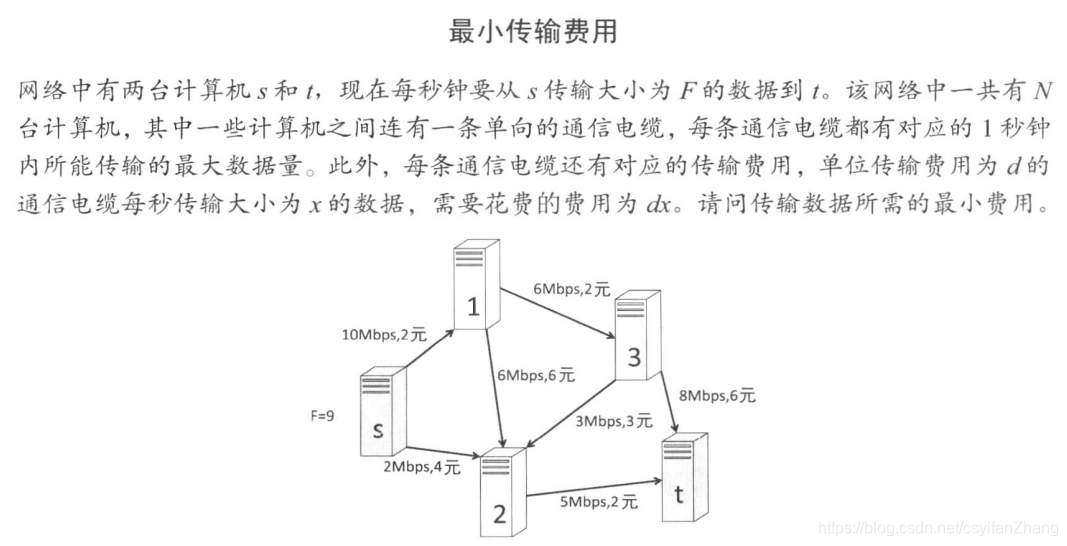
根据网络流相关的知识，可以以计算机为顶点，通信电缆为边，从而得到一个有向图，每条边$e$都有容量$c(e)$和费用$d(e)$。题目可以理解为，保证从$s$到$t$有流量为$F$的流的前提下，使得费用${\sum }_e(f(e)\ast d(e))$最小。

这就是在最大流问题的网络中，给边新加上了费用，而求的不再是流量的最大值，而是流量为F 时费用的最小值。这类问题叫做最小费用流问题。

接下来，让我们来考虑一下这类问题的解法。求解最大流时，我们在残余网络上不断贪心地增广而得到了最大流。现在边上多了费用，如果我们在残余网络上总是沿着最短路增广又如何呢？此时，残余网络中的反向边的费用应该是原边费用的相反数，以保证过程是可逆而正确的。为什么？如果让我们来设置反向边的费用又该如何设计？首先我们原边与反向边的花费数值上一定要保持一致，毕竟本质上是一条路，正反走应该都差不多。那么直接让二者相等吗？要知道，反向弧设计的初衷，是给我们的算法提供一个后悔的机会反向弧理解，而最小费用流的后悔要如何理解？我们先按照花费相等建立一个残余网络：

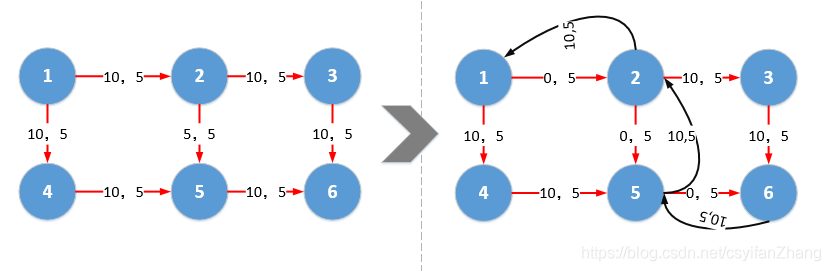
假设我们第一次走了1-2-5-6，然后建立了该残余网络，此时到2,5,6的花费分别为0+5*10,5*10+5*10,5*10+5*10+5*10，如果我们要用这个反悔的机会，那么在把2->5的流量退回2时，就有如下更新cost[2]=cost[5]+10*5???显然和我们的意图不太一样，我们需要令2的花费保持原状，如果此时的花费是-5呢？那么我们有cost[2]=cost[5]-5*10，流量成功退回而且花费也保持在原状。

因为有了负权边，所以就不能用 Dijkstra算法求最短路了，而需要用Bellman-Ford算法。

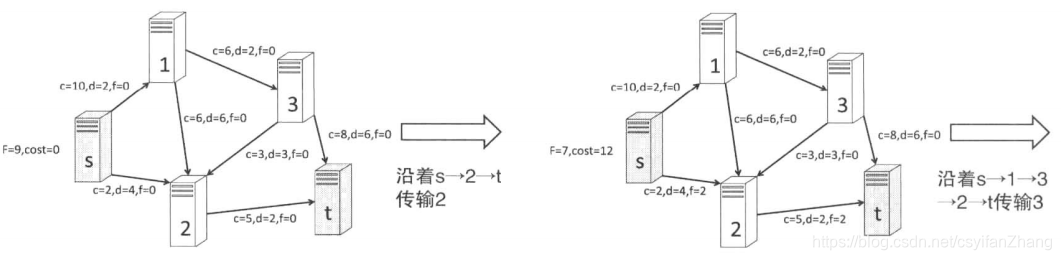
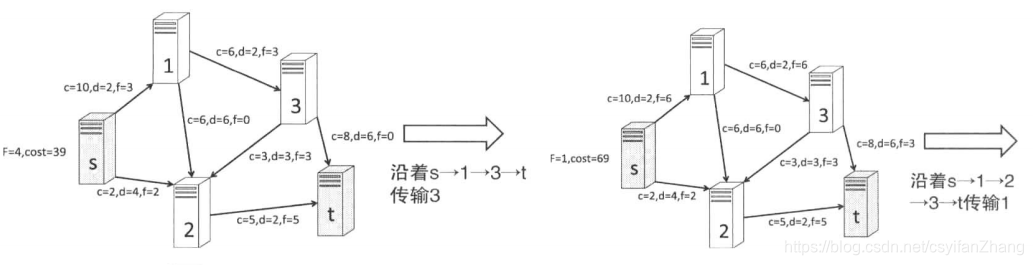
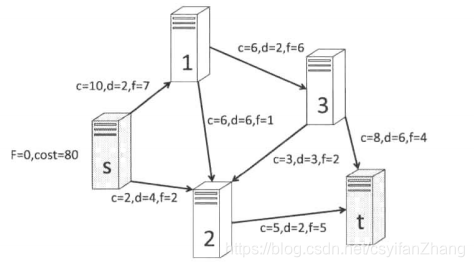
tips：以下是最小费用最大流的代码，固定流的话其实差别不大。我们只需要不断的更新最大流，直到他超过了预期的流量。

#include<bits/stdc++.h>
using namespace std;
const int maxn=123456789;
struct node{
    int to;//这条边的终点 
    int cap;//这条边的流量（是指当前还能流的最大流量，而不是不变量） 
    int coc;//coc存反向边。由于我使用了vector，所以coc记录的是data[x][i]中的i。具体怎么计算反向边下面说。 
    int cost;//cost存一条边的费用 
};//使用一个结构体存储所有的边以及反向边，所有边都是无向边。 
vector<node>data[50005];//data用来存图 
int dx[50005],pre1[50005],pre2[50005],incf[50005],n,m,s,t,ans,maxf;
bool inq[50005];
// dx，inq的意义和spfa中的dist，inq（或vis）相同，pre1，pre2，incf的用处下面会说。
// n,m,s,t如题目所示，ans是最小费用，maxf是最大流。 
void add(int u,int v,int w,int f){//加一条边的函数，由u到v连一条流为w，花费为f的边 
    data[u].push_back((node){v,w,data[v].size(),f});
    data[v].push_back((node){u,0,data[u].size()-1,-f});//反向边的流要置为0。因为如果你设成正的，这条路就有可能由终点向起点流，在另一条路上达到最大流，更小费用。这显然不合法。 
    //反向边的实现，是考虑到这两条互为反向边的边是同时加入的，直接调用当时data[v].size()就是反向边的编号。
    //按说用size()计算编号是应该-1的（因为编号由0开始，而size()由1开始），但是第一个计算不用，原因是
    //当时v还没有插入这个边，天然有一个被减一的size() 
}
bool spfa(){
    fill(dx+1,dx+n+1,maxn);//初始化，一定别忘了。 
    queue<int>q;
    memset(inq,0,sizeof(inq));
    q.push(s);
    dx[s]=0;
    inq[s]=1;//以上这些变量，玩转spfa的你一定看起来很熟悉QAQ 
    incf[s]=maxn;//那么incf呢？他记录的是一条增广路的最小流量。incf[i]代表当前增广路到i为止的最小流量，incf[t]为整条路最小流量。 
    //如何理解呢，我们考虑短板效应，最大容量取决于最短木板。增广路亦然，它的最大流量取决于增广路上流量最小的边。 
    while(!q.empty()){
        int now=q.front();
        inq[now]=0;
        q.pop();//是不是超熟悉的感觉QAQ (只说一下和spfa不一样的代码的意思)
        for(int i=0;i<data[now].size();i++){
            node &tmp=data[now][i];
            if(tmp.cap>0&&tmp.cost+dx[now]<dx[tmp.to]){//有流量才能松弛~ 
                dx[tmp.to]=dx[now]+tmp.cost;//和spfa一样 
                incf[tmp.to]=min(incf[now],tmp.cap);//更新增广路的“短板”。
                pre1[tmp.to]=now;//pre1[i]是这次增广路的i点是由哪个点流过来的。 
                pre2[tmp.to]=i;//pre2[i]是这次增广路的i点是由pre1[i]的编号为多少的边流过来的。 
                if(!inq[tmp.to]){//QAQ spfa，spfa你还活着！ 
                    inq[tmp.to]=1;
                    q.push(tmp.to);
                }
            }
        }
    }
    return dx[t]!=maxn;//如果dx[t]被更过了，意味着一定不是最大流！返回1，找增广路去！ 
}
void update(){//更新答案和图程度的能力。 
    int x=t;//首先把当前点置为终点，我们沿着终点由增广路反向走到起点~ 
    while(x!=s){//x到s的时候停止~ 
        int y=pre1[x];//使用我们先前维护的数组来反向走增广路。 
        int i=pre2[x];
        data[y][i].cap-=incf[t];//所有增广路上的边一律减去可扩最大容量！ 
        data[x][data[y][i].coc].cap+=incf[t];//反向边，一律增加这个容量。
        //如果说为什么要弄反向边，我个人的理解是：增广一条增广路费用最优，然而最大流量未必。
        //如果我们反向建边，可以由终点流向起点，这样其实意味着，当年这条边选择的流减少一点。
        //不过我们未必要理性理解这个事，既然都建了反向边了，那就和正向边反着来呗~
        x=y;//迭代一下 
    }
    maxf+=incf[t];//更新最大流 
    ans+=dx[t]*incf[t];//更新费用 
}
void FT(){
    while(spfa()){//当spfa发现有增广路的时候，就更新一下图，最小费用和最大流。如果没有增广路，答案最优。 
        update();
    }
}
/*
    最小费用流其实并不难，而且非常好用/w\可以解决很多乱七八糟的问题。
    代码难度较低，建图难度较高。如SDOI2017新生舞会。
    个人认为，用这样鬼畜的建模方式，恐怕难以卡掉spfa。
    为什么找增广路用spfa就可以做到最小费用呢？考虑我们每一次的松弛都是以一条路径的方式松弛过来的，尽管
    会发散出去，但松弛到一个指定的终点一定有且只有一条路。如果已经不可松弛，这条路一定是当前单位流量价格
    最小的增广路。我们贪心：反正都是增广路，先扩便宜的肯定好啊QAQ 
*/
int main(){
    cin>>n>>m>>s>>t; 
    for(int i=1;i<=m;i++){
        int u,v,w,f;
        cin>>u>>v>>w>>f;
        add(u,v,w,f);//按照题意建图 
    }
    FT();//最小费用流主体 
    cout<<maxf<<" "<<ans<<endl;
}