Soft-Margin 的含义
所谓的Hard-Margin,就是指所有的资料都要完全分开,即separable,这是SVM产生过拟合的原因之一(还有一个原因就是过于复杂的转换
Φ
\Phi
Φ)。
所以引入Soft-Margin, 即不必让所有的资料都完全分开,让SVM容许一部分的错误分类点的存在,从而在一定程度上减少过拟合,即要在large margin 和错误分类点容忍度(noise tolerance)之间做一个取舍,以一个参数来衡量。
选择什么参数来衡量? 以下由两种方式:
第一种方式:衡量错误分类点的个数
min
b
,
w
1
2
w
T
w
+
C
⋅
∑
n
=
1
N
[
[
y
n
≠
s
i
g
n
(
w
T
z
n
+
b
)
]
]
s
.
t
.
      
y
n
(
w
T
z
n
+
b
)
≥
1
  
f
o
r
  
c
o
r
r
e
c
t
  
n
          
y
n
(
w
T
z
n
+
b
)
≥
−
∞
  
f
o
r
  
i
n
c
o
r
r
e
c
t
  
n
\begin{array}{l} \mathop {\min }\limits_{b,w} \frac{1}{2}{w^T}w + C \cdot \sum\limits_{n = 1}^N {\left[\kern-0.15em\left[ {{y_n} \ne sign({w^T}{z_n} + b)} \right]\kern-0.15em\right]} \\ \\ s.t.\;\;\;{y_n}({w^T}{z_n} + b) \ge 1{\kern 1pt} {\kern 1pt} \;for\;correct\;n\\ \\ \;\;\;\;\;{y_n}({w^T}{z_n} + b) \ge - \infty {\kern 1pt} \;for\;incorrect\;n \end{array}
b,wmin21wTw+C⋅n=1∑N[[yn̸=sign(wTzn+b)]]s.t.yn(wTzn+b)≥1forcorrectnyn(wTzn+b)≥−∞forincorrectn
C的含义:trade-off of large margin & noise tolerance。
对于这种方式有两个不足之处,
- [ [ ] ] \left[\kern-0.15em\left[ {} \right]\kern-0.15em\right] [[]]是非线性函数,无法使用QP来求解。
- 无法区分noise点犯错误程度的大小。
第二种方式:衡量错误分类点的犯错误程度
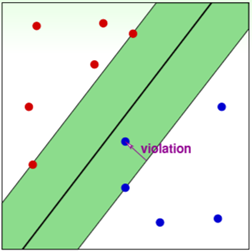
min b , w , ξ 1 2 w T w + C ⋅ ∑ n = 1 N ξ n s . t .        y n ( w T z n + b ) ≥ 1 − ξ n               ξ n ≥ 0            \begin{array}{l} \mathop {\min }\limits_{b,w,\xi } \frac{1}{2}{w^T}w + C \cdot \sum\limits_{n = 1}^N {{\xi _n}} \\ \\ s.t.\;\;\;{y_n}({w^T}{z_n} + b) \ge 1 - {\kern 1pt} {\kern 1pt} {\xi _n}\;\\ \\ \;\;\;\;\;{\xi _n} \ge 0\\ \\ \;\;\;\;\; \end{array} b,w,ξmin21wTw+C⋅n=1∑Nξns.t.yn(wTzn+b)≥1−ξnξn≥0
C的含义:trade-off of large margin & margin violation。
该问题可以用QP来解,即有 d ~ + 1 + N \tilde d + 1 + N d~+1+N个变量,2N个约束。
综上,一般采用第二种方式。
对偶形式的Soft-Margin SVM
构造拉格朗日方程如下,
L
(
w
,
b
,
ξ
,
α
,
β
)
=
1
2
w
T
w
+
C
⋅
∑
n
=
1
N
ξ
n
+
∑
n
=
1
N
β
n
(
−
ξ
n
)
                            
+
∑
n
=
1
N
α
n
(
1
−
ξ
n
−
y
n
(
w
T
z
n
+
b
)
)
\begin{array}{l} L(w,b,\xi ,\alpha ,\beta ) = \frac{1}{2}{w^T}w + C \cdot \sum\limits_{n = 1}^N {{\xi _n}} + \sum\limits_{n = 1}^N {{\beta _n}( - {\xi _n})} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; + \sum\limits_{n = 1}^N {{\alpha _n}(1 - {\xi _n} - {y_n}({w^{\rm{T}}}{z_n} + b))} \end{array}
L(w,b,ξ,α,β)=21wTw+C⋅n=1∑Nξn+n=1∑Nβn(−ξn)+n=1∑Nαn(1−ξn−yn(wTzn+b))
所对应的dual形式描述如下,
max
α
n
≥
0
,
β
n
≥
0
(
min
b
,
w
,
ξ
    
1
2
w
T
w
+
C
⋅
∑
n
=
1
N
ξ
n
+
∑
n
=
1
N
β
n
(
−
ξ
n
)
                            
+
∑
n
=
1
N
α
n
(
1
−
ξ
n
−
y
n
(
w
T
z
n
+
b
)
)
)
\begin{array}{l} \mathop {\max }\limits_{{\alpha _n} \ge 0,{\beta _n} \ge 0} (\mathop {\min }\limits_{b,w,\xi } \;\;\frac{1}{2}{w^T}w + C \cdot \sum\limits_{n = 1}^N {{\xi _n}} + \sum\limits_{n = 1}^N {{\beta _n}( - {\xi _n})} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; + \sum\limits_{n = 1}^N {{\alpha _n}(1 - {\xi _n} - {y_n}({w^{\rm{T}}}{z_n} + b))} ) \end{array}
αn≥0,βn≥0max(b,w,ξmin21wTw+C⋅n=1∑Nξn+n=1∑Nβn(−ξn)+n=1∑Nαn(1−ξn−yn(wTzn+b)))
下面是一系列的求解,
∂ L ∂ ξ n = 0 = C − α n − β n ⇒ β n = C − α n 0 ≤ α n ≤ C ∂ L ∂ b = 0 = ∑ n = 1 N α n y n ∂ L ∂ w i = 0 = w − ∑ n = 1 N α n y n z n ⇒ w = ∑ n = 1 N α n y n z n \begin{array}{l} \frac{{\partial L}}{{\partial {\xi _n}}} = 0 = C - {\alpha _n} - {\beta _n} \Rightarrow \begin{array}{} {{\beta _n} = C - {\alpha _n}}\\ {0 \le {\alpha _n} \le C} \end{array}\\ \frac{{\partial L}}{{\partial b}} = 0 = \sum\limits_{n = 1}^N {{\alpha _n}{y_n}} \\ \frac{{\partial L}}{{\partial {w_i}}} = 0 = w - \sum\limits_{n = 1}^N {{\alpha _n}{y_n}{z_n}} \Rightarrow w = \sum\limits_{n = 1}^N {{\alpha _n}{y_n}{z_n}} \end{array} ∂ξn∂L=0=C−αn−βn⇒βn=C−αn0≤αn≤C∂b∂L=0=n=1∑Nαnyn∂wi∂L=0=w−n=1∑Nαnynzn⇒w=n=1∑Nαnynzn
标准的Soft-Margin SVM Dual形式为,
s t a n d a r d s o f t − m a r g i n S V M d u a l min α 1 2 ∑ n = 1 N ∑ m = 1 N α n α m y n y m z n T z m − ∑ n = 1 N α n s . t . ∑ n = 1 N y n α n = 0 ; 0 ≤ α n ≤ C , f o r n = 1 , 2 , ⋯   , N i m p l i c i t y      w = ∑ n = 1 N α n y n z n                      β n = C − α n \begin{array}{l} {\rm{standard soft - margin SVM dual}}\\ \mathop {\min }\limits_\alpha {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{2}\sum\limits_{n = 1}^N {\sum\limits_{m = 1}^N {{\alpha _n}} } {\alpha _m}{y_n}{y_m}z_n^T{z_m} - \sum\limits_{n = 1}^N {{\alpha _n}} \\ s.t.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{n = 1}^N {{y_n}} {\alpha _n} = 0;\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \le {\alpha _n} \le C,{\kern 1pt} for{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} n = 1,2, \cdots ,N\\ {\rm{implicity}}\;\;{\rm{w = }}\sum\limits_{n = 1}^N {{\alpha _n}{y_n}{z_n}} \\ \;\;\;\;\;\;\;\;\;\;{\beta _n} = C - {\alpha _n} \end{array} standardsoft−marginSVMdualαmin21n=1∑Nm=1∑NαnαmynymznTzm−n=1∑Nαns.t.n=1∑Nynαn=0;0≤αn≤C,forn=1,2,⋯,Nimplicityw=n=1∑Nαnynznβn=C−αn
上述形式类似于hard-margin SVM dual,其实与hard-margin相比,只是在 α n {\alpha _n} αn处多了一个上界C而已。
显而易见,上述形式的SVM可用QP来求解,其共有N个变量,2N+1条约束。
类似的,Kernel也可以用在soft-margin SVM里,此时,参数为,
α
←
Q
P
(
Q
D
,
p
,
A
,
c
)
w
←
∑
n
=
1
N
α
n
y
n
z
n
\begin{array}{l} \alpha \leftarrow QP({Q_D},p,A,c)\\ w \leftarrow \sum\limits_{n = 1}^N {{\alpha _n}{y_n}{z_n}} \end{array}
α←QP(QD,p,A,c)w←n=1∑Nαnynzn
类似于hard-margin,通过SV求解b,有,
S
V
(
α
s
>
0
)
⇒
b
=
y
s
−
y
s
ξ
s
−
w
T
z
s
\begin{array}{l} SV({\alpha _s} > 0)\\ \Rightarrow b = {y_s} - {y_s}{\xi _s} - {w^T}{z_s} \end{array}
SV(αs>0)⇒b=ys−ysξs−wTzs
上式在计算b的时候,有一项
y
s
ξ
s
{y_s}{\xi _s}
ysξs,其中的
ξ
s
{\xi _s}
ξs是在求出b之后才能得到的,所以要想办法去掉该项,这里引入free的概念,即,
f
r
e
e
(
α
s
<
C
)
⇒
ξ
s
=
0
\begin{array}{l} free({\alpha _s} < C)\\ \Rightarrow {\xi _s} = 0 \end{array}
free(αs<C)⇒ξs=0
所以,在soft-margin SVM里,b是通过
f
r
e
e
  
S
V
(
x
s
,
y
s
)
free\;SV({x_s},{y_s})
freeSV(xs,ys)来求解的,即,
b
=
y
s
−
∑
S
V
α
n
y
n
K
(
x
n
,
x
s
)
b = {y_s} - \sum\limits_{SV} {{\alpha _n}{y_n}K({x_n},{x_s})}
b=ys−SV∑αnynK(xn,xs)
当然,也可能存在没有free SV的情况,那这时b只能通过一系列的不等式来限制,此时b的值有很多个,只要满足KKT条件就行。但绝大多数的情形,都是存在free SV的。
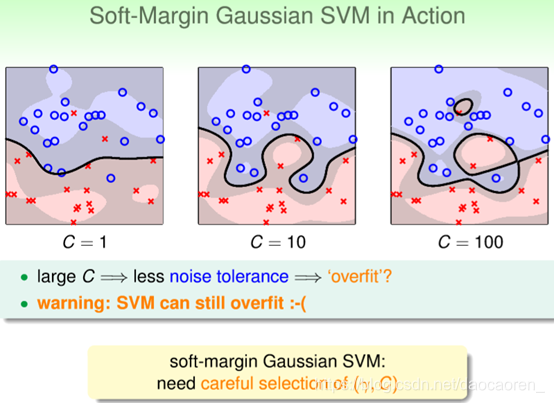
参数选择例子,
α
n
{\alpha _n}
αn的含义,
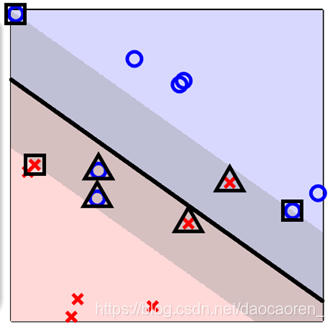
对于SV(
α
n
>
0
{\alpha _{\rm{n}}} > 0
αn>0),分为两种,
1.Free SV(正方形表示):
0
<
α
n
<
C
,
ξ
n
=
0
0 < {\alpha _n} < C,{\xi _n} = 0
0<αn<C,ξn=0,在边界上,用于确定b;
2.Bounded SV(三角形表示):
α
n
=
C
,
ξ
n
=
v
i
o
l
a
t
i
o
n
  
a
m
o
u
n
t
{\alpha _n} = C,{\xi _n} = violation\;amount
αn=C,ξn=violationamount ,违反边界或在边界上
对于非SV(
α
n
=
0
{\alpha _n} = 0
αn=0),有,
ξ
n
=
0
{\xi _n} = 0
ξn=0 ,远离边界或者在边界上
综上, α n {\alpha _n} αn可用在资料分析方面上。





















 396
396











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








