Definitions
Ruled Surface:
– A surface S is ruled (also called a scroll) if through every point of S there is a straight line that lies on S.
– A ruled surface is a surface that can be swept out by moving a line in space.
The “moving line” view means that a ruled surface has a parametric representation of the form S(t,u)=p(t)+ur(t) S ( t , u ) = p ( t ) + u r ( t ) where S(t,u) S ( t , u ) is the generic point on the surface, p(t) p ( t ) is a point that traces a regular curve (i.e., p′(t) p ′ ( t ) never vanishes) lying on the surface, and r(t) r ( t ) is a unit-length vector that traces a curve on the unit sphere. p(t) p ( t ) is called the directrix (also called the base curve) and r(t) r ( t ) is the director curve. For each fixed t t we get a line lying in the surface, and these are the rulings.
For example, if one uses , r(t)=(costcos2t,costsin2t,sint) r ( t ) = ( cos t cos 2 t , cos t sin 2 t , sin t ) , one obtains a ruled surface that contains the Möbius strip.
–The Gaussian curvature on a ruled regular surface is everywhere non-positive.
–The only ruled minimal surfaces are the plane and helicoid (Catalan 1842, do Carmo 1986).
Examples: Cylinders, Cones, 1-sheeted Hyperboloid, Hyperbolic Paraboloid, Helicoid, Right Conoid, Whitney Umbrella. In other sections: Double Helix, M o¨ o ¨ bius Strip.Doubly Ruled Surface:
–A surface that contains two families of ruling.
–A surface is doubly ruled if through every one of its points there are two distinct lines that lie on the surface.
The only three doubly ruled surfaces are the plane (the only surface which contains at least 3 distinct lines), hyperbolic paraboloid, and single-sheeted hyperboloid.Developable Surface:
–Smooth ruled surface with zero Gaussian curvature
–A surface that can be flattened onto a plane without distortion (tearing or stretching).
In three dimensions all developable surfaces are ruled surfaces (but not vice versa). If a developable surface lies in three-dimensional Euclidean space, and is complete, then it is necessarily ruled, but the converse is not always true. For instance, the cylinder and cone are developable, but the general hyperboloid of one sheet is not. There are developable surfaces embedded in four dimensions which are however not ruled (Hilbert & Cohn-Vossen 1952, pp. 341–342).
Examples: cone, cylinder, elliptic cone, hyperbolic cylinder, and plane.Saddle surface: The Gauss curvature at any point is non-positive, meaning it is impossible to cut off a crust by any plane. For a twice continuously-differentiable surface to be a saddle surface it is necessary and sufficient that at each point of the surface its Gaussian curvature is non-positive. A surface for which all its points are saddle points (cf. Saddle point) is a saddle surface.
Embeddedness: A surface is called embedded if it has no self-intersections. This poses strong restrictions on minimal surfaces.
Hyperboloid (双曲面)


A hyperboloid of revolution is a surface that may be generated by rotating a hyperbola around one of its principal axes. More generally, a hyperboloid centered at v is defined by the equation
where A is a matrix and x, v are vectors. The eigenvectors of A define the principal directions of the hyperboloid and the eigenvalues of A are the reciprocals of the squares of the semi-axes: 1/a2 1 / a 2 , 1/b2 1 / b 2 and 1/c2 1 / c 2 . The one-sheet hyperboloid has two positive eigenvalues and one negative eigenvalue. The two-sheet hyperboloid has one positive eigenvalue and two negative eigenvalues ( Why?).
| Hyperboloid type | image | property | application |
|---|---|---|---|
| Elliptic Hyperboloid or two-sheet hyperboloid
x2a2+y2b2−z2c2=−1
x
2
a
2
+
y
2
b
2
−
z
2
c
2
=
−
1
. Parametrized as:
v∈[0,∞)
v
∈
[
0
,
∞
)
xyz=asinhvcosθ=bsinhvsinθ=±ccoshv.
x
=
a
sinh
v
cos
θ
y
=
b
sinh
v
sin
θ
z
=
±
c
cosh
v
.
|  | Positive Gaussian curvature at every point. | |
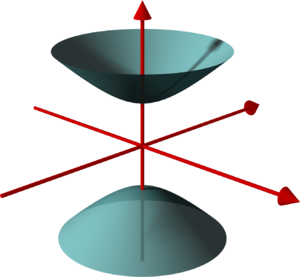
| Hyperbolic Hyperboloid or one-sheet hyperboloid
x2a2+y2b2−z2c2=1
x
2
a
2
+
y
2
b
2
−
z
2
c
2
=
1
Parametrized as:
v∈(−∞,∞)
v
∈
(
−
∞
,
∞
)
xyz=acoshvcosθ=bcoshvsinθ=csinhv.
x
=
a
cosh
v
cos
θ
y
=
b
cosh
v
sin
θ
z
=
c
sinh
v
.
|   | Negative Gaussian curvature at every point. Doubly ruled surface |   Canton Tower Canton Tower |
| Cone
x2a2+y2b2−z2c2=0
x
2
a
2
+
y
2
b
2
−
z
2
c
2
=
0
Parametrized as:
v∈(−∞,∞)
v
∈
(
−
∞
,
∞
)
xyz=asinhvcosθ=bsinhvsinθ=csinhv.
x
=
a
sinh
v
cos
θ
y
=
b
sinh
v
sin
θ
z
=
c
sinh
v
.
|  |
Paraboloid (抛物面)
| Paraboloid type | image | property | application |
|---|---|---|---|
| Elliptic Paraboloid (椭圆抛物面) z=x2a2+y2b2 z = x 2 a 2 + y 2 b 2 . Parametrized as x=u−−√cosv,y=u−−√sinv,z=u. x = u cos v , y = u sin v , z = u . |   |   parabolic antennas parabolic antennas | |
| Hyperbolic Paraboloid (双曲抛物面) z=y2b2−x2a2 z = y 2 b 2 − x 2 a 2 (left image) or alternatively, z=xy z = x y (right image). Parametrized as x(u,v)=u,y(u,v)=v,z(u,v)=uv. x ( u , v ) = u , y ( u , v ) = v , z ( u , v ) = u v . |  Two ways of parameterization. Two ways of parameterization. | Doubly ruled surface, not developable (smooth surface with zero Gaussian curvature), Saddle surface |  |
Minimal Surfaces
Catenoid (悬链面) & Helicoid (螺旋面)
| type | image | property | application |
|---|---|---|---|
| Catenoid x1(u,v)=(coshvcosu,coshvsinu,v),(u,v)∈U:=(0,2π)×R x 1 ( u , v ) = ( cosh v cos u , cosh v sin u , v ) , ( u , v ) ∈ U := ( 0 , 2 π ) × R |   A catenoid obtained from the rotation of a catenary. A catenoid obtained from the rotation of a catenary. | The only minimal surface of revolution. |  |
| Helicoid: x2(u,v)=(−sinhvsinu,sinhvcosu,−u), (u,v)∈U x 2 ( u , v ) = ( − sinh v sin u , sinh v cos u , − u ) , ( u , v ) ∈ U |  | The only ruled minimal surface. | |
| The surface
Sθ
S
θ
for some
θ∈R
θ
∈
R
(Linear combination of catenoid and helicoid):
yθ(u,v)=(cosθ)x1(u,v)+(sinθ)x2(u,v), (u,v)∈U
y
θ
(
u
,
v
)
=
(
cos
θ
)
x
1
(
u
,
v
)
+
(
sin
θ
)
x
2
(
u
,
v
)
,
(
u
,
v
)
∈
U
|  | ||
| Various θ θ for the surface Sθ S θ |
| θ=0 θ = 0 | θ=π/4 θ = π / 4 | θ=π/2 θ = π / 2 |
|---|---|---|
 |  |  |
| θ=3π/4 θ = 3 π / 4 | θ=π θ = π | θ=5π/4 θ = 5 π / 4 |
 |  |  |
| θ=3π/2 θ = 3 π / 2 | θ=7π/4 θ = 7 π / 4 | θ=2π θ = 2 π |
 |  |  |
| Animation 1 | Animation 2 |
|---|---|
 |  |
Animation Source:
1. http://www.foundalis.com/mat/helicoid.htm
2. https://en.wikipedia.org/wiki/Helicoid
Catenoid-Helicoid Associate Family
The intermediate family of surfaces between the catenoid and the helicoid is called the associate family. The associate family of a minimal surface consists of a deformation by isometric minimal surfaces.
What does the Associate Family mean?
For a 2D worm living in the surface of this family of minimal surface, it is unable to know how the space it is living in is embedded in 3D space. The interior of a catenoid can be evolved without much effort to the exterior, upon an isometry (or congruent transformation).
User Interface Animation and brief introduction: 3DXM Minimal Surface Gallery
 Source:
http://www.indiana.edu/~minimal/maze/index.html
Source:
http://www.indiana.edu/~minimal/maze/index.html
Ref:
1. http://virtualmathmuseum.org/docs/RuledSurfaces.pdf
2. http://3d-xplormath.org/
3. http://virtualmathmuseum.org/docs/Helicoid-Catenoid.pdf
4. Matthias Weber’s Virtual Minimal Surface Museum (Abundant materials for Minimal Surfaces)
5. A beautiful gallery of Minimal surfaces
*Cross-entropy method
1. http://iew3.technion.ac.il/CE/files/Misc/tutorial.pdf
2. http://iew3.technion.ac.il/CE/
























 807
807

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








