这篇文章是对博客http://blog.csdn.net/cyh_24/article/details/50359055内容的搬运,个人感觉作者写得很好,所以自己想从头到尾“誊写”一遍,以便理解透彻。谢谢作者的辛苦总结~
PS:因为实习,将近3个月没有再写论文笔记了,该篇算是一个开头,后边一定要保证每周一篇阅读笔记。
该篇blog主要内容如下:
1. LR的数学理论
2. LR的求解推导过程
3. LR的正则化(正则化的概念)
4. logistic /linear regression的比较
5. LR和ME(最大熵)的关系
6. LR的并行化
首先需要清楚的是,LR(logistic regression)虽然是回归模型,但却是经典的分类方法。
我们分开来看逻辑斯蒂和回归这两个概念。
逻辑斯蒂
逻辑斯蒂是一种变量的分布方式,和常见的指数分布、高斯分布等类似,它也有自己的概率分布函数和概率密度函数,如下:

他们的图形如下图所示:
回归
我们为什说逻辑斯蒂模型是个分类模型而不是回归模型?这个回归到底是怎么回事呢?下边就来解决这一疑惑。
首先我们来看最简单的二项logstic regression模型,它是由条件概率分布来表示,即:
此处引入几个简单的数学概念:
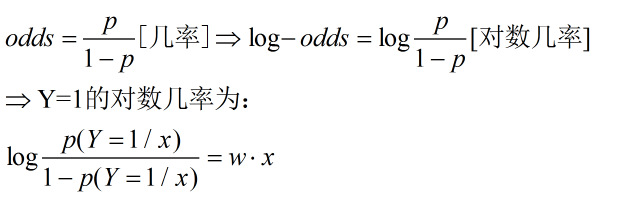
可以看到,Y=1的对数几率是输入x的线性函数,同时我们看到:
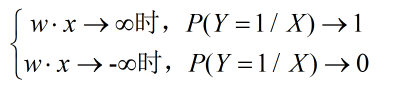
即输出Y的取值概率是由输入x的线性函数决定的的,回归也就体现在这里。
接下来就是第二个问题:LR模型的求解。
模型求解也就是模型参数的估计。因为逻辑斯蒂回归是典型的统计机器学习方法,所以经常用最大似然估计的方法。
此处需要注意的是,我们经常见到的表述是目标函数的最小化,那么为什么这里的是对似然的最大化呢?

所以似然函数的最大化等价于损失函数的最小化。
解开了第一个疑惑,接下来我们就可以利用最大似然估计来求解模型参数啦。
参数求解常用的方法是梯度下降法(GD)。下边是具体算法实现过程。

当模型参数很多,而我们可用的数据非常少时,极易出现过拟合的问题。为此,就引入了正则化。 其目的是使得参数空间受到一定的限制。
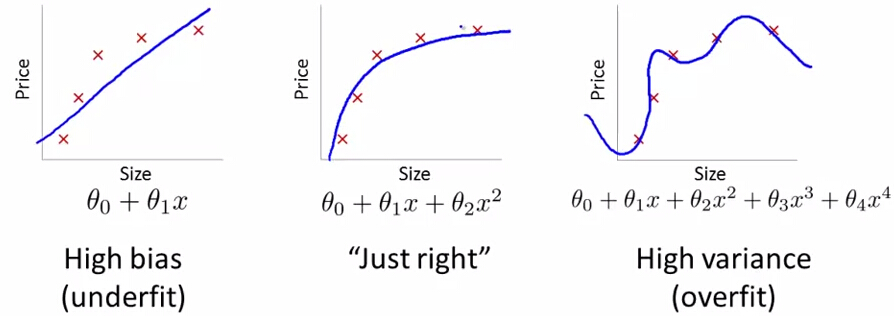
上图可以更直观的理解欠拟合和过拟合问题。为了避免这种情况,一般都是在目标函数里加上正则项。即:
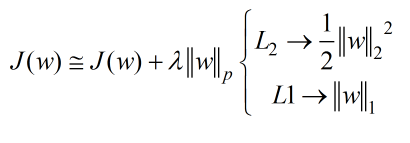
首先介绍L2正则化,它也被称为权重延迟或脊回归。此时的目标函数如下:
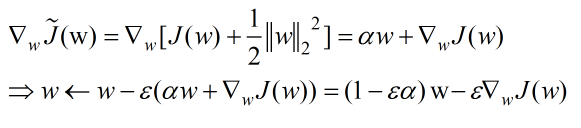
可以看到,正则项的加入改变了参数的学习规则,它在参数的每一步更新中都新增了一个系数参量。
接下来我们来看看L1正则化:
这两个不同的的正则化方法对参数最优化存在着怎样不同的影响呢?
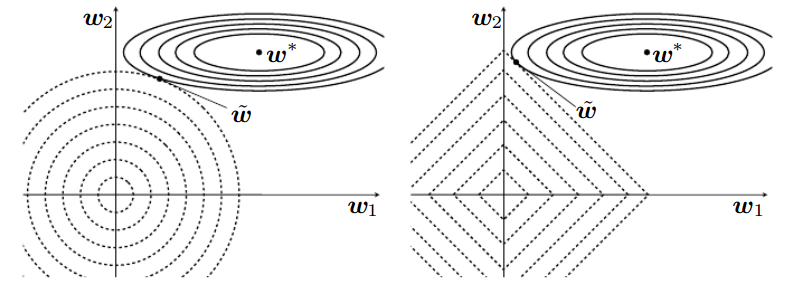
上图分别是L2和L1正则化对应的图,反应的是它们对参数优化的影响。给我们的直观感受是L2对参数的正则更加的平滑,即它限制了参数空间,但对参数的影响是平滑的,不像L1那样,直接使得某些参数的取值为0.
总结起来就是:L1会引入稀疏性,而L2会充分利用更多的特征。
好。。。(有些累,先歇会儿~)
上边说到,逻辑斯蒂回归是分类算法,即根据现有的数据集对分类边界线建立回归公式,寻求最佳的边界直线/曲线的拟合。那它和线性回归存在着哪些的不同呢?
顾名思义,线性回归是假设输入X和输出Y之间满足的是传统的线性关系Y=WX,而在逻辑斯蒂回归中,假设输入和输出的关系满足逻辑斯蒂函数,即:
在使用线性回归时有几个限制:
- 不应该使用这种方法来预测和建立模型时所使用的数据值相关差甚远的值。
- 避免模型中自变量之间有较高的相关性。
- 对噪声数据敏感。
- 一般假设误差变量( error variances 或residuals)服从均值为0的正态分布。
而逻辑斯蒂回归在这些问题上能得到较好的解决。
还有两个大问题亟待解决,今儿实在扛不住了,休息会儿。本周前将该专题写完。嗯嗯。。。
参考资料:
【1】http://blog.csdn.net/cyh_24/article/details/50359055
【2】http://www.cnblogs.com/zhangchaoyang/articles/2640700.html
【3】统计机器学习(李航)
【4】机器学习实战(Peter Harrington)









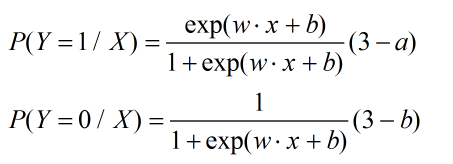

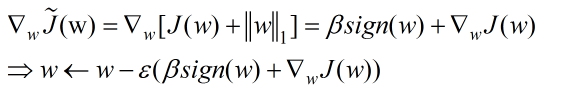
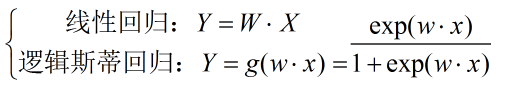














 89
89

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








