我们先从LDA的起源说起。
根据Blei大神在论文上的描述看来,最初是由于tf-idf(term frequency–inverse document frequency)在IR(信息检)中的应用,使人们认识到这样用数字表示的feature竟然可以很好的区分文档,而且还可以起到降维的作用。(tf-idf用每个单词对应的词频-倒排频率来表示单词,相对原来的文档,长度减少了)。于是人们就开始思考,是不是可以对这种方法进行扩展,让它可以更好的降维那?于是LSI便产生了,但是LSI是用矩阵的奇异值分解来做的,先不管他的计算复不复杂,首先他就很难理解,你把文档分成两个矩阵,那这两个矩阵都是什么东西啊,你分开来干什么(当然是降维了),为什么可以这样分那。所以有人就建立了一个生成模型来形象的表示--PLSI。
其实PLSI和LSI说的是同一件事情,不过人家高明多了,你看,中间这个你没有办法解释的东西,是主题。这个主题到底是个什么东西那,这里涉及到一个“bag of word”的性质,什么是“bag of word”那,就是你看,一篇文章里有好多个单词,你不要考略单词之间的顺序了,你就认为他们其实是乱七八糟堆在一个袋子里的词,当然这个袋子就是一个文档。
不考略顺序可不是不考略他们之间的关系,他们之间的关系当然也要考虑,你想,you 和 are这两个词是不是经常在一起出现,但是偶尔are也会和we 在一起,那么这样的关系怎么表示那?其实我们看到这样朝三暮四的变量的时候,本能的就会想起混合模型了,没错,还就是混合模型。Finetti大神说了,你这种随便堆起来的变量,其实可以看成是一个无限混合的混合模型的样本。是不是好像知道了点什么,好像还差点火候,我们把这样的混合模型写出来
还是不太清楚,那好换几个参数
这样是不是就很清楚了,这不就是上面的那个图么,恩恩,原来这个主题指的就是你这w到底是从那个混合分布里采样的样本啊,仔细一想,这不就是这么一回事吗,你看我们想确定文章的主题,在从主题选择单词来表达这个主题,这真是非常自然的事情啊。
拿着PLSi模型了,我们很高兴,拿他去解决问题吧,恩恩,降维的任务完成了,虽然参数有点多(因为对于数据集中的每一个文档,都必须表示出他的各个主题所占的比列),参数多点就多点吧,我们忍忍。这时候数据库更新了,新来了一篇文章,这文章我们没见过,他的主体比例我们完全不知道,这样我们没办法搞。这样是不行的,这说明我们这个模型有缺陷,那好,改改吧,怎么改那?
你不是说新来的文章不知道主体比例没法搞吗,我们就改改模型让他能够产生这个主题的比例,怎么改?我们给主题加个分布让模型可以产生主题不就行了吗?但是这个分布并不是乱加的,那你要是加个均匀分布可以吗?也可以,不过这样模型可能就不太好了。那么blei大神给我们加的是什么分布那?dirichlet!恩恩,精髓啊。当然,这也不是他随便选的,dirichlet不就是multinomial的先验吗?这样一看,非常合情合理,大神就是大神。然后我们的模型变成什么样了,先看看公式
这里的p(w)是单词w在数据库中出现的概率。
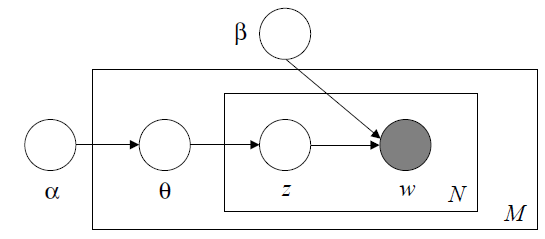
这个公式一看,清清楚楚,单词不是已经不考虑顺序了吗,那么主题不也就不考虑顺序了吗?这不就是"bag of topic“么,根据finetti大神的发现,这主题不也可以表示成混合分布吗?一篇文章主题确定了,文章不就确定了么?那么这个混合分布不就是我们要找的先验吗。这样,以个模型就出来了,我们把模型的贝叶斯图画出来
恩恩,我们的LDA模型不就出来么?










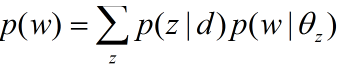
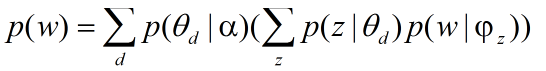














 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








