对于圆弧拟合算法是多种多样的,比较常规的是:最小二乘法圆弧拟合和双圆弧拟合。就工控领域而言,这里提出一种过起点/终点的误差可控的圆弧拟合算法。本算法基于最小二乘法圆弧拟合的基础上,实现误差可控,适用于连续顺序输出的轨迹拟合。
算法如下:
圆的标准方程:x^2+y^2+ax+by+c=0 (1)
起点坐标:(x0,y0) 终点坐标:(xn,yn)
将起点和终点坐标带入(1)式:
x0^2+y0^2+ax0+by0+c=0 (2)
xn^2+yn^2+axn+byn+c=0 (3)
(2) - (3) 可得:
(x0^2-xn^2)+(y0^2-yn^2)+a(x0-xn)+b(y0-yn)=0
当(y0-yn) != 0时,有:
b=[(x0^2-xn^2)+(y0^2-yn^2)+a(x0-yn)] / (yn-y0) (4)
( (2)*yn - (3)*y0 )可得:
(yn*x0^2-y0*xn^2)+(yn*y0^2-y0*yn^2)+a(x0*yn-xn*y0)+c(yn-y0)=0
当(yn-y0) != 0时,有:
c=[(yn*x0^2-y0*xn^2)+(yn*y0^2-y0*yn^2)+a(x0*yn-xn*y0)] / (y0-yn) (5)
令 D = [(x0^2-xn^2)+(y0^2-yn^2)]/(yn-y0)
E = (x0-xn)/(yn-y0)
F = [(yn*x0^2-y0*xn^2)+(yn*y0^2-y0*yn^2)]/(y0-yn)
G = (x0*yn-xn*y0)/(y0-yn)
则 b = D+a*E (6)
c = F+a*G (7)
令 Q(a,b,c) = ∑[(xi^2+yi^2+a*xi+b*yi+c)^2] (8)
将(6)和(7)代入(8)可得:
Q(a,b,c) = ∑[(xi^2+yi^2+a*xi+(D+a*E)*yi+(F+a*G))^2] (9)
让Q(a,b,c)对a求偏导可得:
∂ Q(a,b,c)/∂a = 2*∑[(xi^2+yi^2+a*xi+(D+a*E)yi+(F+a*G))(xi+E*yi+G)]
根据最小二乘法原理可知:∂ Q(a,b,c)/∂a = 0
即:
∑[(xi^2+yi^2+a*xi+(D+a*E)yi+(F+a*G))(xi+E*yi+G)] = 0
化简可得:
∑[(xi^2+yi^2+D*yi+F)(xi+E*yi+G)]+∑[a(xi+E*yi+G)^2] = 0 (10)
当∑[(xi+E*yi+G)^2] !=0时,由(10)式可得:
a = -∑[(xi^2+yi^2+D*yi+F)*(xi+E*yi+G)]/∑[(xi+E*yi+G)^2]
令Hi = xi+E*yi+G , J = ∑[(xi^2+yi^2+Dyi+F)*Hi]
则:a = - J/(∑Hi^2) (11)
整理后的拟合算法为:
圆弧方程:x^2+y^2+ax+by+c=0
D = [(x0^2-xn^2)+(y0^2-yn^2)]/(yn-y0)
E = (x0-xn)/(yn-y0)
F = [(yn*x0^2-y0*xn^2)+(yn*y0^2-y0*yn^2)]/(y0-yn)
G = (x0*yn-xn*y0)/(y0-yn)
Hi = xi+E*yi+G
J = ∑[(xi^2+yi^2+Dyi+F)*Hi]
a = - J/(∑Hi^2)
b = D+a*E
c = F+a*G
由上可知,当(yn-y0) != 0时,可先行算出a的值,再根据式(6)、(7)可算出b和c,最终算得拟合的圆弧方程。
当(yn-y0) = 0时,(2) - (3) 有:
(x0^2-xn^2)+(y0^2-yn^2)+a(x0-xn) = 0 (12)
在(12)中,当(x0-xn) != 0 时有:
a = [(x0^2-xn^2)+(y0^2-yn^2)]/(xn-x0) (13)
由(8)式和最小二乘法原理可得:
∂ Q(a,b,c)/∂b = 0
∂ Q(a,b,c)/∂c = 0
即:
∂ Q(a,b,c)/∂b = ∑[(xi^2+yi^2+a*xi+b*yi+c)*yi] = 0 (14)
∂ Q(a,b,c)/∂c = ∑(xi^2+yi^2+a*xi+b*yi+c) = 0 (15)
由(15)可得:
c = - [ ∑(xi^2+yi^2+a*xi+b*yi) ]/n (16)
将(16)代入(14)可求得:
当∑(yi^2 * (1/n - 1)) != 0时,有:
b = [ ∑(xi^2+yi^2+a*xi)(1-1/n)*yi ] / [ ∑(yi^2 (1/n - 1)) ] (17)
令:D = xi^2+yi^2+a*xi
E = (1-1/n)*yi
F = E*yi
则有:
b = ∑(D*E) / ∑(E*F)
C = - ∑(D+b*yi) / n
整理后的拟合算法为:
圆弧方程:x^2+y^2+ax+by+c=0
a = [(x0^2-xn^2)+(y0^2-yn^2)]/(xn-x0)
D = xi^2+yi^2+a*xi
E = (1-1/n)*yi
F = E*yi
b = ∑(D*E) / ∑(E*F)
C = - ∑(D+b*yi) / n
由上可知,当(yn-y0) = 0时,可先行算出a和b的值,再根据式(16)可算出c,最终算得拟合的圆弧方程。
如需要计算圆心坐标和半径可根据以下公式计算:
A = - a / 2
B = - b / 2
R =√(a*a+b*b-4*c) / 2
对于工控行业而言,最重要的是误差可控,故对圆弧拟合的结果进行误差统计,即:将每个离散点的坐标输出误差公式:
√| (xi - A)^2 + (yi - B)^2 - R | > max_dev
其中max_dev为最小允许拟合误差。当拟合误差超过最小允许拟合误差时,需减少一个拟合离散点,重新进行拟合运算,直至误差在允许范围内,或者离散点总数少于3个。
注意:当待拟合线段长度过长时,则该线段的中点也应代入误差公式进行误差统计,以防止误差过大。
下面为圆弧拟合算法的C语言实现:
typedef struct{
float x;
float y;
}COORDINATE;
typedef enum{
LINE,
ARC,
}FIT_TYPE;
typedef struct{
FIT_TYPE type;//拟合结果
float st_x;//起点坐标x
float st_y;//起点坐标y
float ed_x;//终点坐标x
float ed_y;//终点坐标y
float arc_x;//圆心坐标x
float arc_y;//圆心坐标y
float R;
}CIRCLE;
#define coordinate_SIZE (20u)//缓冲器大小
#define MAX_DEV (0.02F)//最大允许拟合误差
uint8_t cur_idx= 0;//记录当前拟合缓冲器中的索引
uint8_t first_idx = 0;//记录前拟合缓冲器中的第一段索引
uint8_t poinsum = 0;
COORDINATE coordinate[coordinate_SIZE];
static uint8_t Next_coordinate(uint8_t idx)
{//环形缓冲器向前计数
idx++;
if (idx == coordinate_SIZE) { idx = 0; }
return idx;
}
static uint8_t Next_n_coordinate(uint8_t idx, uint8_t n)
{
uint8_t i = 0;
for(;i<n;i++){
idx = Next_coordinate(idx);
}
return idx;
}
static uint8_t Prev_coordinate(uint8_t idx)
{//环形缓冲器向后计数
if (idx == 0) { idx = coordinate_SIZE; }
idx--;
return idx;
}
static bool least_square_method_circle_fitting(uint8_t Idx , uint8_t num, CIRCLE *arc)
{
uint8_t i = 0;
uint8_t cur_idx = Idx;
uint8_t next_idx = Next_coordinate(Idx);
float a,b,c,D,E,F,G,Hi,J,K;
float A,B,R;
float x0,y0,xn,yn;
float x0_pow,y0_pow,xn_pow,yn_pow;
if(num<3){//因为是线段,故最少点数不少于2个
arc->type = LINE;
arc->st_x= coordinate[Idx].x;
arc->st_y= coordinate[Idx].y;
arc->ed_x= coordinate[next_idx].x;
arc->ed_y= coordinate[next_idx].y;
return ture;
}
for(i=0;i<num;i++){
K = coordinate[next_idx].x - coordinate[cur_idx].x;
if(K!=(0.0f)){
K=(coordinate[next_idx].y - coordinate[cur_idx].y)/K;
break;
}
else {
cur_idx = next_idx;
next_idx = Next_coordinate(next_idx );
}
if(i == (num-1)){//所有点共线,且与Y轴平行
arc->type = LINE;
arc->st_x= coordinate[Idx].x;
arc->st_y= coordinate[Idx].y;
arc->ed_x= coordinate[next_idx].x;
arc->ed_y= coordinate[next_idx].y;
return ture;
}
}
cur_idx = Idx;
next_idx = Next_coordinate(Idx);
if(i==0){
for(i=1;i<num;i++){
cur_idx = Next_coordinate(cur_idx);
next_idx = Next_coordinate(cur_idx);
D = coordinate[next_idx].y - coordinate[cur_idx].y;
D /= coordinate[next_idx].x - coordinate[cur_idx].x;
if(K != D) break;
if(i == (num-1)){//所有点共线,且不与Y轴平行
arc->type = LINE;
arc->st_x= coordinate[Idx].x;
arc->st_y= coordinate[Idx].y;
arc->ed_x= coordinate[next_idx].x;
arc->ed_y= coordinate[next_idx].y;
return ture;
}
}
}
cur_idx = Idx;
x0 = coordinate[cur_idx].x;
y0 = coordinate[cur_idx].y;
xn = coordinate[Next_n_coordinate(cur_idx, num-1)].x;
yn = coordinate[Next_n_coordinate(cur_idx, num-1)].y;
x0_pow = x0*x0;
y0_pow = y0*y0;
xn_pow = xn*xn;
yn_pow = yn*yn;
if(y0 != yn){
D = ((x0_pow-xn_pow)+(y0_pow-yn_pow))/(yn - y0);
E = (x0 - xn)/(yn - y0);
F = (((yn*x0_pow) - y0*xn_pow)+((yn*y0_pow)-(y0*yn_pow)))/(y0 - yn);
G = ((x0*yn) - (xn*y0))/(y0 - yn);
for(i=0;i<num;i++){
Hi = (coordinate[cur_idx].x + E*coordinate[cur_idx].y + G);
Hi_pow += Hi*Hi;
J += ((coordinate[cur_idx].x*coordinate[cur_idx].x + coordinate[cur_idx].y*coordinate[cur_idx].y + D*coordinate[cur_idx].y + F)*Hi);
cur_idx = Next_coordinate(cur_idx);
}
a = -1*(J/Hi_pow);
b = D + a*E;
c = F + a*G;
}else{
a = ((x0_pow-xn_pow)+(y0_pow-yn_pow))/(xn - x0);
G = 0;
Hi = 0;
for(i=0;i<num;i++){
D = pow(coordinate[cur_idx].x,2)+pow(coordinate[cur_idx].y,2)+a*coordinate[cur_idx].x;
E = (1-num)*coordinate[cur_idx].y;
F = E*coordinate[cur_idx].y;
G += D*E;
Hi+= E*f;
cur_idx = Next_coordinate(cur_idx);
}
b = G/Hi;
cur_idx = Idx;
D = 0;
E = 0;
for(i=0;i<num;i++){
D += pow(coordinate[cur_idx].x,2)+pow(coordinate[cur_idx].y,2)+a*coordinate[cur_idx].x;
E += b*coordinate[cur_idx].y;
}
c = -(D+E)/num;
}
cur_idx = Next_n_coordinate(Idx, num-1)
arc->type = ARC;
arc->st_x= coordinate[Idx].x;
arc->st_y= coordinate[Idx].y;
arc->ed_x= coordinate[cur_idx ].x;
arc->ed_y= coordinate[cur_idx ].y;
arc->arc_x = a/(-2);
arc->arc_y = b/(-2);
arc->R = sqrt(a*a+b*b-4*c)/2;
return check_deviation(Idx , num, arc);//误差检测
}
//误差检测
static bool check_deviation(uint8_t Idx , uint8_t num, CIRCLE *arc)
{
uint8_t i;
uint8_t cur_idx = Idx ;
uint8_t dec_idx = Idx ;
float dev = 0;
float x,y;
for(i=1; i<num; i++){
cur_idx = Next_Arc_Fit_Buff(cur_idx );
dev = pow(coordinate[cur_idx].x-arc->arc_x,2);
dev += pow(coordinate[cur_idx].y-arc->arc_y,2);
dev =sqrt(fabs(dev));
if(dev > MAX_DEV) retrun false;
x = (coordinate[cur_idx].x + coordinate[dec_idx ].x)/2.0;
y = (coordinate[cur_idx].x + coordinate[dec_idx ].x)/2.0;
dev = pow(x*x-arc->arc_x,2);
dev += pow(y*y-arc->arc_y,2);
dev =sqrt(fabs(dev));
if(dev > MAX_DEV) retrun false;
dec_idx = cur_idx ;
}
return true;
}
//圆弧拟合函数
//每次输入一个坐标,当数据结束时应使isFinish = true, arc为拟合结果,sursum为剩余的拟合点数
bool Arc_Fitting(float x, float y, bool isFinish, CIRCLE *arc, uint8_t *sursum)
{
coordinate[cur_num].x = x;
coordinate[cur_num].y = y;
bool res = false;
uint8_t sum = 0;
poinsum++;
cur_idx= Next_coordinate(cur_num);
if(cur_idx== first_idx || isFinish == ture){
res = least_square_method_circle_fitting(first_idx, poinsum, arc);
sum = poinsum;
while(res != true && sum >= 2) {
sum--;
res = least_square_method_circle_fitting(first_idx, sum, arc);
}
first_idx = Next_n_coordinate(first_idx,sum);
*sursum = poinsum - sum ;
return res;
}else return false;
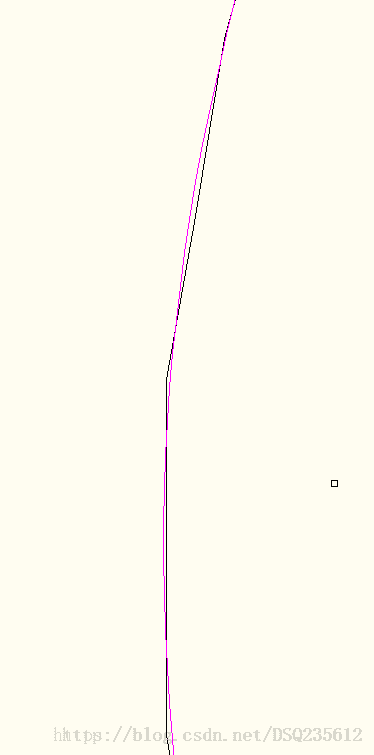
}拟合结果如下:
放大后观察1:
放大后观察2:
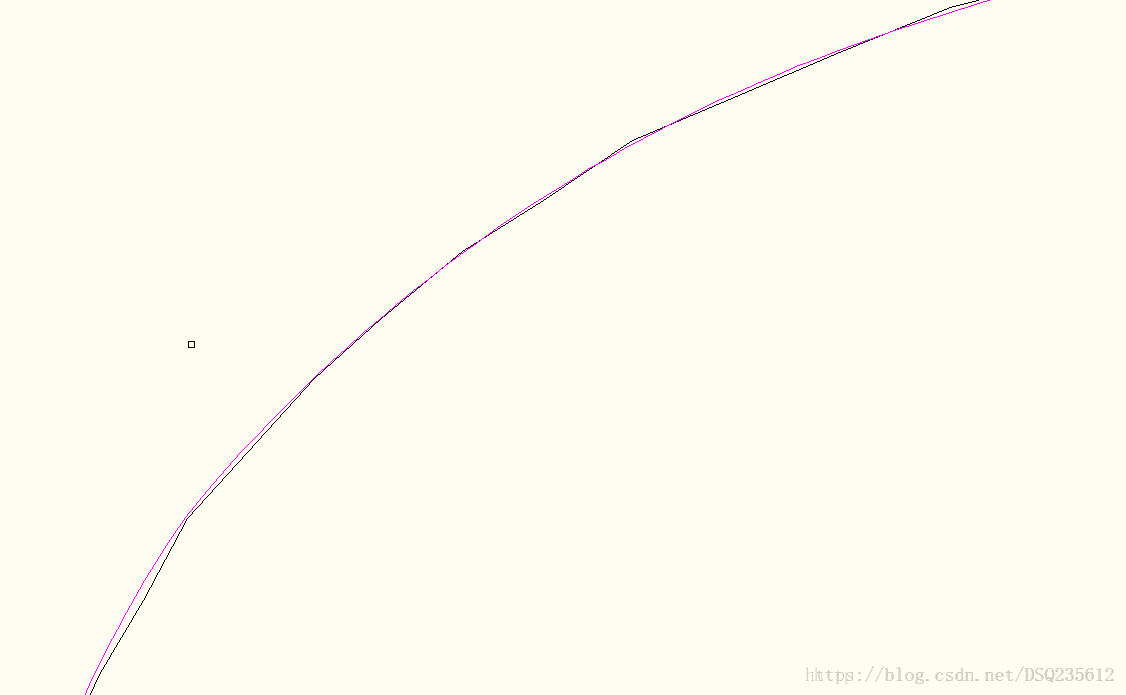
由上可看出拟合效果相当可观,当然仍有许多考虑不全的地方,在实际项目应用中,根据项目需求改变算法计算的复杂度,和节省所占的堆栈空间。后期将提出一种圆弧方向的判别方法,以及对双圆弧拟合进行总结,采用双圆弧拟合将更大程度的圆滑轨迹,减少设备抖动。
结语:初来乍到,仍有许多不足的地方,希望各位看官勿喷!








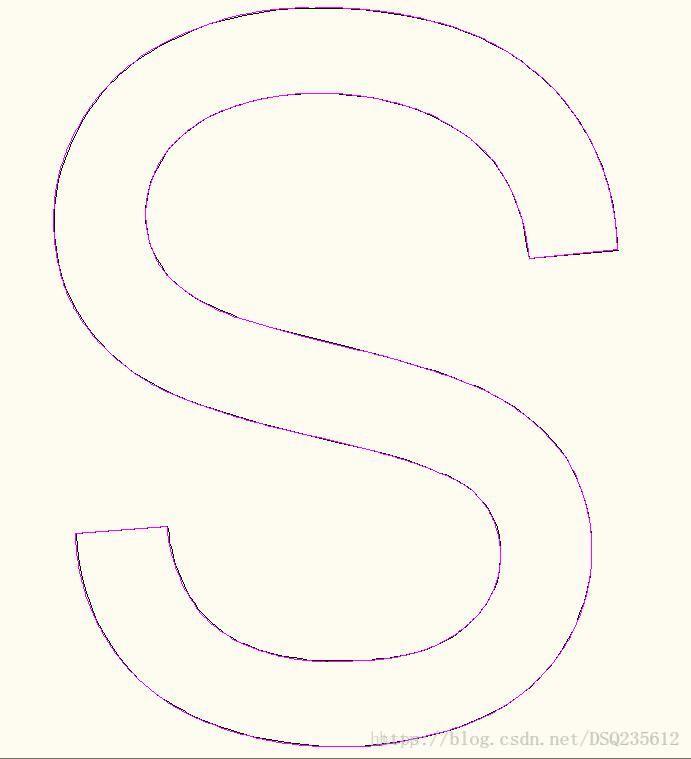













 3146
3146











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








