快速理解
[说明]:此节使用通俗语言进行扩散模型的总体概述,用词较为冗杂,某些概念为简易性做了些许牺牲,可能略有偏颇。深入理解请继续阅读后续章节,概念定义也以后续章节为准。
扩散模型是一类生成模型,在训练此类模型时,它可以被分为两个阶段,分别称为扩散阶段和逆扩散阶段。扩散阶段主要对训练数据样本
x
0
x_0
x0不断添加高斯噪声,在重复足够的次数(一般表示为
T
T
T步)后,此数据样本变为各项独立的高斯样本
x
T
x_T
xT,这与VAE中的编码过程神似。逆扩散过程是主要是对一个高斯样本
x
T
x_T
xT不断的进行减高斯噪声的操作,在
T
T
T步后将获得一个符合训练数据分布的样本
x
0
′
x'_0
x0′,这与VAE中解码神似。如果此过程被确定,则在推理阶段我们能使用任意的高斯样本逆扩散为一个符合训练数据分布的样本(这达到了生成模型的目的)。此训练过程可以用下图表示:
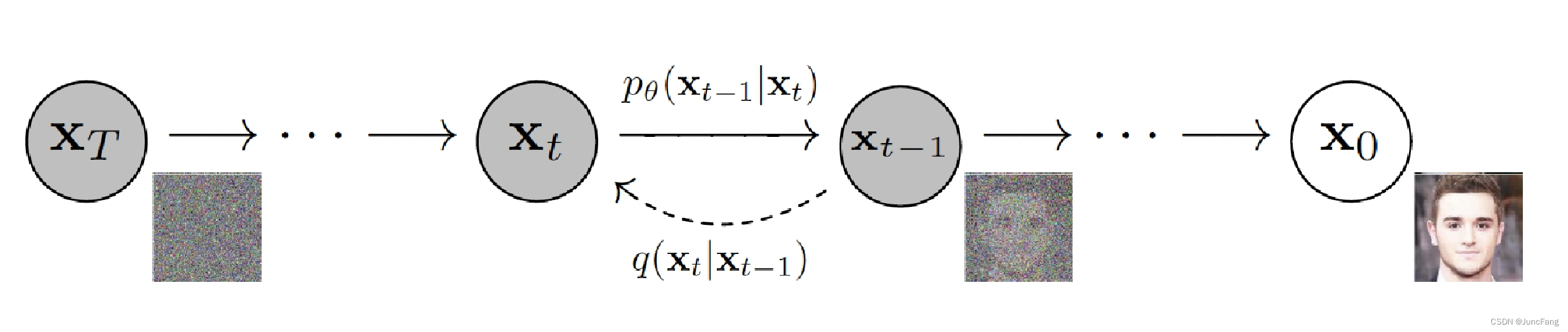
在训练过程,我们将确定一个加入噪声的策略,这被称作nois_schedule,由于高斯噪声的主要影响参数为均值(
μ
\mu
μ)和标准差(
σ
\sigma
σ),此策略主要决定的是当前步数(
t
t
t)时,加入高斯噪声的均值和标准差。在此策略和训练样本
x
0
x_0
x0被确定的情况下,我们的扩散过程能被逐步推出。所以更重要的是逆扩散过程。
在逆扩散过程中,需要做的是逐步减高斯噪声,如果我们将其定义为直接减去扩散过程中加入的那个高斯噪声则在经过
T
T
T步后就能还原数据样本
x
0
x_0
x0。但这样的定义将毫无意义,因为在推理阶段(从随机高斯样本逆扩散到样本数据),我们并没有加噪声策略的记录,也就无法获得减噪声的策略,逆扩散过程将无法进行。
所以,在训练阶段的逆扩散过程,我们需要使用神经网络来预测这个减噪声的策略,当此策略满足训练集样本的极大似然估计的时侯,推理阶段就可使用此神经网络来生成减噪声策略,从而用随机高斯样本生成符合训练集分布的生成样本。
神经网络损失函数的定义至关重要。在训练过程,由于已知样本数据
x
0
x_0
x0和加噪声策略,我们能轻易求出
x
T
x_T
xT和
x
T
−
1
x_{T-1}
xT−1。所以神经网络可以设定为接收已知的信息
x
T
x_T
xT和
T
T
T为输入,预测其减噪声后的结果
x
T
−
1
′
x'_{T-1}
xT−1′。已知预测值
x
T
−
1
′
x'_{T-1}
xT−1′和真实值
x
T
−
1
x_{T-1}
xT−1,损失函数则呼之欲出。(注意,此处不具有数学严谨性,只为描述神经网络的建模想法)
数学基础
[说明]:下章节开始介绍扩散模型数学原理,对此数学基础的掌握必不可少。为简单起见,读者可不深究此节相关内容,但需要在阅读下节时实时翻阅,以作为推到的理论基础。
高斯分布表示 (数1)
符号表示:
N
(
μ
,
σ
2
)
N(\mu, \sigma^2)
N(μ,σ2)。 其中
μ
\mu
μ为均值,
σ
\sigma
σ为标准差。
概率密度函数:
f
(
x
)
=
1
2
π
σ
e
x
p
(
−
1
2
(
x
−
μ
)
2
σ
2
)
=
1
2
π
σ
e
x
p
(
−
1
2
(
1
σ
2
x
2
−
2
μ
σ
2
x
+
μ
2
σ
2
)
)
f(x) = \frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2})= \frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{1}{2}(\frac{1}{\sigma^2}x^2-\frac{2\mu}{\sigma^2}x+\frac{\mu^2}{\sigma^2}))
f(x)=2πσ1exp(−21σ2(x−μ)2)=2πσ1exp(−21(σ21x2−σ22μx+σ2μ2))
高斯分布线性叠加 (数2)
两个高斯分布
X
∼
N
(
μ
1
,
σ
1
2
)
X\sim N(\mu_1, \sigma^2_1)
X∼N(μ1,σ12),
Y
∼
N
(
μ
2
,
σ
2
2
)
Y\sim N(\mu_2, \sigma^2_2)
Y∼N(μ2,σ22)进行线性组合仍然为高斯分布,表示为:
a
X
+
b
Y
∼
N
(
a
μ
1
+
b
μ
2
,
a
2
σ
1
2
+
b
2
σ
2
2
)
aX+ bY \sim N(a\mu_1+b\mu_2, a^2\sigma^2_1+b^2\sigma^2_2)
aX+bY∼N(aμ1+bμ2,a2σ12+b2σ22)
重参数化技巧 (数3)
设标准高斯分布
N
(
0
,
1
)
N(0, 1)
N(0,1)随机采样的样本为
z
z
z,高斯分布
N
(
μ
,
σ
2
)
N(\mu, \sigma^2)
N(μ,σ2)随机采样的样本表示为
z
′
z'
z′。使用重参数化技巧,可以将
z
′
z'
z′表示为:
z
′
=
σ
z
+
μ
z' = \sigma z + \mu
z′=σz+μ
贝叶斯公式 (数4)
p ( A ∣ B ) = p ( B ∣ A ) p ( A ) p ( B ) p(A|B) = p(B|A)\frac{p(A)}{p(B)} p(A∣B)=p(B∣A)p(B)p(A)
指数乘除法 (数5)
e x p ( a ) ∗ e x p ( b ) / e x p ( c ) = e x p ( a + b − c ) exp(a) * exp(b) / exp(c) = exp(a+b-c) exp(a)∗exp(b)/exp(c)=exp(a+b−c)
扩散过程
给定初始分布
x
0
∼
q
(
x
)
x_0\sim q(x)
x0∼q(x)(其中
x
0
x_0
x0代表某各训练样本,
q
(
x
)
q(x)
q(x)代表训练数据集分布),可以不断向其中加入高斯噪声。规定此策略为:在
t
t
t时刻,对
x
t
−
1
x_{t-1}
xt−1进行
1
−
β
t
\sqrt{1 - \beta_t}
1−βt倍的数值缩放,并向其中加入
β
t
\beta_t
βt倍标准高斯噪声
z
t
−
1
z_{t-1}
zt−1得到数据
x
t
x_t
xt。此过程表示为:
x
t
=
1
−
β
t
x
t
−
1
+
β
t
z
t
−
1
(
1
)
x_t = \sqrt{1-\beta_t}x_{t-1} +\sqrt{\beta_t}z_{t-1} \ \ \ (1)
xt=1−βtxt−1+βtzt−1 (1)
随着t不断增大,最终达到T时,样本数据(
x
T
x_T
xT)成了一个各项独立的高斯分布。且由于策略已知,
x
T
x_T
xT能通过迭代计算求得。为了节约计算资源并为一些后续工作做准备,可以通过公式推导求得
x
t
x_t
xt和
x
0
x_0
x0之间的关系,这使得任意时刻的
x
t
x_t
xt能通过公式一步求得。具体公式推导如下:
为方便表示,令
α
t
=
1
−
β
t
\alpha_t = 1-\beta_t
αt=1−βt,
α
ˉ
t
=
∏
i
=
1
T
α
i
\bar{\alpha}_t=\prod^{T}_{i=1}\alpha_i
αˉt=∏i=1Tαi。要求给定
x
t
−
1
x_{t-1}
xt−1情况下
x
t
x_t
xt的分布函数
q
(
x
t
∣
x
t
−
1
)
q(x_t|x_{t-1})
q(xt∣xt−1)。由(1)和(数3)进行比对可得:
q
(
x
t
∣
x
t
−
1
)
=
N
(
1
−
β
t
x
t
−
1
,
β
t
)
(
2
)
=
N
(
α
t
x
t
−
1
,
1
−
α
t
)
(
3
)
\begin{aligned} q(x_t|x_{t-1}) &= N(\sqrt{1-\beta_t}x_{t-1},\beta_t) \ (2)\\ &=N(\sqrt{\alpha_t}x_{t-1}, 1-\alpha_t) \ (3) \\ \end{aligned}
q(xt∣xt−1)=N(1−βtxt−1,βt) (2)=N(αtxt−1,1−αt) (3)
对
x
t
x_t
xt进行递归拆解:
x
t
=
α
t
x
t
−
1
+
1
−
α
t
z
t
−
1
(
5
)
w
h
e
r
e
z
t
−
1
,
z
t
−
2
,
.
.
.
,
z
∼
N
(
0
,
1
)
=
α
t
(
α
t
−
1
x
t
−
2
+
1
−
α
t
−
1
z
t
−
2
)
+
1
−
α
t
z
t
−
1
(
6
)
=
α
t
α
t
−
1
x
t
−
2
+
α
t
−
α
t
α
t
−
1
z
t
−
2
+
1
−
α
t
z
t
−
1
(
7
)
=
α
t
α
t
−
1
x
t
−
2
+
1
−
α
t
α
t
−
1
z
t
−
2
(
8
)
=
.
.
.
=
α
ˉ
t
x
0
+
1
−
α
ˉ
t
z
(
9
)
\begin{aligned} x_t &= \sqrt{\alpha_t}x_{t-1} + \sqrt{1-\alpha_t}z_{t-1} \ (5) \ \ \ where\ z_{t-1},z_{t-2},...,z \sim N(0,1)\\ &=\sqrt{\alpha_t}(\sqrt{\alpha_{t-1}}x_{t-2} + \sqrt{1-\alpha_{t-1}}z_{t-2} ) + \sqrt{1-\alpha_t}z_{t-1} \ (6)\\ &=\sqrt{\alpha_t\alpha_{t-1}}x_{t-2}+\sqrt{\alpha_t-\alpha_t\alpha_{t-1}}z_{t-2}+ \sqrt{1-\alpha_t}z_{t-1} \ (7) \\ &=\sqrt{\alpha_t\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_t\alpha_{t-1}}z_{t-2} \ (8) \\ &=... \\ &= \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1 - \bar{\alpha}_t}z \ (9) \end{aligned}
xt=αtxt−1+1−αtzt−1 (5) where zt−1,zt−2,...,z∼N(0,1)=αt(αt−1xt−2+1−αt−1zt−2)+1−αtzt−1 (6)=αtαt−1xt−2+αt−αtαt−1zt−2+1−αtzt−1 (7)=αtαt−1xt−2+1−αtαt−1zt−2 (8)=...=αˉtx0+1−αˉtz (9)
式(7)到式(8)的解释:
由(数3)及(数2)可知,
α
t
−
α
t
α
t
−
1
z
t
−
2
+
1
−
α
t
z
t
−
1
\sqrt{\alpha_t-\alpha_t\alpha_{t-1}}z_{t-2}+ \sqrt{1-\alpha_t}z_{t-1}
αt−αtαt−1zt−2+1−αtzt−1可重参数化为一个只含标准高斯
z
z
z的
1
−
α
t
α
t
−
1
z
\sqrt{1-\alpha_t\alpha_{t-1}}z
1−αtαt−1z,又因为
z
t
−
2
,
z
z_{t-2}, z
zt−2,z都是标准高斯,进行等效替换后为
1
−
α
t
α
t
−
1
z
t
−
2
\sqrt{1-\alpha_t\alpha_{t-1}}z_{t-2}
1−αtαt−1zt−2。
逆扩散过程
如果你已经能理解上一节的内容,那祝贺你拥有非凡的语文阅读能力及数学理解能力。这一节的内容可能略难,我对自己的表达能力与数学水平并不是很自信,但拥有如此理解能力的你想必也能轻松阅读这一节,让我们开始吧。
故名思意,逆扩散过程必定是扩散过程的反过程。在上一节中,我们成功求出了
q
(
x
t
∣
x
t
−
1
)
q(x_t|x_{t-1})
q(xt∣xt−1)的表达式,这使得我们可以轻松求得任何扩散时刻下的结果。同样,如果我们在逆过程中能求得
q
(
x
t
−
1
∣
x
t
)
q(x_{t-1}|x_{t})
q(xt−1∣xt)的表达式,这个逆过程也将成为我们的囊中之物。下面让我们开始吧:
q
(
x
t
−
1
∣
x
t
)
=
q
(
x
t
∣
x
t
−
1
)
∗
q
(
x
t
−
1
)
q
(
x
t
)
(
10
)
.
.
.
由
(
数
4
)
可知
=
(
α
t
x
t
−
1
+
1
−
α
t
z
t
−
1
)
∗
α
ˉ
t
−
1
x
0
+
1
−
α
ˉ
t
−
1
z
α
ˉ
t
x
0
+
1
−
α
ˉ
t
z
(
11
)
.
.
.
由
(
5
)
,
(
9
)
可知
=
(
α
t
x
t
−
1
+
β
t
z
t
−
1
)
∗
α
ˉ
t
−
1
x
0
+
1
−
α
ˉ
t
−
1
z
α
ˉ
t
x
0
+
1
−
α
ˉ
t
z
(
12
)
∝
e
x
p
(
−
(
x
t
−
α
t
x
t
−
1
)
2
2
β
t
)
∗
e
x
p
(
−
(
x
t
−
1
−
α
ˉ
t
−
1
x
0
)
2
2
(
1
−
α
ˉ
t
−
1
)
)
/
e
x
p
(
−
(
x
t
−
α
ˉ
t
x
0
)
2
2
(
1
−
α
ˉ
t
)
)
(
13
)
.
.
.
由
(
数
3
)
,
(
数
1
)
可知
=
e
x
p
[
−
1
2
(
(
x
t
−
α
t
x
t
−
1
)
2
β
t
+
(
x
t
−
1
−
α
ˉ
t
−
1
x
0
)
2
1
−
α
ˉ
t
−
1
−
(
x
t
−
α
ˉ
t
x
0
)
2
1
−
α
ˉ
t
)
]
(
14
)
.
.
.
由
(
数
5
)
可知
=
e
x
p
[
−
1
2
(
x
t
2
−
2
α
t
x
t
x
t
−
1
+
α
t
x
t
−
1
2
β
t
+
x
t
−
1
2
−
2
α
ˉ
t
−
1
x
0
x
t
−
1
+
α
ˉ
t
−
1
x
0
2
1
−
α
ˉ
t
−
1
−
(
x
t
−
α
ˉ
t
x
0
)
2
1
−
α
ˉ
t
)
]
(
15
)
=
e
x
p
[
−
1
2
(
(
α
t
β
t
+
1
1
−
α
ˉ
t
−
1
)
x
t
−
1
2
−
(
2
α
t
β
t
x
t
+
2
α
ˉ
t
−
1
1
−
α
ˉ
t
−
1
x
0
)
x
t
−
1
+
C
)
]
(
16
)
.
.
.
由于
x
0
,
x
t
不含
x
t
−
1
项被整合为常数
C
\begin{aligned} q(x_{t-1}|x_{t}) &= q(x_t|x_{t-1}) * \frac{q(x_{t-1})}{q(x_t)} \ \ (10) \ \ \ ...由(数4)可知\\ &=(\sqrt{\alpha_t}x_{t-1} + \sqrt{1-\alpha_t}z_{t-1}) *\frac{ \sqrt{\bar{\alpha}_{t-1}}x_0 + \sqrt{1 - \bar{\alpha}_{t-1}}z}{ \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1 - \bar{\alpha}_t}z} \ \ (11) \ \ \ ...由(5),(9)可知\\ &=(\sqrt{\alpha_t}x_{t-1} + \sqrt{\beta_t}z_{t-1}) *\frac{ \sqrt{\bar{\alpha}_{t-1}}x_0 + \sqrt{1 - \bar{\alpha}_{t-1}}z}{ \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1 - \bar{\alpha}_t}z} \ \ (12) \\ &\propto exp(-\frac{(x_t-\sqrt{\alpha_t}x_{t-1})^2}{2\beta_t}) * exp(-\frac{(x_{t-1}-\sqrt{\bar{\alpha}_{t-1}}x_0)^2}{2(1- \bar{\alpha}_{t-1})}) / exp(-\frac{(x_{t}-\sqrt{\bar{\alpha}_{t}}x_0)^2}{2(1- \bar{\alpha}_{t})}) \ \ (13) \ \ \ ...由(数3),(数1)可知\\ &= exp[-\frac{1}{2}(\frac{(x_t-\sqrt\alpha_t x_{t-1})^2}{\beta_t}+\frac{(x_{t-1}-\sqrt{\bar{\alpha}_{t-1}} x_{0})^2}{1-\bar{\alpha}_{t-1} }-\frac{(x_{t}-\sqrt{\bar{\alpha}_t} x_{0})^2}{1-\bar{\alpha}_{t} })] \ \ (14) \ \ \ ...由(数5)可知\\ &=exp[-\frac{1}{2}(\frac{x_t^2-2\sqrt\alpha_tx_t x_{t-1}+\alpha_tx_{t-1}^2}{\beta_t}+\frac{x_{t-1}^2-2\sqrt{\bar{\alpha}_{t-1}} x_{0}x_{t-1}+\bar{\alpha}_{t-1}x_0^2}{1-\bar{\alpha}_{t-1} }-\frac{(x_{t}-\sqrt{\bar{\alpha}_t} x_{0})^2}{1-\bar{\alpha}_{t} })] \ \ (15) \\ &=exp[-\frac{1}{2}((\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}_{t-1}})x_{t-1}^2-(\frac{2\sqrt\alpha_t}{\beta_t}x_t+\frac{2\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}}x_0)x_{t-1} +C)]\ \ (16) \ \ ...由于x_0,x_t不含x_{t-1}项被整合为常数C\\ \end{aligned}
q(xt−1∣xt)=q(xt∣xt−1)∗q(xt)q(xt−1) (10) ...由(数4)可知=(αtxt−1+1−αtzt−1)∗αˉtx0+1−αˉtzαˉt−1x0+1−αˉt−1z (11) ...由(5),(9)可知=(αtxt−1+βtzt−1)∗αˉtx0+1−αˉtzαˉt−1x0+1−αˉt−1z (12)∝exp(−2βt(xt−αtxt−1)2)∗exp(−2(1−αˉt−1)(xt−1−αˉt−1x0)2)/exp(−2(1−αˉt)(xt−αˉtx0)2) (13) ...由(数3),(数1)可知=exp[−21(βt(xt−αtxt−1)2+1−αˉt−1(xt−1−αˉt−1x0)2−1−αˉt(xt−αˉtx0)2)] (14) ...由(数5)可知=exp[−21(βtxt2−2αtxtxt−1+αtxt−12+1−αˉt−1xt−12−2αˉt−1x0xt−1+αˉt−1x02−1−αˉt(xt−αˉtx0)2)] (15)=exp[−21((βtαt+1−αˉt−11)xt−12−(βt2αtxt+1−αˉt−12αˉt−1x0)xt−1+C)] (16) ...由于x0,xt不含xt−1项被整合为常数C
与(数1)公式进行对比,可知:
α
t
β
t
+
1
1
−
α
ˉ
t
−
1
⇔
1
σ
2
(
17
)
2
α
t
β
t
x
t
+
2
α
ˉ
t
−
1
1
−
α
ˉ
t
−
1
x
0
⇔
2
μ
σ
2
(
18
)
q
(
x
t
−
1
∣
x
t
)
=
N
(
μ
,
σ
)
\begin{aligned} \frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}_{t-1}}&\Leftrightarrow \frac{1}{\sigma^2} \ \ (17) \\ \\ \frac{2\sqrt\alpha_t}{\beta_t}x_t+\frac{2\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}}x_0&\Leftrightarrow\frac{2\mu}{\sigma^2} \ \ (18)\\ \\ q(x_{t-1}|x_{t}) &=N(\mu, \sigma) \end{aligned}
βtαt+1−αˉt−11βt2αtxt+1−αˉt−12αˉt−1x0q(xt−1∣xt)⇔σ21 (17)⇔σ22μ (18)=N(μ,σ)
将(17)带入(18)得:
α
t
β
t
x
t
+
α
ˉ
t
−
1
1
−
α
ˉ
t
−
1
x
0
=
(
α
t
β
t
+
1
1
−
α
ˉ
t
−
1
)
μ
(
19
)
\frac{\sqrt\alpha_t}{\beta_t}x_t+\frac{\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}}x_0=(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}_{t-1}}){\mu} \ \ (19)
βtαtxt+1−αˉt−1αˉt−1x0=(βtαt+1−αˉt−11)μ (19)
进行整理得:
μ
=
α
t
β
t
x
t
+
α
ˉ
t
−
1
1
−
α
ˉ
t
−
1
x
0
α
t
β
t
+
1
1
−
α
ˉ
t
−
1
(
20
)
=
(
1
−
α
ˉ
t
−
1
)
α
t
x
t
+
β
t
α
ˉ
t
−
1
x
0
(
1
−
α
ˉ
t
−
1
)
α
t
+
β
t
=
(
1
−
α
ˉ
t
−
1
)
α
t
x
t
+
β
t
α
ˉ
t
−
1
x
0
α
t
−
α
ˉ
t
−
1
α
t
+
1
−
α
t
(
21
)
=
(
1
−
α
ˉ
t
−
1
)
α
t
x
t
+
β
t
α
ˉ
t
−
1
x
0
1
−
α
ˉ
t
−
1
α
t
(
22
)
=
(
1
−
α
ˉ
t
−
1
)
α
t
x
t
+
β
t
α
ˉ
t
−
1
x
0
1
−
α
ˉ
t
(
23
)
\begin{aligned} \mu &= \frac{\frac{\sqrt\alpha_t}{\beta_t}x_t+\frac{\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}}x_0}{\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}_{t-1}}} \ \ (20) \\ &=\frac{(1-\bar{\alpha}_{t-1})\sqrt{\alpha_t}x_t+\beta_t\sqrt{\bar{\alpha}_{t-1}}x_0}{(1-\bar{\alpha}_{t-1})\alpha_t+\beta_t} \\ &=\frac{(1-\bar{\alpha}_{t-1})\sqrt{\alpha_t}x_t+\beta_t\sqrt{\bar{\alpha}_{t-1}}x_0}{\alpha_t-\bar{\alpha}_{t-1}\alpha_t+1-\alpha_t} \ \ (21) \\ &= \frac{(1-\bar{\alpha}_{t-1})\sqrt{\alpha_t}x_t+\beta_t\sqrt{\bar{\alpha}_{t-1}}x_0}{1-\bar{\alpha}_{t-1}\alpha_t} \ \ (22) \\ &=\frac{(1-\bar{\alpha}_{t-1})\sqrt{\alpha_t}x_t+\beta_t\sqrt{\bar{\alpha}_{t-1}}x_0}{1-\bar{\alpha}_{t}} \ \ (23) \end{aligned}
μ=βtαt+1−αˉt−11βtαtxt+1−αˉt−1αˉt−1x0 (20)=(1−αˉt−1)αt+βt(1−αˉt−1)αtxt+βtαˉt−1x0=αt−αˉt−1αt+1−αt(1−αˉt−1)αtxt+βtαˉt−1x0 (21)=1−αˉt−1αt(1−αˉt−1)αtxt+βtαˉt−1x0 (22)=1−αˉt(1−αˉt−1)αtxt+βtαˉt−1x0 (23)
将(9)变形得
x
0
=
1
α
ˉ
t
(
x
t
−
1
−
α
ˉ
t
z
)
x_0 = \frac{1}{\sqrt{\bar\alpha_t}}(x_t-\sqrt{1-\bar{\alpha}_t}z)
x0=αˉt1(xt−1−αˉtz),(23)中可用
x
t
x_t
xt代替
x
0
x_0
x0变为:
μ
=
(
1
−
α
ˉ
t
−
1
)
α
t
x
t
+
β
t
α
ˉ
t
−
1
1
α
ˉ
t
(
x
t
−
1
−
α
ˉ
t
z
)
1
−
α
ˉ
t
(
24
)
=
(
1
−
α
ˉ
t
−
1
)
α
t
x
t
+
β
t
1
α
t
(
x
t
−
1
−
α
ˉ
t
z
)
1
−
α
ˉ
t
(
25
)
=
(
1
−
α
ˉ
t
−
1
)
α
t
x
t
+
β
t
(
x
t
−
1
−
α
ˉ
t
z
)
(
1
−
α
ˉ
t
)
α
t
(
26
)
=
(
1
−
α
ˉ
t
−
1
)
α
t
+
β
t
(
1
−
α
ˉ
t
)
α
t
x
t
−
β
t
1
−
α
ˉ
t
(
1
−
α
ˉ
t
)
α
t
z
(
27
)
=
1
a
t
(
(
1
−
α
ˉ
t
−
1
)
α
t
+
β
t
1
−
α
ˉ
t
x
t
−
β
t
1
−
α
ˉ
t
1
−
α
ˉ
t
z
)
(
28
)
=
1
a
t
(
α
t
−
α
ˉ
t
+
1
−
α
t
1
−
α
ˉ
t
x
t
−
β
t
1
−
α
ˉ
t
z
)
(
29
)
=
1
a
t
(
1
−
α
ˉ
t
1
−
α
ˉ
t
x
t
−
β
t
1
−
α
ˉ
t
z
)
(
30
)
=
1
a
t
(
x
t
−
β
t
1
−
α
ˉ
t
z
)
(
31
)
\begin{aligned} \mu &=\frac{(1-\bar{\alpha}_{t-1})\sqrt{\alpha_t}x_t+\beta_t\sqrt{\bar{\alpha}_{t-1}} \frac{1}{\sqrt{\bar\alpha_t}}(x_t-\sqrt{1-\bar{\alpha}_t}z)}{1-\bar{\alpha}_{t}} \ \ (24)\\ &=\frac{(1-\bar{\alpha}_{t-1})\sqrt{\alpha_t}x_t+\beta_t\frac{1}{\sqrt{\alpha_t}}(x_t-\sqrt{1-\bar{\alpha}_t}z)}{1-\bar{\alpha}_{t}} \ \ (25)\\ &=\frac{(1-\bar{\alpha}_{t-1}){\alpha_t}x_t+\beta_t(x_t-\sqrt{1-\bar{\alpha}_t}z)}{(1-\bar{\alpha}_{t})\sqrt{\alpha_t}} \ \ (26)\\ &=\frac{(1-\bar{\alpha}_{t-1}){\alpha_t}+\beta_t }{(1-\bar{\alpha}_{t})\sqrt{\alpha_t}}x_t - \frac{\beta_t\sqrt{1-\bar{\alpha}_t}}{(1-\bar{\alpha}_{t})\sqrt{\alpha_t}}z\ \ (27) \\ &=\frac{1}{\sqrt{a_t}}(\frac{(1-\bar{\alpha}_{t-1}){\alpha_t}+\beta_t }{1-\bar{\alpha}_{t}}x_t - \frac{\beta_t\sqrt{1-\bar{\alpha}_t}}{1-\bar{\alpha}_{t}}z)\ \ (28) \\ &=\frac{1}{\sqrt{a_t}}(\frac{\alpha_t-\bar{\alpha}_{t}+1-\alpha_t }{1-\bar{\alpha}_{t}}x_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_{t}}}z)\ \ (29) \\ &=\frac{1}{\sqrt{a_t}}(\frac{1-\bar{\alpha}_{t}}{1-\bar{\alpha}_{t}}x_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_{t}}}z) \ \ (30)\\ &=\frac{1}{\sqrt{a_t}}(x_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_{t}}}z)\ \ (31) \\ \end{aligned}
μ=1−αˉt(1−αˉt−1)αtxt+βtαˉt−1αˉt1(xt−1−αˉtz) (24)=1−αˉt(1−αˉt−1)αtxt+βtαt1(xt−1−αˉtz) (25)=(1−αˉt)αt(1−αˉt−1)αtxt+βt(xt−1−αˉtz) (26)=(1−αˉt)αt(1−αˉt−1)αt+βtxt−(1−αˉt)αtβt1−αˉtz (27)=at1(1−αˉt(1−αˉt−1)αt+βtxt−1−αˉtβt1−αˉtz) (28)=at1(1−αˉtαt−αˉt+1−αtxt−1−αˉtβtz) (29)=at1(1−αˉt1−αˉtxt−1−αˉtβtz) (30)=at1(xt−1−αˉtβtz) (31)
σ
\sigma
σ的求解更为简单,直接对(17)进行变形即可:
1
σ
2
=
α
t
(
1
−
α
ˉ
t
−
1
)
+
β
t
β
t
(
1
−
α
ˉ
t
−
1
)
(
32
)
σ
2
=
β
t
(
1
−
α
ˉ
t
−
1
)
α
t
(
1
−
α
ˉ
t
−
1
)
+
β
t
(
33
)
≈
β
t
α
t
+
β
t
=
β
t
(
34
)
.
.
.
由
α
t
=
1
−
β
t
可知
σ
=
β
t
(
35
)
\begin{aligned} \frac{1}{\sigma^2} &= \frac{\alpha_t(1-\bar{\alpha}_{t-1})+\beta_t}{\beta_t(1-\bar{\alpha}_{t-1})} \ \ (32)\\ \sigma^2 &= \frac{\beta_t(1-\bar{\alpha}_{t-1})}{\alpha_t(1-\bar{\alpha}_{t-1})+\beta_t} \ \ (33) \\ &\approx \frac{\beta_t}{\alpha_t+\beta_t} = \beta_t \ \ (34) \ \ \ ...由\alpha_t=1-\beta_t可知 \\ \sigma&=\sqrt{\beta_t} \ \ \ (35) \end{aligned}
σ21σ2σ=βt(1−αˉt−1)αt(1−αˉt−1)+βt (32)=αt(1−αˉt−1)+βtβt(1−αˉt−1) (33)≈αt+βtβt=βt (34) ...由αt=1−βt可知=βt (35)
由于
0
<
α
t
<
1
0<\alpha_t<1
0<αt<1,当t足够大有
α
ˉ
t
≈
0
\bar{\alpha}_t \approx 0
αˉt≈0,所以(33)到(34)公式成立。
如果
μ
,
σ
\mu,\sigma
μ,σ表达式已知,则条件概率分布
q
(
x
t
−
1
∣
x
t
)
=
N
(
μ
,
σ
)
q(x_{t-1}|x_{t})=N(\mu,\sigma)
q(xt−1∣xt)=N(μ,σ)已知,使得我们从一个随机高斯样本
x
t
x_t
xt通过循环迭代能求得符合真实数据分布的样本
x
0
x_0
x0。
事实上,我们离上诉描述已经很接近了,但在
μ
\mu
μ的表达式中,我们存在唯一一个未知量,这就是
z
z
z。在训练时由于策略已知,
z
z
z可以人为是已知量。但在推理阶段,减噪声策略未知,
z
z
z被视为未知量。此时,神经网络出场了。在训练阶段,我们只需训练一个模型用来预测
z
′
z'
z′,通过与已知的
z
z
z做损失对比,完成训练后,使用此网络来求得一系列的
z
′
z'
z′就能完成整个逆扩散过程。根据论文,模型的输入被定义为
x
t
和
t
x_t和t
xt和t,损失函数则可表示为下式:
L
simple
=
E
t
,
x
t
,
z
[
∥
z
−
ϵ
θ
(
x
t
,
t
)
∥
2
]
=
E
t
,
x
0
,
z
[
∥
z
−
ϵ
θ
(
α
ˉ
t
x
0
+
1
−
α
ˉ
t
z
,
t
)
∥
2
]
\begin{aligned} \mathcal{L}_{\text{simple}} &=\mathbb{E}_{t, \mathbf{x}_{t},z}\left[ \Vert z- \epsilon_{\theta}(x_t, t) \Vert^{2} \right] \\ &=\mathbb{E}_{t, \mathbf{x}_{0},z}\left[ \Vert z - \epsilon_{\theta}(\sqrt{\bar{\alpha}_{t}}x_{0} + \sqrt{1 - \bar{\alpha}_{t}}z, t) \Vert^{2} \right] \end{aligned}
Lsimple=Et,xt,z[∥z−ϵθ(xt,t)∥2]=Et,x0,z[∥z−ϵθ(αˉtx0+1−αˉtz,t)∥2]
至此,我们的扩散过程与逆扩散过程可被公式完整表达(其中
z
z
z表示随机高斯采样):
正向:
x
t
=
α
ˉ
t
x
0
+
1
−
α
ˉ
t
z
x_t = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1 - \bar{\alpha}_t}z \
xt=αˉtx0+1−αˉtz
逆向:
x
t
−
1
=
1
α
t
(
x
t
−
1
−
α
t
1
−
α
t
ˉ
ϵ
θ
(
x
t
,
t
)
)
+
β
t
z
x_{t-1} = \frac{1}{\sqrt{\alpha_{t}}}(x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha_t}}}\epsilon_{\theta}(x_t, t)) + \sqrt{\beta_t} z \
xt−1=αt1(xt−1−αtˉ1−αtϵθ(xt,t))+βtz
代码
https://colab.research.google.com/drive/179Se6GXKB30RQnVt7uqvS-vKsBQnRAee
参考链接
https://t.bilibili.com/700526762586538024?spm_id_from=333.999.0.0
https://zhuanlan.zhihu.com/p/586362713




















 3774
3774











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








