Bernouli Distribution(中文翻译称伯努利分布)
该分布研究的是一种特殊的实验,这种实验只有两个结果要么成功要么失败,且每次实验是独立的并每次实验都有固定的成功概率p。
概率公式可以表示为 
根据数学期望的性质
由于这里x只有两个取值所以该分布的数学期望为
方差则可以由方差公式来计算
方差公式:
该分布显然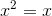

所以方差
最后我们来推导该分布的最大似然估计
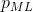
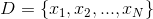
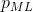
由于0<p<1,要使上面的式子最大,等价于使加上ln底的式子值最大,我们加上ln的底就可以将连乘转换为加和的形式,推导公式如下
再由最大似然方程可知,要选取p使该式子最大,则只要使该式对p进行求导的值为0,即
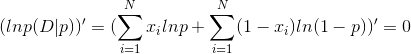
化简后我们最终求得









 本文深入探讨了伯努利分布的基本性质,包括数学期望、方差的计算方法,以及如何通过最大似然估计找到最可能的概率值。通过解析公式和实例,清晰展示了伯努利分布在概率论中的应用。
本文深入探讨了伯努利分布的基本性质,包括数学期望、方差的计算方法,以及如何通过最大似然估计找到最可能的概率值。通过解析公式和实例,清晰展示了伯努利分布在概率论中的应用。
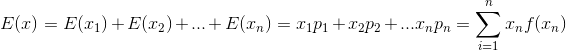
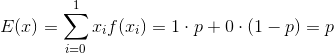
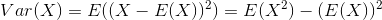
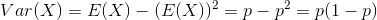
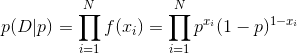
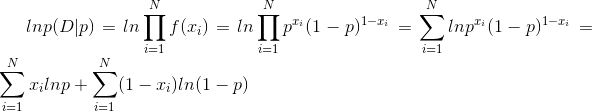
















 4048
4048

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








